Урок 26. Деление суммы на число. Страница 71
7. Лыжник должен пройти 132 км. Он шел 3 дня, проходя по 35 км в день. Сколько километров ему осталось пройти?
Решение:
1) 35 * 3 = (30 + 5) * 3 = 30 * 3 + 5 * 3 = 90 + 15 = 105 (км) − прошел лыжник за 3 часа;
2) 132 − 105 = 27 (км) − осталось пройти лыжнику.
Ответ: 27 км.
8. Туристы отправились в поход. В первый день они прошли 12 км, во второй − на 4 км больше, чем в первый, а в третий день − в 4 раза меньше, чем в первый и во второй дни вместе. Сколько километров прошли туристы за эти три дня?
Решение:
1) 12 + 4 = 16 (км) - туристы прошли во второй день,
2) 12 + 16 = 28 (км) - прошли за первые два дня,
3) 28 : 4 = 7 (км) - прошли в третий день,
4) 28 + 7 = 35 (км) - прошли за 3 дня.
Ответ: 35 км.
9. Определи, какой знак нужно поставить в окошко, чтобы получилось верное высказывание.
a * 3 ☐ 9 * a
n * 3 + n * 9 ☐ 12 * n
d − 24 ☐ d − 310
156 − m ☐ 152 − m
b : 27 ☐ b : 207
35 : c ☐ 125 : c
Решение
а*3 < 9*а
n*3+n*9 = 12*n
d-24 > d-310
156-m > 152-m
b:27 > b:207
35:с < 125:с
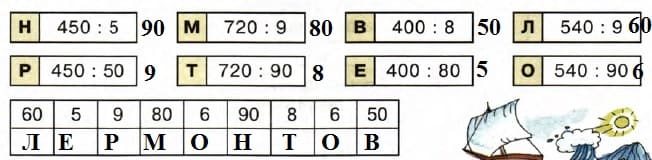
10. Вычисли. Расшифруй фамилию известного русского поэта. Узнай, в каком веке он жил.
Решение
Н = 450 : 5 = 45 д : 5 = 9 д = 90;
Р = 450 : 50 = 45 : 5 = 9;
М = 720 : 9 = 72 д : 9 = 8 д = 80;
Т = 720 : 90 = 72 : 9 = 8;
В = 400 : 8 = 40 д : 8 = 5 д = 50;
Е = 400 : 80 = 40 : 8 = 5;
Л = 540 : 9 = 54 д : 9 = 6 д = 60;
О = 540 : 90 = 54 : 9 = 6.
60 5 9 80 6 90 8 6 50
Л Е Р М О Н Т О В
Ответ: ЛЕРМОНТОВ. Он жил в 19 веке.
11. Найди значения выражений:
100 − 3 * 4 : 2 * 5
60 * 7 − 35 : 7 * 8 − 17
160 : (5 * 4) + (6 * 6 − 9)
(7 * 80 − 20) : 60 − 180 : 9 : 5
Решение
100 − 3 * 4 : 2 * 5 = 100 − 12 : 2 * 5 = 100 − 6 * 5 = 100 − 30 = 70
60 * 7 − 35 : 7 * 8 − 17 = 420 − 5 * 8 − 17 = 420 − 40 − 17 = 380 − 17 = 363
160 : (5 * 4) + (6 * 6 − 9) = 160 : 20 + (36 − 9) = 8 + 27 = 35
(7 * 80 − 20) : 60 − 180 : 9 : 5 = (560 − 20) : 60 − 20 : 5 = 540 : 60 − 4 = 9 − 4 = 5
12. Класс имеет форму прямоугольного параллелепипеда. Длина равна 10 м, ширина − 5 м, а высота − 3 м. Найди объем класса и площадь его стен.
Решение:
1) 10 * 5 * 3 = 10 * 15 = 150 $(м^3)$ − объем класса;
2) (10 * 3) * 2 + (5 * 3) * 2 = 6 * 10 + 3 * 10 = 60 + 30 = 90 $(м^2)$ − площадь стен.
Ответ: 150 $м^3$, 90 $м^2$.
13. Митя, Сережа, Юра, Толя и Костя пришли в музей до открытия и встали в очередь. Если бы Митя встал посредине очереди, он стоял бы между Сережей и Костей, а если бы в конце очереди, то рядом с ним стоял бы Юра. Но Митя встал впереди своих товарищей. Кто за кем стоит, если известно, что Костя стоит за Сережей?
Решение:
Значит Сережа и Костя уже стояли посредине и без Мити. При этом Юра стоит в самом конце, а значит Толя вначале. В итоге получается так: Митя, Толя, Сережа, Костя, Юра.