Урок 15. Умножение и деление на 10 и на 100. Страница 44
5. Реши уравнения с комментированием и сделай проверку:
мн. мн. пр.
х * 10 = 20,
х = 20 : 10,
х = 2.
Проверка:
2 * 10 = 20,
20 = 20.
мн. мн. пр.
10 * х = 800,
х = 800 : 10,
х = 80.
Проверка:
10 * 80 = 800,
800 = 800.
делим. делит. част.
х : 9 = 100,
х = 9 * 100,
х = 900.
Проверка:
900 : 9 = 100,
100 = 100.
делим. делит. част.
500 : х = 100,
х = 500 : 100,
х = 5.
Проверка:
500 : 5 = 100,
100 = 100.
6. Выполни действия.
100 * 10 = 1000
10 * 10 * 10 = 1000
1000 : 10 = 100
1000 : 100 = 10
7. Объясни по картинке смысл равенств в рамке.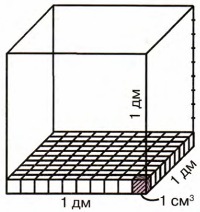
Решение
1 дм = 10 см
1) 1 дм * 1 дм * 1 дм = 1 $(дм^3)$ − объем куба в кубических дециметрах;
2) 10 см * 10 см * 10 см = 1000 $(см^3)$ − объем куба в кубических сантиметрах.
Поэтому:
1 $дм^3$ = 1000 $см^3$.
1 м = 10 дм
1) 1 м * 1 м * 1 м = 1 $(м^3)$ − объем куба в кубических метрах;
2) 10 дм * 10 дм * 10 дм = 1000 $(дм^3)$ − объем куба в кубических дециметрах.
Поэтому:
1 $м^3$ = 1000 $дм^3$.
8. Найди объем прямоугольного параллелепипеда, если известны все три его измерения (длина, ширина и высота):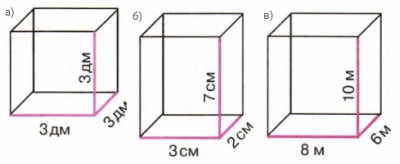
Решение
а) V = (a * b) * c = (3 * 3) * 3 = 9 * 3 = 27 $(дм^3)$ − объем прямоугольного параллелепипеда.
Ответ: 27 $дм^3$
б) V = (a * b) * c = (3 * 2) * 7 = 6 * 7 = 42 $(см^3)$ − объем прямоугольного параллелепипеда.
Ответ: 42 $см^3$
в) V = (a * b) * c = (8 * 6) * 10 = 48 * 10 = 480 $(м^3)$ − объем прямоугольного параллелепипеда.
Ответ: 480 $м^3$.
9. Запиши в виде произведения:
5 * 8 + 5
4 * 6 − 4
2 * 9 − 2 * 5
6 * 8 − 8 * 3
c * 3 + c * 4
a * 7 − 2 * a
n * 4 + n * 3 − n
$\underbrace{k + k + ... + k}_{35-раз}$
Решение
5 * 8 + 5 = 5 * 9;
4 * 6 − 4 = 4 * 5;
2 * 9 − 2 * 5 = 2 * 4;
6 * 8 − 8 * 3 = 8 * 3;
c * 3 + c * 4 = с * 7;
a * 7 − 2 * a = a * 5;
n * 4 + n * 3 − n = n * 6;
$\underbrace{k + k + ... + k}_{35-раз} = k * 35$.
10. Сравни...:
a * 8 ☐ a * 5 + a
b * 2 + b * 3 ☐ b * 7
d * 6 ☐ d * 7 − d
m + 3 * m ☐ m * 6 − m * 5
Решение
a * 5 + a = a * 6;
a * 8 > a * 6;
a * 8 > a * 5 + a.
b * 2 + b * 3 = b * 5;
b * 5 < b * 7;
b * 2 + b * 3 < b * 7.
d * 7 − d = d * 6;
d * 6 = d * 6;
d * 6 = d * 7 − d.
m + 3 * m = m * 4;
m * 6 − m * 5 = m * 1;
m * 4 > m * 1;
m + 3 * m > m * 6 − m * 5.
Краткая запись:
а * 8 > a * 5 + a
b * 2 + b * 3 < b * 7
d * 6 = d * 7 - d
m + 3 * m > m * 6 - m * 5

