Урок 16. Решение задач. Страница 47

6. По какому признаку выделены все числа первой строки? Найди по тому же признаку числа в остальных строках.  Выпиши в тетрадь все выделенные числа по строкам.  Сколько произведений из таблицы умножения чисел от 1 до 9 в каждом десятке? Выучи их.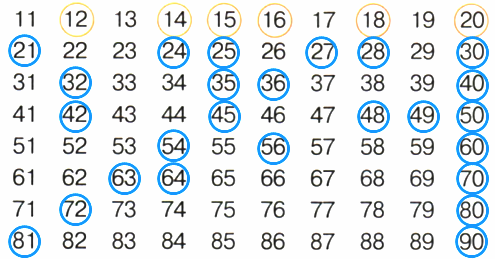

Ответ

Из вопроса внизу понятно, что авторы пытались собрать табличные значения для каждого десятка, то есть выписываем по факту числа из таблицы умножения.

В первой строке таблицы выделены числа, которые являются табличными произведениями.

Первый десяток:
1) 3 * 4 = 2 * 6 = 12
2) 2 * 7 = 14
3) 3 * 5 = 15
4) 4 * 4 = 16
5) 3 * 6 = 18
6) 2 * 10 = 20
Всего 6 табличных произведений.

Второй десяток:
1) 3 * 7 = 21
2) 4 * 6 = 24
3) 5 * 5 = 25
4) 3 * 9 = 27
5) 4 * 7 = 28
6) 3 * 10 = 30
Всего 6 табличных произведений.

Третий десяток:
1) 4 * 8 = 32
2) 5 * 7 = 35
3) 6 * 6 = 36
4) 4 * 10 = 40
Всего 4 табличных произведений.

Четвертый десяток:
1) 6 * 7 = 42
2) 5 * 9 = 45
3) 6 * 8 = 48
4) 7 * 7 = 49
5) 5 * 10 = 50
Всего 5 табличных произведений.

Пятый десяток:
1) 6 * 9 = 54
2) 7 * 8 = 56
3) 6 * 10 = 60
Всего 3 табличных произведения.

Шестой десяток:
1) 7 * 9 = 63
2) 8 * 8 = 64
3) 7 * 10 = 70
Всего 3 табличных произведения.

Седьмой десяток:
1) 8 * 9 = 72
2) 8 * 10 = 80
Всего 2 табличных произведения.

Восьмой десяток:
1) 9 * 9 = 81
2) 9 * 10 = 90
Всего 2 табличных произведения.

Выписываем:

12, 14, 15, 16, 18, 20
21, 24, 25, 27, 28, 30
32, 35, 36, 40
42, 45, 48, 49, 50
54, 56, 60
63, 64, 70
72, 80,
81, 90

7. Найди площадь закрашенных фигур: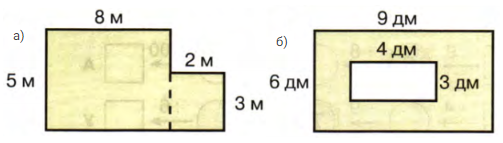

Решение

а. 1) 5 * 8 = 40 $(м^2)$ − площадь большого прямоугольника;
    2) 2 * 3 = 6 $(м^2)$ − площадь маленького прямоугольника;
    3) 40 + 6 = 46 $(м^2)$ − площадь закрашенной фигуры.
Ответ: 46 $м^2$.

б. 1) 9 * 6 = 54 $(дм^2)$ − площадь всей фигуры;
    2) 4 * 3 = 12 $(дм^2)$ − площадь незакрашенной фигуры;
    3) 54 − 12 = 42 $(дм^2)$ − площадь закрашенной фигуры.
Ответ: 42 $дм^2$.

8. Сравни...:
8 * 4 − 8 ☐ 5 * 8
29 * 7 ☐ 3 * 29
5 * 16 ☐ 16 + 16 * 4
4 м 32 см ☐ 423 см
308 см ☐ 3 м 8 дм
56 дм ☐ 5 м 6 см
20 $м^2$ ☐ 200 $дм^2$
54 $см^2$ ☐ 5 $дм^2$
800 $см^3$ ☐ 1 $дм^3$

Решение

8 * 4 − 8 = 8 * 3;
8 * 3 < 5 * 8;
8 * 4 − 8 < 5 * 8.

29 * 7 > 3 * 29

16 + 16 * 4 = 16 * 5;
5 * 16 = 16 * 5;
5 * 16 = 16 + 16 * 4.

4 м 32 см = (4 * 100 + 32) см = 432 см;
432 см > 423 см;
4 м 32 см > 423 см.

3 м 8 дм = (3 * 100 + 8 * 10) см = 380 см;
308 см < 380 см;
308 см < 3 м 8 дм.

5 м 6 см = 50 дм 6 см;
56 дм > 50 дм 6 см;
56 дм > 5 м 6 см.

20 $м^2$ = (20 * 100) $дм^2$ = 2000 $дм^2$;
2000 $дм^2$ > 200 $дм^2$;
20 $м^2$ > 200 $дм^2$.

5 $дм^2$ = (5 * 100) $см^2$ = 500 $см^2$;
54 $см^2$ < 500 $см^2$;
54 $см^2$ < 5 $дм^2$.

1 $дм^3$ = (1 * 1000) $см^3$ = 1000 $см^3$;
800 $см^3$ < 1000 $см^3$;
800 $см^3$ < 1 $дм^3$.

Короткая запись:

8 * 4 - 8 < 5*8
29 * 7 > 3 * 29
5 * 16 = 16 + 16 * 4

4 м 32 см > 423 см
308 см < 3 м 8 дм
56 дм > 5 м 6 см

20 м² > 200 дм²
54 см² < 5 дм²
800 см³ >1дм³

9. Прочитай свойства сложения и вычитания:

a + b = b + a − от перемены мест слагаемых сумма не изменяется;
(a + b) + c = a + (b + c) − чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел;
(a + b) − c = (a − с) + b − чтобы из суммы двух чисел вычесть третье число, можно из первого числа вычесть третье число и к результату прибавить второе число;
a − (b + c) = a − b − c − чтобы из числа вычесть сумму двух чисел, можно из первого числа последовательно вычесть второе и третье числа.

Используя эти свойства, вычисли устно:

(378 + 564) + 36
205 + (127 + 495)
(246 + 459) − 359
732 − 186 − 14

Решение

(378 + 564) + 36 = 378 + (564 + 36) = 378 + 600 = 978
205 + (127 + 495) = (205 + 495) + 127 = 700 + 127 = 827
(246 + 459) − 359 = (459 − 359) + 246 = 100 + 246 = 346
732 − 186 − 14 = 732 − (186 + 14) = 732 − 200 = 532