Ответы к теме "Повторение". Стр. 105

66. Найди объем прямоугольного параллелепипеда на рисунке, если объем каждого кубика равен 1 дм³.

Решение

1) 3 * 3 * 3 = 27 (кубиков) − объем прямоугольного параллелепипеда;
2) 27 * 1 = 27 (дм³) − объем прямоугольного параллелепипеда.
Ответ: 27 дм³.

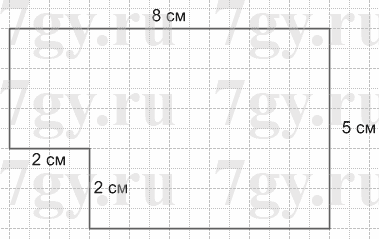
67. Длина прямоугольника равна 5 см, а ширина - 8 см. От одного из его углов отрезали квадрат со стороной 2 см. Построй получившуюся фигуру, найди ее периметр и площадь.

Решение

1) 5 * 8 = 40 (см²) − площадь прямоугольника;
2) 2 * 2 = 4 (см²) − площадь квадрата;
3) 40 − 4 = 36 (см²) − площадь фигуры;
4) 8 + 5 + (8 − 2) + (5 − 2) = 13 + 6 + 3 = 19 + 3 = 22 (см) − периметр фигуры.
Ответ: 22 см; 36 см².

68. Длина Толиной комнаты 5 м, ширина 4 м, а высота 3 м. Найди объем комнаты.

Решение

5 * 4 * 3 = 20 * 3 = 2 * 3 * 10 = 6 * 10 = 60 (м³) − объем комнаты.
Ответ: 60 м³.

69. Реши задачи двумя способами. Каким способом удобнее считать?
а) Около дома стояли 6 легковых автомобилей. Приехали еще 3 автомобиля. Сколько стало колес у машин, стоящих около этого дома?
б) В одной пачке 50 книг. На сколько количество книг в трех таких пачках меньше, чем в пяти таких пачках?

Решение

а) 6 * 4 + 3 * 4 = 24 + 12 = 36 (к.) − стало у машин, стоящих около этого дома;
    (6 + 3) * 4 = 9 * 4 = 36 (к.) − стало у машин, стоящих около этого дома.
    Ответ: 36 колес.

б)  50 * 5 − 50 * 3 = 250 − 150 = 100 (к.) − в трех таких пачках меньше, чем в пяти таких пачках;
      (5 − 3) * 50 = 2 * 50 = 100 (к.) − в трех таких пачках меньше, чем в пяти таких пачках.
       Ответ: на 100 книг.

Результаты первого и второго выражения равны по распределительному свойству умножения. Вторым способом считать легче.

70.  Вычисли наиболее простым способом:
(269 + 576) + 24
438 + 27 + 62 + 273
374 − (274 + 99)
(895 + 49) − 894
(93 * 5) * 2
(2 * 8) * (5 * 7)
48 * 15
35 * 28

Решение

(269 + 576) + 24 = (576 + 24) + 269 = 600 + 269 = 869

438 + 27 + 62 + 273 = (438 + 62) + (27 + 273) = 500 + 300 = 800

374 − (274 + 99) = (374 − 274) − 99 = 100 − 99 = 1

(895 + 49) − 894 = (895 − 894) + 49 = 1 + 49 = 50

(93 * 5) * 2 = 93 * (5 * 2) = 93 * 10 = 930

(2 * 8) * (5 * 7) = (8 * 7) * (5 * 2) = 56 * 10 = 560

48 * 15 = 2 * 24 * 5 * 3 = (24 * 3) * (2 * 5) = (20 + 4) * 3 * 10 = (20 * 3 + 4 * 3) * 10 = (60 + 12) * 10 = 72 * 10 = 720

35 * 28 = (7 * 5) * (2 * 14) = (14 * 7) * (2 * 5) = (10 + 4) * 7 * 10 = (10 * 7 + 4 * 7) * 10 = (70 + 28) * 10 = 98 * 10 = 980

71.  В эстафете приняли участие команды четырех школ, всего 244 ученика. В первой команде было 63 ученика, во второй − на 6 учеников меньше, чем в первой, а в третьей − в 2 раза меньше, чем в первой и второй командах вместе. Сколько учеников был в четвертой команде?

Решение

1) 63 − 6 = 57 (уч.) − было во второй команде;
2) 63 + 57 = 120 (уч.) − было в первых двух командах вместе;
3) 120 : 2 = 12 д : 2 = 6 д = 60 (уч.) − было в третьей команде;
4) 120 + 60 = 180 (уч.) − было в первых трех командах;
5) 244 − 180 = 64 (уч.) − было в четвертой команде.
Ответ: 64 ученика.

72.  Что общего в примерах каждого столбика? Вычисли и объясни прием вычислений.
19 * 10
100 * 6

80 * 7
30 * 20

19 * 4
8 * 53

68 : 2
75 : 3

84 : 28
91 : 13

38 : 9
45 : 7

Решение

19 * 10 = 190
100 * 6 = 600
В обоих примерах производится умножения на круглое число. Чтобы умножить число на 10, нужно к числу приписать справа один нуль, а если на 100, то два нуля.

80 * 7 = (8 * 7) * 10 = 56 * 10;
30 * 20 = (3 * 2) * (10 * 10) = 6 * 100 = 600.
В обоих примерах умножаются круглые числа. Чтобы умножить круглые числа, можно отбросить нули и выполнить умножение без них, а к произведению справа приписать отброшенные нули.

19 * 4 = (10 + 9) * 4 = 10 * 4 + 9 * 4 = 40 + 36 = 76;
8 * 53 = (50 + 3) * 8 = 50 * 8 + 3 * 8 = 400 + 24 = 424.
В обоих примерах используется умножение суммы на число. Чтобы умножить сумму на число, можно каждое слагаемое отдельно умножить на число и полученные произведения сложить.

68 : 2 = (60 + 8) : 2 = 60 : 2 + 8 : 2 = 30 + 4 = 34;
75 : 3 = (60 + 15) : 3 = 60 : 3 + 15 : 3 = 20 + 5 = 25.
В обоих примерах используется деление суммы на число. Чтобы разделить сумму на число, можно каждое слагаемое отдельно разделить на число и полученные произведения сложить.

84 : 28 = 3, так как 3 * 28 = (20 + 8) * 3 = 20 * 3 + 8 * 3 = 60 + 24 = 84;
91 : 13 = 7, так как 7 * 13 = (10 + 3) * 7 = 10 * 7 + 3 * 7 = 70 + 21 = 91.
В обоих примерах делится двузначное число на двузначное. При делении двузначного числа на двузначное можно найти частное подбором: это будет такое число, которое при умножении его на делитель даст в результате делимое.

38 : 9 = 4 (ост.2)
1) 36 − наибольшее число до 38, кратное 9;
2) 36 : 9 = 4 − частное;
3) 38 − 36 = 2 − остаток;
4) 2 < 9;
5) 9 * 4 + 2 = 36 + 2 = 38;
6) 38 : 9 = 4 (ост.2).

45 : 7 = 6 (ост.3)
1) 42 − наибольшее число до 45, кратное 7;
2) 42 : 7 = 6 − частное;
3) 45 − 42 = 3 − остаток;
4) 3 < 7;
5) 7 * 6 + 3 = 42 + 3 = 45;
6) 45 : 7 = 6 (ост.3).
В обоих примерах выполняется деление с остатком.