Ответы к странице учебника26

4. Назови центр окружности, ее радиусы и диаметр. Измерь радиусы и диаметр, сравни их. Что ты замечаешь?
AC = ... см;
DC = ... см;
BC = ... см;
KC = ... см;
AD = ... см.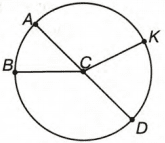

Решение

C − центр окружности;
AC, DC, BC, KC − радиусы окружности;
AD − диаметр окружности.
AC = 1 см;
DC = 1 см;
BC = 1 см;
KC = 1 см;
AD = 2 см.
Можно заметить, что все радиусы равны, а диаметр в 2 раза больше радиуса.

№5. Практическая работа
а) Начерти на листе бумаги циркулем окружность радиусом 5 см. Вырежи круг, ограниченный этой окружностью. Перегни его пополам, линию сгиба обведи карандашом. Повтори еще 2 раза по разным линиям сгиба. Что ты замечаешь?
б) Если при перегибании части фигур совпадают, то линию сгиба называют осью симметрии. Как её ещё можно назвать? Сколько осей симметрии имеют окружность, круг?

Решение

а) Можно заметить, что линии сгиба − это диаметры, которые пересекаются под прямым углом.
б) Еще можно назвать диаметром. Бесконечное множество осей симметрии.

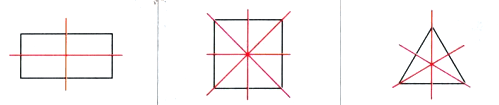
№6. Являются ли прямые на рисунке осями симметрии фигур? Проверь свою версию с помощью кальки. Найди перегибанием
все оси симметрии этих фигур.

Решение

Все прямые на рисунке являются осями симметрии фигур.
У прямоугольника 2 оси симметрии, у квадрата 4, у равностороннего треугольника 3.

№7. Перенеси в тетрадь и заполни таблицу:

8. Составь программу действий и вычисли:
(9 * 4) : 6 − 27 : (12 − 9) : 9
(35 + 7) : 6 * 8 + 28 : (16 − 9) * 9

Решение

   1     3    6     4       2     5
(9 * 4) : 6 − 27 : (12 − 9) : 9 = 36 : 6 − 27 : 3 : 9 = 6 − 9 : 9 = 6 − 1 = 5;
      1     3   4     7     5      2      6
(35 + 7) : 6 * 8 + 28 : (16 − 9) * 9 = 42 : 6 ∗ 8 + 28 : 7 ∗ 9 = 7 ∗ 8 + 4 ∗ 9 = 56 + 36 = 100