Урок 14. Объем фигуры. Страница 42.

4. Вычисли объем коробки с ребрами 3 дм, 2 дм и 2 дм двумя разными способами. Что ты замечаешь?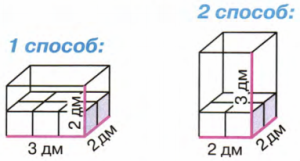

Решение

Способ 1.
V = (a * b) * c = (3 * 2) * 2 = 6 * 2 = 12 $(дм^3)$ − объем коробки.
Ответ: 12 $(дм^3)$

Способ 2.
V = (a * b) * c = (2 * 2) * 3 = 4 * 3 = 12 $(дм^3)$ − объем коробки.
Ответ: 12 $(дм^3)$

Можно заметить, что объем получился одинаковый.
Полученный результат объясняется тем, что коробка одна и та же, только в разном положении, а от перемены местами множителей произведение не меняется.

5. Дно коробки − квадрат со стороной 3 дм, а ее высота равна 5 дм. Сколько кубиков с ребром в 1 дм можно в нее положить?

Решение

У куба все стороны равны, поэтому:
1) 1 * 1 * 1 = 1 $(дм^3)$ − объем кубика;
У квадрата все стороны равны, поэтому:
2) 3 * 3 = 9 $(дм^2)$ − площадь дна коробки;
3) 9 * 5 = 45 $(дм^3)$ − объем коробки;
4) 45 : 1 = 45 (кубиков) − можно положить в коробку.
Ответ: 45 кубиков.

6. Коробка имеет длину 2 дм, ширину 4 дм, а высоту 3 дм. Чему равен объем коробки?

Решение

V = (a * b) * c = (2 * 4) * 3 = 8 * 3 = 24 $(дм^3)$ − объем коробки.
Ответ: 24 $дм^3$.

7. Найди числа, кратные 9, и запиши их в виде 9 * a:
19, 36, 49, 72, 45, 29, 63, 35, 54, 18, 90, 27, 81.

Решение

36 = 9 * 4
72 = 9 * 8
45 = 9 * 5
63 = 9 * 7
54 = 9 * 6
18 = 9 * 2
90 = 9 * 10
27 = 9 * 3
81 = 9 * 9

8. Составь программу действий и вычисли:
а) 81 : (11 − 2) * 8 + 9 * (14 : 2)
б) 7 * 8 − (5 * 6 − 12) : 3 − 49 : (7 * 7)
в) 0 * (6 + 3) + 4 : 4 * (15 − 3 * 2) − 0 : 8

а)   2   1    3   6  5   4
   81:(11-2)*8+9*(14:2)=81:9*8+9*7=72+63=135

б)   1  7  2   3    4  8  6  5
    7*8-(5*6-12):3-49:(7*7)=56-18:3-49:49=56-6-1=49

в)   2  1     7 6  5   4   3   9  8
    0*(6+3)+4:4*(15-3*2)-0:8=0+1*9-0=9

или по действиям:

а)
$81 \overset{3}{:} (11 \overset{1}{-} 2) \overset{4}{*} 8 \overset{6}{+} 9 \overset{5}{*} (14 \overset{2}{:} 2) = 81 : 9 * 8 + 9 * 7 = 9 * 8 + 63 = 72 + 63 = 135$
1) 11 − 2 = 9
2) 14 : 2 = 7
3) 81 : 9 = 9
4) 9 * 8 = 72
5) 9 * 7 = 63
6) 72 + 63 = 135

б)
$7 \overset{4}{*} 8 \overset{7}{-} (5 \overset{1}{*} 6 \overset{2}{-} 12) \overset{5}{:} 3 \overset{8}{-} 49 \overset{6}{:} (7 \overset{3}{*} 7) = 56 - (30 - 12) : 3 - 49 : 49 = 56 - 18 : 3 - 1 = 56 - 6 - 1 = 50 - 1 = 49$
1) 5 * 6 = 30
2) 30 − 12 = 18
3) 7 * 7 = 49
4) 7 * 8 = 56
5) 18 : 3 = 6
6) 49 : 49 = 1
7) 56 − 6 = 50
8) 50 − 1 = 49

в) 
$0 \overset{4}{*} (6 \overset{1}{+} 3) \overset{8}{+} 4 \overset{5}{:} 4 \overset{6}{*} (15 \overset{3}{-} 3 \overset{2}{*} 2) \overset{9}{-} 0 \overset{7}{:} 8 = 0 * 9 + 4 : 4 * (15 - 6) - 0 = 0 + 1 * 9 - 0 = 9$
1) 6 + 3 = 9
2) 3 * 2 = 6
3) 15 − 6 = 9
4) 0 * 9 = 0
5) 4 : 4 = 1
6) 1 * 9 = 9
7) 0 : 8 = 0
8) 0 + 9 = 0
9) 9 − 0 = 9

9. Найди пропущенные цифры и сделай проверку:

Решение

+342
  195
  537
Проверка:
1)
−537
  342
  195
2)
−537
  195
  342

−846
  217
  629
Проверка:
1)
−846
  629
  217
2)
+629
  217
  846

−870
  325
  545
Проверка:
1)
−870
  545
  325
2)
+325
  545
  870

+269
  442
  711
Проверка:
1)
−711
  269
  442
2)
−711
  442
  269

10. Вычисли наиболее удобным способом:
73 + (246 + 27)
64 + 209 + 36 + 71
(42 + 79) + (21 + 8)

Решение

73 + (246 + 27) = (73 + 27) + 246 = 100 + 246 = 346;
64 + 209 + 36 + 71 = (64 + 36) + (209 + 71) = 100 + 280 = 380;
(42 + 79) + (21 + 8) = (42 + 8) + (79 + 21) = 50 + 100 = 150.

11. Упрости выражения, используя свойства сложения:
a + 5 + 7       8 + 4 + b        6 + k + 9         8 + m + 7 + 2

Решение

a + 5 + 7 = a + (5 + 7) = a + 12
8 + 4 + b = b + (8 + 4) = b + 12
6 + k + 9 = k + (6 + 9) = k + 15
8 + m + 7 + 2 = m + (8 + 7 + 2) = m + 17

12. Сколькими способами можно разложить 5 одинаковых ручек в 2 разных пенала?

Решение

1) 0 + 5
2) 1 + 4
3) 2 + 3
4) 3 + 2
5) 4 + 1
6) 5 + 0
Ответ: возможны 6 способов.