Ответы к странице учебника 75
245.
Для правильного выполнения задания 245 учащиеся должны истолковать предложенную характеристику искомого числа, как логическую конструкцию, состоящую из трех частей и соединенную союзами «и». В свою очередь, это должно быть истолковано следующим образом: каждое из указанных трех условий должно быть выполнено для искомого числа. Если мы будем рассматривать шестизначные числа, которые меньше, чем число 100 010, то их будет всего десять: 100 009, 100 008, 100 007, …, 100 001 и 100 000. Среди них только последнее число является «круглым». Это число 100 000. Оно и будет искомым.
Ответ:
100 000.
246.
Задание 246 внешне похоже на предыдущее задание: в нем также нужно найти числа, которые удовлетворяют данной характеристике (данному характеристическому свойству). Принципиальное отличие состоит в том, что отдельные условия этого характеристического свойства связывает союз «или», а не союз «и», как это было в предыдущем задании. Логический смысл союза «или» говорит о том, что искомое число должно удовлетворять хотя бы одному из указанных требований: быть круглым двузначным или быть двузначным, которое меньше 15. Перечислим все такие числа: 10, 20, 30, 40, 50, 60, 70, 80, 90, 14, 13, 12, 11. Из всех этих чисел есть одно, которое удовлетворяет сразу двум данным требованиям. Это число 10. Оно и круглое двузначное, и двузначное, которое меньше 15. Но соединительный смысл союза «или» допускает такую возможность. Поэтому число 10 также входит в список искомых чисел.
Ответ:
10, 20, 30, 40, 50, 60, 70, 80, 90, 14, 13, 12, 11.
247.
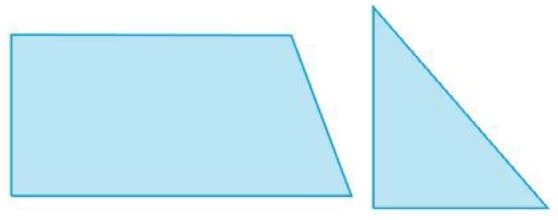
При выполнении задания 247 учащиеся столкнуться с характеристическим свойством геометрических фигур, которое с логической точки зрения состоит из двух частей, соединенных союзом «или». При этом каждая из указанных частей, в свою очередь, состоит из двух частей, соединенных союзом «и». Это означает, что сначала учащиеся могут отобрать те фигуры, которые удовлетворяют первой «половине» всего характеристического свойства, т. е. речь идет о фигурах, которые являются треугольниками и в них есть прямой угол. Фактически речь идет о прямоугольных треугольниках. После этого они должны к выбранным фигурам добавить те фигуры, которые удовлетворяют второй «половине» всего характеристического свойства, т. е. добавить четырехугольники, у которых есть прямой угол (добавить прямоугольную трапецию). Таким образом, невыбранными останутся три фигуры: остроугольный и тупоугольный треугольники (в них нет прямого угла) и пятиугольник с прямым углом (он не является ни треугольником, ни четырехугольником).
Ответ: