Ответы к странице учебника 109. Геометрические фигуры и их свойства (повторение)

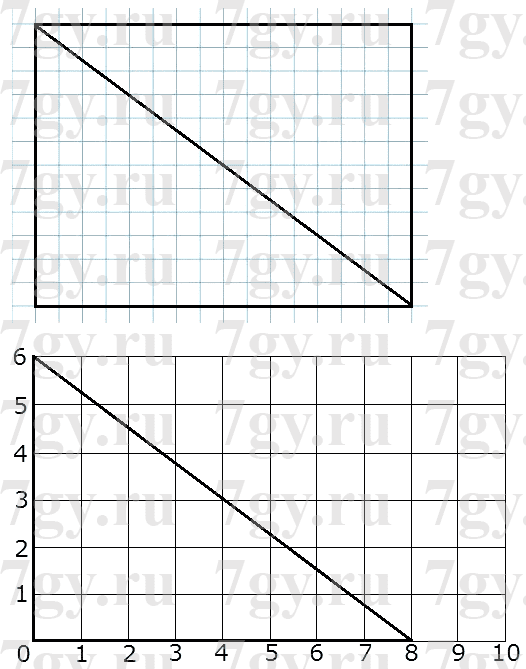
364. Начерти прямоугольник с длиной сторон 8 см и 6 см. Построй диагональ в этом прямоугольнике. Измерь длину этой диагонали.
На какие два треугольника разбит построенный прямоугольник? Вычисли периметр любого из треугольников.
Вычисли площадь прямоугольника и площадь одного прямоугольного треугольника.
Измерь площадь этого треугольника с помощью палетки, заменяя каждые два неполных квадрата на один полный квдрат. Сравни результат, полученный вычислением, с результатом измерения с помощью палетки.

Диагональ 10 см.
На два одинаковых прямоугольных треугольника.
Периметр треугольника: 6 + 8 + 10 = (24 см).
Площадь прямоугольника: 6 • 8 = 48 (кв. см).
Площадь треугольника: 48 : 2 = 24 (кв. см).
Площадь измерением палеткой 24 кв. см.

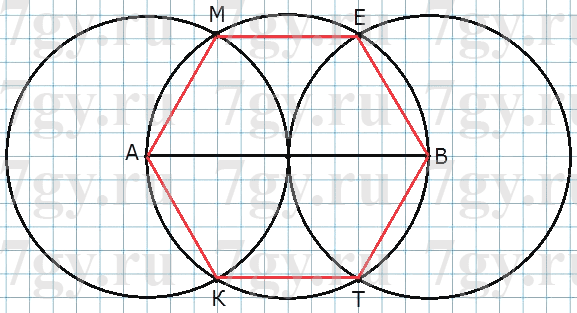
365. Начерти окружность радиусом 3 см. Проведи диаметр этой окружности и обозначь концы диаметра буквами А и В. Начерти ещё две окружности того же радиуса, что и первая окружность, но с центрами соответственно в точках А и В. Отметь точки пересечения этих окружностей с первой окружностью и обозначь эти точки буквами М, Е, К и Т. Охарактеризуй многоугольник, вершины которого находятся в шести обозначенных буквами точках.

Полученный шестиугольник имеет равные стороны, так как каждая сторона — это радиус окружности.

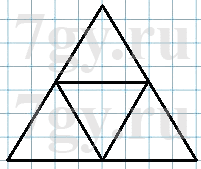
366. Построй равносторонний треугольник с длиной стороны 4 см. Разбей его на 4 одинаковых равносторонних треугольника.

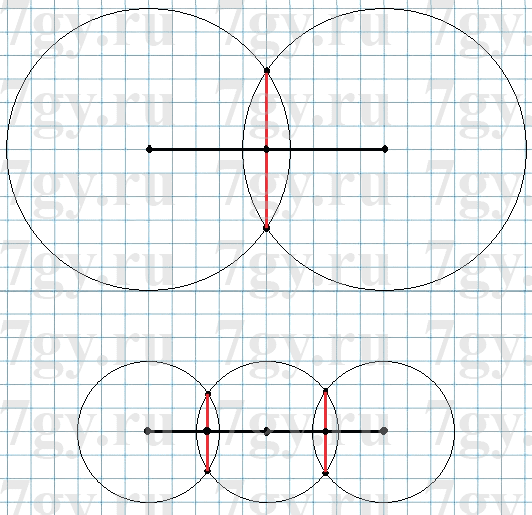
367. Начерти отрезок длиной 5 см. С помощью циркуля и линейки раздели его на 4 равные части.

Начертим две окружности из каждого конца отрезка радиусом чуть больше половины длины отрезка («на глаз»). Точки пересечния этих окружностей между собой соединим отрезком. Этот отрезок проходит перпендикулярно исходному отрезку, точка их пересечения и будет серединой исходного отрезка. Аналогично поступаем для двух половин исходного отрезка и делим их на две равные части — в итоге получаем четыре равных отрезка.