Страница 44

Урок 17 Свойства объединения множеств

1. Сравни равенства в каждом столбце, каждой строке. Что в них общего? Какие свойства они выражают?

а + b = b + a
a • b = b • a
A ∩ B = B ∩ A
(а + b) + c = a + (b + c)
(a • b) • c = a • (b • c)
(A ∩ B) ∩ C = A ∩ (B ∩ C)

Все ли операции над числами обладают этими свойствами?

2. А = {к; м; п}, В = {а; м; к; р}. Запиши с помощью фигурных скобок множества А ∪ В и В ∪ А. Покажи их на диаграмме Эйлера–Венна. Что ты замечаешь?

А ∪ В = {к; м; п; а; р}

В ∪ А = {к; м}

Сделай вывод.

При объединении множеств в результате фигурируют все элементы этих множеств, а при пересечении лишь общие элементы, встречающиеся в одном и другом множестве.

3. Нарисуй диаграмму множеств А, В и С. Раскрась на ней сначала множество А ∪ В, потом множество С, а затем обведи их объединение (А ∪ В) ∪ C. Аналогично построй диаграмму множества А ∪ (В ∪ C).

(А ∪ В) ∪ C =
А ∪ (В ∪ C) =

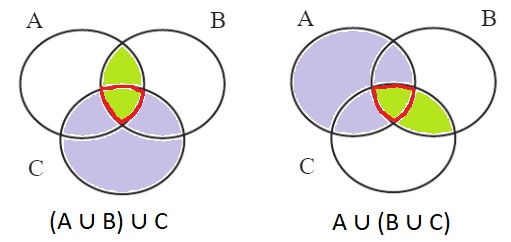
Сравни полученные множества. Что ты замечаешь? Сделай вывод.

Свойства объединения множеств

Объединение множеств обладает переместительным и сочетательным свойствами.
Переместительное свойство: А ∪ В = В ∪ А
Сочетательное свойство: (А ∪ В) ∪ C = А ∪ (В ∪ C)
Значит, результат объединения множеств не зависит от порядка множеств и от порядка действий.

4. Допиши в тетради равенства, выражающие свойства объединения множеств. Назови эти свойства и объясни их смысл.

М ∪ К =K ∪ M

(М ∪ К) ∪ Т = М ∪ (К ∪ Т)