Страница 31
Урок 11
Свойства пересечения множеств
1.
а) Назови записанные свойства сложения и умножения. В чём их смысл?
а + b = b + a
а • b = b • a
(а + b) + c = a + (b + c)
(а • b) • c = a • (b • c)
В том, что при выполнении вычислений этих выражений не важен порядок действий и возможно использовать перестановки.
б) Обладают ли этими свойствами вычитание и деление? Обоснуй свой ответ.
Нет, не обладает. Для этого лучше всего привести пример.
9 : 3 ≠ 3 : 9
9 - 3 ≠ 3 - 9
2. А = {1; 2; 3; 4}, В = {3; 4; 5}. Запиши с помощью фигурных скобок множества А ∩ В и В ∩ А. Покажи их на диаграмме Эйлера–Венна. Что ты замечаешь?
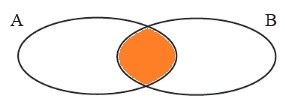
А ∩ В = {3; 4} B ∩ A = {3; 4}
Сделай вывод.
Пересечение элементов двух множеств одно и тоже, не важно берем ли мы пересечение первого множества во втором или второго в первом.
3. Нарисуй диаграмму множеств А, В и С. Закрась на ней сначала А ∩ В, потом С, а затем обведи их пересечение (А ∩ В) ∩ C. Аналогично построй диаграмму множества А ∩ (В ∩ C).
(А ∩ В) ∩ C =
А ∩ (В ∩ C) =
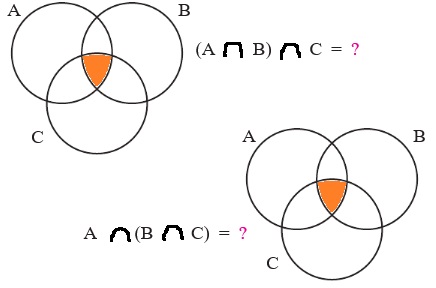
Сравни полученные множества. Что ты замечаешь? Сделай вывод
Свойства пересечения множеств
Пересечение множеств обладает переместительным и сочетательным свойствами.
Переместительное свойство: А ∩ В = В ∩ А
Сочетательное свойство: (А ∩ В) ∩ C = А ∩ (В ∩ C)
Значит, результат пересечения множеств не зависит от порядка множеств и от порядка действий.
4. Допиши в тетради равенства, выражающие свойства пересечения множеств. Назови эти свойства и объясни их смысл.
М ∩ К = К ∩ М (М ∩ К) ∩ Т = Т ∩ (М ∩ К)

