Ответы к странице 129
Задание 688
Найдите квадраты чисел 2; 5; 7; 8; 10; 20. Найдите кубы чисел 2; 3; 5; 10; 30.
Решение
22 = 2 * 2 = 4 ,
52 = 5 * 5 = 25 ,
72 = 7 * 7 = 49 ,
82 = 8 * 8 = 64 ,
102 = 10 * 10 = 100 ,
202 = 20 * 20 = 400 ,
23 = 2 * 2 * 2 = 8 ,
33 = 3 * 3 * 3 = 27 ,
53 = 5 * 5 * 5 = 25 * 5 = 125 ,
103 = 10 * 10 * 10 = 100 * 10 = 1000 ,
303 = 30 * 30 * 30 = 900 * 30 = 27000 .
Задание 689
Квадрат какого числа равен 4; 16; 36; 81; 900? Куб какого числа равен 1; 8; 64; 125; 27000?
Решение
22 = 4 ,
42 = 16 ,
62 = 36 ,
92 = 81 ,
302 = 900 ,
13 = 1 ,
23 = 8 ,
43 = 64 ,
53 = 125 ,
303 = 27000 .
Задание 690
Вычислите наиболее простым способом:
а) 4 * 19 * 25;
6) 8 * 15 * 125;
в) 250 * 35 * 8;
г) 50 * 75 * 2;
д) 16 * 47 * 125;
е) 40 * 8 * 25 * 125.
Решение 7 гуру
а) 4 * 19 * 25 = (4 * 25) * 19 = 100 * 19 = 1900
б) 8 * 15 * 125 = 15 * (125 * 8) = 15 * 1000 = 15000
в) 250 * 35 * 8 = (250 * 4) * (2 * 35) = 1000 * 70 = 70000
г) 50 * 75 * 2 = (50 * 2) * 75 = 100 * 75 = 7500
д) 16 * 47 * 125 = (2 * 47) * (8 * 125) = 94 * 1000 = 94000
e) 40 * 8 * 25 * 125 = (125 * 8) * (40 * 25) = 1000 * 1000 = 1000000
Задание 691
Изменится ли частное двух чисел, если:
а) делимое увеличить в 2 раза; в 3 раза;
б) делимое и делитель увеличить в одинаковое число раз?
Приведите примеры.
Решение
а) При увеличении делимого в n раз частное также увеличится в n раз:
15 : 5 = 3; 30 : 5 = 6.
б) При увеличении делимого и делителя в одинаковое число раз частное не изменится:
15 : 5 = 3; 30 : 10 = 3.
Задание 692
Расскажите, в каком порядке надо выполнять действия при нахождении значения выражения:
а) 23 * 82 ? 15 * 33 + 1734 : 17;
б) 5 * 113 ? 4 * (76 + 132 ? 5).
Решение
a) 23 * 82 ? 15 * 33 + 1734 : 17 = 23 * 64 ? 15 * 27 + 1734 : 17 = 1472 ? 405 + 102 = 1169
б) 5 ? 113 + 4 * (76 + 132 ? 5) = 5 ? 1331 + 4 ? (76 + 169 ? 5) = 5 ? 1331 + 4 * 921 = 3684 + 5 ? 1331 = 2358
Задание 693
Попробуйте найти число, квадрат которого оканчивается цифрой 0; 6; 5; 7.
Какой цифрой может оканчиваться квадрат числа? куб числа?
Решение
102=100,
62=36,
52=25.
Квадрат числа не может оканчиваться цифрами 2, 3, 7, 8.
Куб числа может оканчиваться любой из цифр.
Задание 694
Машина двигалась 4 ч со скоростью а км/ч и 3 ч со скоростью b км/ч. Какой путь прошла машина за эти 7 часов?
Составьте выражение для решения задачи и найдите его значение при: а = 40, b = 30; а = 30, b = 40; а = 60, b = 70.
Решение
Машина за 7 ч прошла путь (4а + 3b) км.
При а = 40, b = 30
4а + 3b = 4 * 40 + 3 * 30 = 160 + 90 = 250
Ответ: 250 км.
При а = 30, b = 40
4а + 3b = 4 * 30 + 3 * 40 = 120 + 120 = 240
Ответ: 240 км.
При а = 60 = 70
4а + 3b = 4 * 60 + 3 * 70 = 240 + 210 = 450
Ответ: 450 км.
Задание 695
Найдите значение выражения:
а) 32 + 42 ;
б) ( 42 + 1 )2 ;
в) ( 92 ? 42 ) : ( 9 ? 4 ) ;
г) ( 83 + 73 ) : ( 82 ? 72 ) .
Решение
а) 32 + 42 = 9 + 16 = 25
б ) ( 42 + 1 )2 = ( 16 + 1 ) 2 = 172 = 289
в ) ( 92 ? 42 ) : ( 9 ? 4 ) = ( 81 ? 16 ) : 5 = 65 : 5 = 13
г ) ( 83 + 73 ) : ( 82 ? 72 ) = ( 512 + 343 ) : ( 64 ? 49 ) = 855 : 15 = 57
Задание 696
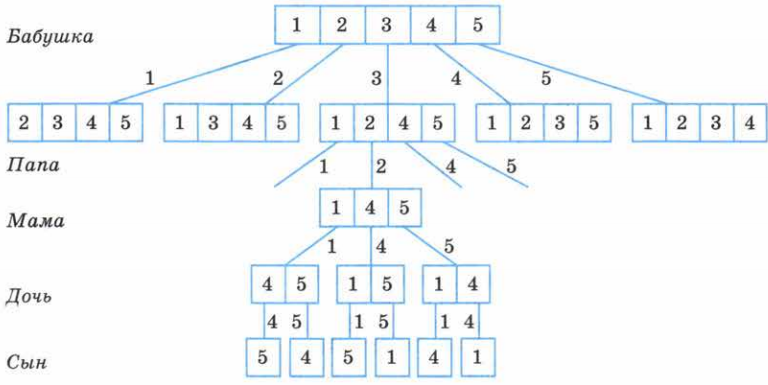
Семье, состоящей из бабушки, папы, мамы, дочери и сына, подарили 5 разных чашек. Сколькими способами можно разделить чашки между членами семьи?
Решение
У первого члена семьи (например, бабушки) есть 5 вариантов выбора, у следующего (пусть это будет папа) остаётся 4 варианта выбора, следующий (например, мама) будет выбирать уже из 3 чашек, следующий ? из двух, последний же получает одну оставшуюся чашку. Покажем эти способы на схеме.
Получили, что каждому выбору чашки бабушкой соответствует четыре возможных выбора папы, т. е. всего 5 * 4 способов. После того как папа выбрал чашку, у мамы есть три варианта выбора, у дочери ? два, у сына ? один, т. е. всего 3 * 2 * 1 способов.
Окончательно получаем, что для решения задачи надо найти произведение 5 * 4 * 3 * 2 * 1.
Заметим, что получили произведение всех натуральных чисел от 1 до 5. Такие произведения записывают короче:
5 * 4 * 3 * 2 * 1 = 5! (читают: «пять факториал»).
Итак, ответ задачи: 5! = 120, т. е. чашки между членами семьи можно распределить ста двадцатью способами.