Страница 31

1. Мальчик рассаживал солдатиков в машинки. Если он сажал в каждую машинку по 2 солдатика, то 4 солдатика оставались без машинки. Если он сажал в каждую машинку по 3 солдатика, то в одной машинке оказалось только 2 солдатика. Сколько машинок и сколько солдатиков было у мальчика?

Данную задачу можно решить методом подбора или составлением уравнения.

Решение методом подбора:
Используем условие, что если в каждую машинку сажать по 3 солдатика, то в одной машинке оказывается только 2 солдатика. То есть машинок уже не меньше двух. Подбирая количество машинок также проверяем полученный ответ по условию, что если в каждой машинке по 2 солдатика, то 4 солдатика остаётся без машинки.
2 машинки: 3 + 2 = 5 (солдатиков), 5 - 4 = 1 (солдатик) в машинку - не подходит.
3 машинки: 3 + 3 + 2 = 8 (солдатиков), 8 - 4 = 4 (солдатика) в машинки: 4 : 2 = 2 (машинки) - не подходит, у нас 3 машинки.
4 машинки: 3 + 3 + 3 + 2 = 11 (солдатиков), 11 - 4 = 7 (солдатиков) в машинки: 7 : 2 - не подходит.
5 машинок: 3 + 3 + 3 + 3 + 2 = 14 (солдатиков), 14 - 4 = 10 (солдатиков) в машинки: 10 : 2 = 5 (машинок) - оба условия задачи выполнены.

Решение через уравнение:
Обозначим количество машинок через х. Тогда, из первого условия задачи, количество солдатиков будет: 2 • х + 4 (4 солдатика остались без машинки и мы их прибавляем к произведению солдатиков и машинок). А из второго условия то же количество солдатиков будет: 3 • х - 1 (в одной машинке оказалось на одного солдатика меньше - его мы и вычитаем из произведения солдатиков и машинок). Получаем: 2 • х + 4 = 3 • х - 1. Группируем известные и неизвестные величины: 4 + 1 = 3 • х - 2 • х. Получаем: 5 = х. То есть, машинок 5 штук. Тогда солдатиков будет: 2 • 5 + 4 = 14 (штук) или 3 • 5 - 1 = 14 (штук).
Ответ: у мальчика было 5 машинок и 14 солдатиков.

2. Выбери все высказывания, верные для этого рисунка:

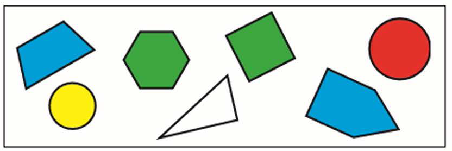
3) Если фигура не закрашена, то это прямой треугольник.
Закончи высказывания, верные для данного рисунка:

Если фигура шестиугольник, то она зелёного цвета.
Если фигура зелёного цвета, то это равносторонний многоугольник.

3. Вычислительная машина работает так:

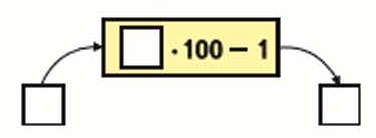
1) Какое число будет получаться на выходе из машины, если в неё ввели число: 2 → 199, 200 → 19 999, 100 → 9 999, 50 → 4 999, 300 → 29 999.
2) Какое число ввели в машину, если на выходе получили число: 2 ← 199, 60 ← 5 999, 4 ← 399.