Страница 87

7. 
75 + x = 90
x = 90 − 75
x = 15

80 − k = 42
k = 80 − 42
k = 38

6 * n = 54
n = 54 : 6
n = 9

8. 
1) Найди площадь прямоугольника BCKE и площадь прямоугольника AEKD.
2) Найди двумя способами площадь прямоугольника ABCD.

Решение 1
BC = EK = AD = CK = BE = 2 см;
KD = EA = 3 см;
SBCKE=BC∗CK=2∗2=4 (см2);
SAEKD=EK∗KD=2∗3=6(см2).

Решение 2
Способ 1.
AB = CD = 5 см;
BC = AD = 2 см;
SABCD=AB∗AD=5∗2=10(см2).

Способ 2.
BC = EK = AD = CK = BE = 2 см;
KD = EA = 3 см;
SBCKE=BC∗CK=2∗2=4 (см2);
SAEKD=EK∗KD=2∗3=6 (см2);
SABCD=SBCKE+SAEKD=4+6=10(см2).

9. 
1) Сделай такой же чертеж в тетради и подумай, как можно узнать площадь каждой из фигур с общей стороной OK (рис. 1); с общей стороной NP
2) Узнай, площадь какой фигуры меньше: прямоугольника BCKE или треугольника OKD − и на сколько квадратных сантиметров.

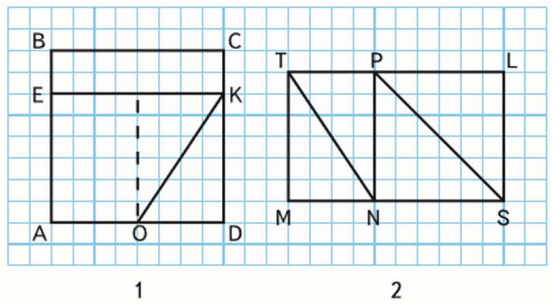
Решение 1
Фигуры с общей стороной OK: OKD, OKCBA и OAEK;
SOKD=SOFKD:2=(DK∗OD):2=(3∗2):2=6:2=3(см2);
SOKCBA=SBCKE+SOFK+SEFOA=SBCKE+SOFKD:2+SEFOA=BC∗CK+(DK∗OD):2+AO∗AE=4∗1+(3∗2):2+2∗3=4+6:2+6=4+3+6=7+6=13(см2);
SOAEK=SOFK+SEFOA=(DK∗OD):2+AO∗AE=(3∗2):2+2∗3=6:2+6=3+6=9(см2).
Фигуры с общей стороной NP: TMNP, NPLS, NPS и NPT;
STMNP=NP∗TP=3∗2=6 (см2);
SNPLS=NP∗PL=3∗3=9 (см2);
SNPS=SNPLS:2=(NP∗PL):2=(30∗30):2=900:2=450(мм2);
SNPT=STMNP:2=(NP∗TP):2=(3∗2):2=6:2=3(cм2).

Решение 2
SBCKE=BC∗CK=4∗1=4(см2);
SOKD=SOFKD:2=(DK∗OD):2=(3∗2):2=6:2=3(см2);
4 > 3, значит
SBCKE=SOKDна 4 − 3 = 1 (см2).

?. 
На сколько 9 меньше, чем 72?
Во сколько раз 6 меньше, чем 54?

Решение
1) 72 − 9 = на 63 − 9 меньше, чем 72;
2) 54 : 6 = в 9 (раз) − 6 меньше, чем 54.

Задание на полях: 54-6-42-100-25