Страница 63
1. У Сережи 5 монет по 10 к., а у Володи одна монета − 50 к.
1) Поставь вопрос, чтобы задача решалась так:
10 * 5 + 50.
2) Поставь к тому же условию другой вопрос, чтобы задача решалась так:
10 * 5 − 50.
Вопрос 1:
Сколько всего денег у мальчиков?
Решение:
10 * 5 + 50 = 50 + 50 = 100 (к.) = 1 (р.) − всего денег у мальчиков.
Ответ: у мальчиков всего 1 р.
Вопрос2:
У кого из мальчиков денег больше и на сколько?
Решение:
10 * 5 − 50 = 50 − 50 = 0 (к.) − разница количества денег у ребят, то есть у ребят одинаковое количество денег.
Ответ: у мальчиков одинаковое количество денег.
2.
9 * 4 = 36;
7 * 8 = 56;
8 * 9 = 72;
56 : 8 * 5 = 7 * 5 = 35;
64 : 8 * 7 = 8 * 7 = 56;
42 : 7 * 8 = 6 * 8 = 48;
91 − (6 + 85) = 91 − 91 = 0;
55 + 8 − 29 = 63 − 29 = 34;
41 − 5 + 36 = 36 + 36 = 72;
6 * 3 = 18;
1 * 3 = 3;
0 * 3 = 0.
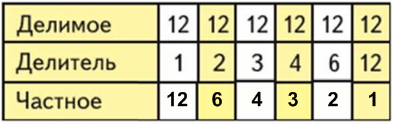
3. 
4. Сравни задачи, сравни их решения.
1) 8 одинаковых наборов цветной бумаги стоят 80 р. Сколько стоят 5 таких наборов?
2) 8 одинаковых наборов цветной бумаги стоят 80 р. Сколько таких наборов бумаги можно купить на 60 р.?
Решение
Задача 1.
1) 80 : 8 = 10 (р.) − цена одного набора;
2) 10 * 5 = 50 (р.) − стоимость 5 наборов.
Ответ: 5 наборов цветной бумаги стоят 50 р.
Задача 2.
1) 80 : 8 = 10 (р.) − цена одного набора;
2) 60 : 10 = 6 (наборов) − можно купить 6 наборов.
Ответ: на 60 р. можно купить 6 наборов.
В обеих задачах нам известна общая стоимость определенного количества наборов. Поэтому первым действием в обоих случаях мы сначала делим стоимость на количество и, таким образом, находим цену за штуку.
В первой задаче нам нужно найти стоимость какого−то количества, поэтому мы цену умножаем на это количество. А во второй задаче нам нужно найти количество, зная общую стоимость, поэтому мы делим стоимость на цену и находим количество.
5.
26 − 6 − 7 = 20 − 7 = 13;
7 + 9 + 2 = 16 + 2 = 18;
9 + 9 + 2 = 18 + 2 = 20;
9 * 2 − 2 = 18 − 2 = 16;
2 * 2 − 4 = 4 − 4 = 0;
8 * 9 − 2 = 72 − 2 = 70;
8 * 4 − 2 = 32 − 2 = 30;
40 : 5 * 7 = 8 * 7 = 56.
6.
x + 34 = 68;
x + 38 = 68.
В обоих уравнениях, чтобы найти x, нужно из суммы вычесть известное слагаемое. Так как суммы одинаковые, то значение x будет больше в том уравнении, где второе слагаемое меньше, то есть в уравнении x + 34 = 68.
96 − x = 15;
96 − x = 18.
В обоих уравнениях, чтобы найти x, нужно из уменьшаемого вычесть разность. Так как в уравнениях уменьшаемые равны, то значение x будет больше в том уравнении, в котором разность меньше, то есть в уравнении 96 − x = 15.
x − 29 = 60;
x − 39 = 60.
В обоих уравнениях, чтобы найти x, нужно к разности прибавить вычитаемое. Так как в уравнениях разность одинакова, то значение x будет больше в том уравнении, где вычитаемое больше, то есть в уравнении x − 39 = 60.
?.
24 : 8 = 3;
56 : 7 = 8;
6 * 8 = 48;
8 * 4 = 32.
На полях: 19-36-24-6-30

