Страница 93:

1. Какие остатки могут получиться при делении на 3, на 5, на 12, на x?

на 3 (0 - без остатка, 1, 2)
на 5 (0 - без остатка, 1, 2, 3, 4)
на 12 (0 - без остатка, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11)

2. Найди по рисунку делимое, делитель, частное и остаток. Запиши в тетради соответствующее числовое равенство.

20 = 6 * 3 + 2

3.

а) Проверь равенства, выражающие связь между компонентами деления с остатком:

11 = 4 • 2 + 3

17 = 6 • 2 + 5

19 = 5 • 3 + 4

Сделай чертежи. Назови делимое, делитель, частное и остаток. 

Рисунки расположены по порядку, как выражения выше

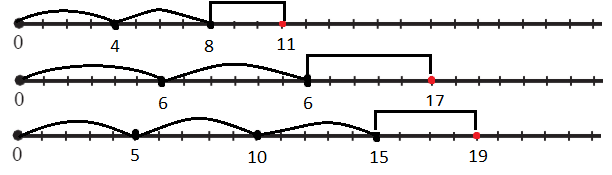
б) Запиши все три равенства одной буквенной формулой, обозначая делимое a, делитель b, частное c и остаток r:

a = b • c + r ,  r < b

Сравни значение остатка r и делителя b. Сделай вывод.

Остаток всегда должен быть меньше делителя.