Ответы к пункту 29. Сложение и вычитание смешанных чисел, страница 51

Задание № 266

В одной коробке 2 3/8 кг конфет, а в другой коробке 2 1/8 кг. Сколько килограммов конфет в этих двух коробках?

Решение

$2\frac38+2\frac18=2+2+\frac38+\frac18=4\frac48$ (кг)
Ответ: $4\frac48$ кг конфет в двух коробках.

Задание № 267

Чему равна длина белой ленты, если длина красной ленты 3 3/5 м, а белая лента на 2 1/5 короче красной?

Решение

$3\frac35-2\frac15=3-2+\frac35-\frac15=1\frac25$ (м)
Ответ:$1\frac25$ м.

Задание № 268 с ответами

Выполните действия:

а) $5+2\frac38=7\frac38$

б) $10\frac34-7=3\frac34$

в) $4\frac16+10=14\frac16$

г) $12\frac8{15}-12=\frac8{15}$

д) $4\frac19+3\frac49=7\frac59$

е) $7\frac57-4\frac37=3\frac27$

ж) $3\frac8{11}+5\frac2{11}=8\frac{10}{11}$

з) $9\frac7{12}-7\frac6{12}=2\frac1{12}$

и) $4\frac35+2\frac45=6\frac75=7\frac25$

к) $8\frac9{13}+7\frac{12}{13}=15\frac{21}{13}=16\frac8{13}$

л) $5\frac35-1\frac45=4\frac85-1\frac45=3\frac45$

м) $4\frac5{11}-2\frac8{11}=3\frac{16}{11}-2\frac8{11}=1\frac8{11}$

н) $4-\frac59=3\frac99-\frac59=3\frac49$

о) $8-\frac7{12}=7\frac{12}{12}-\frac7{12}=7\frac5{12}$

п) $5-3\frac38=4\frac88-3\frac38=\frac58$

р) $4-3\frac59=3\frac99-3\frac59=\frac49$

Задание № 269

Найдите значение выражения:

а) $4\frac7{12}-1\frac5{12}+2\frac{11}{12}=(4-1+2)+(\frac7{12}-\frac5{12}+\frac{11}{12})=5+\frac{13}{12}=5\frac{13}{12}=6\frac1{12}$

б) $6\frac{14}{15}-3\frac2{15}-1\frac7{15}=(6-3-1)+(\frac{14}{15}-\frac2{15}-\frac7{15})=2+\frac5{15}=2\frac5{15}$с

Задание № 270

На базу привезли яблоки на двух грузовиках. На первом было 4 3/10
т яблок, а на втором − на 1 1/10 т меньше. Сколько тонн яблок привезли на базу? Выразите ответы в центнерах.

Решение

$4\frac3{10}+(4\frac3{10}-1\frac1{10})=\frac{43}{10}+3\frac2{10}=7\frac5{10}$ (т)
10 : 10 * 75 = 75 (ц)
Ответ: $7\frac5{10}$ т, 75 ц.

Задание № 271

Два шахматиста сыграли две партии: первая партия продолжалась 1 1/4 ч, а вторая − на 3/4 ч больше. Сколько часов продолжалась игра? Выразите продолжительность игры в минутах.

Решение

1) $1\frac14+\frac34=1\frac44=2$ (ч) - продолжалась вторая партия
2) $1\frac14+2=3\frac14$ (ч) - продолжалась игра
3) 60 * 3 + 60 : 4 = 180 + 15 = 195 (мин) - продолжалась игра
Ответ: $3\frac14$ч, 195 мин.

Задание № 272

Вычислите устно:
а) 8² : 4
+56
:18
*25
−61
?
б) 3³ * 2
:6
*7
+7
+230
?
в) 10² * 3
:150
*48
+44
:7
?
г) 4³ : 8
*9
+19
:13
*120
?
д) 5² * 8
:40
*60
−120
:30
?

Ответы

a) 64, 16, 72, 4, 100, 39.
б) 27, 54, 9, 63, 70, 300.
в) 100, 300, 2, 96, 140, 20.
г) 64, 8, 72, 91, 7, 840.
д) 25, 200, 5, 300, 180, 6.

 

Задание № 273

Восстановите цепочку вычислений: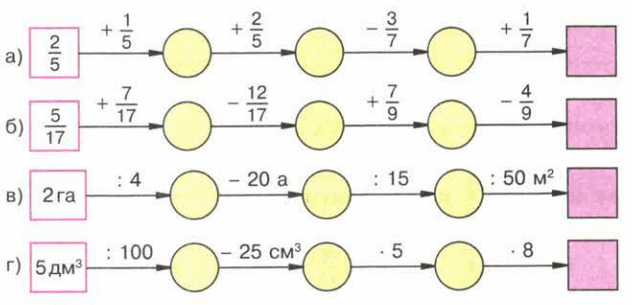

Решение

Задание № 274

Каковы координаты точек, отмеченных на рисунке 136? Чему равно расстояние (в единичных отрезках) между точками:
О и Е, О и К, О и С, D и С, А и Е, М и Е? Сравните координаты точек С и D, С и Е, М и К, N и А, А и В.

Решение

$0(0),D(\frac25),{\operatorname С}(\frac35),E(1),{\operatorname А}(\frac85),K(2),{\operatorname М}(\frac{13}5),N(\frac{14}5),B(\frac{16}5)$
$OE=1,OK=2,OC=\frac35,DC=\frac15,AE=\frac35,ME=\frac85$
$\frac25<\frac35;\frac35<1;2<\frac{13}5;\frac85<\frac{14}5;\frac85<\frac{16}5$

Задание № 275

Между какими натуральными числами на координатном луче расположены смешанные числа: 1 5/7, 3 1/10, 15 2/9, 1200 1/100?

Решение

$1<1\frac57<2$
$3<3\frac1{10}<4$
$15<15\frac29<16$
$1200<1200\frac1{100}<1201$

Задание № 276

При каких значениях а частное 12 : а будет:
а) натуральным числом;
б) неправильной дробью;
в) правильной дробью?
Ответьте на те же вопросы для частного а : 6.

Ответы

а) 12 : a: при а равном 1; 2; 3; 4; 6; 12;
a : 6: при а кратным 6.
б)12 : a: при а равном 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12;
a : 6: при а > 6.
в) 12 : a: при натуральном а > 12;
a : 6: при a < 6 частное.

Задание № 277

Составьте задачу по уравнению:
а) $x+\frac29=\frac79$
б) $y-\frac57=\frac17$
в) $3\frac58-z=2$

Решение

а) Тракторист за день вспахал 7/9 поля, причем после обеда он вспахал 2/9 поля. Какую часть поля вспахал тракторист до обеда.
Пусть до обеда тракторист вспахал х поля
$x+\frac29=\frac79$
$x=\frac79-\frac29$
$x=\frac59$
Ответ: $\frac59$ поля вспахал тракторист до обеда.

б) За день семья выкопала 5/7 огорода картофеля и им осталось выкопать еще 1/7 часть. Какая часть огорода была не выкопанной на начало дня?
Решение:
Пусть на начало дня было не выкопано y огорода, тогда:
$y-\frac57=\frac17$
$y=\frac17+\frac57$
$y=\frac67$
Ответ: $\frac67$ огорода было не выкопано.

в) В магазине было 3 5/8 мешка сахара. Сколько мешков сахара было продано, если на конец дня осталось два мешка.
Пусть продали z мешков, тогда:
$3\frac58-z=2$
$z=3\frac58-2$
$z=1\frac58$
Ответ: $1\frac58$ мешка сахара было продано.

 

Задание № 278

По рисунку 137 составьте уравнение и решите его.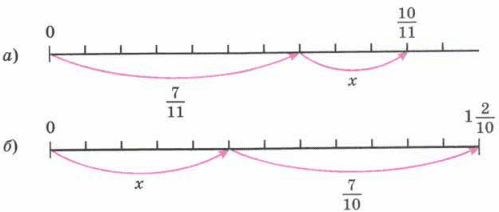

Решение

а) $\frac7{11}+{\operatorname х}=\frac{10}{11}$
$x=\frac{10}{11}-\frac7{11}$
$x=\frac3{11}$

б) $x+\frac7{10}=1\frac2{10}$
$x=1\frac2{10}-\frac7{10}$
$x=\frac{12}{10}-\frac7{10}$
$x=\frac5{10}$

Задание № 279

В старинных книгах можно встретить такие названия дробей: 1/2 − пол, полтина; 1/5 − пятина; 1/7 − седьмина; 1/10 − десятина.
Подумайте, как появились следующие названия: 1/4 − четь; 1/8 − полчети; 1/16 − полполчёти; 1/32 − полполполчети (малая четь).
Дробь 1/3 называли «треть».
Попробуйте догадаться, как называли дроби: 1/6, 1/12, 1/24.
Подумайте, почему смешанные числа называли:
1 1/2 − полвтора; 2 1/2 − полтретья; 3 1/2 − полчётверта; 4 1/2 − полпяты; 5 1/2 − полшесты и т. д.
Сохранился ли такой способ чтения в наше время?

Решение

В наше время такой способ чтения не сохранился.

Задание № 280

Из дробей 49/5; 11/3; 19/12; 48/16; 355/100; 817/121; 3407/1000 выделите целую часть, а смешанные числа 1 2/3; 5 4/11; 7 13/17; 9 45/51; 8 9/1000; 6 13/1000 запишите в виде неправильных дробей.

Решение

Задание № 281

Выполните действия:

а) $\frac6{19}-\frac3{19}+\frac{15}{19}=\frac{6-3+15}{19}=\frac{18}{19}$
б) $\frac{19}{21}-\frac{17}{21}+\frac9{21}=\frac{19-17+9}{21}=\frac{11}{21}$
в) $\frac{25}{32}-\frac6{32}+\frac{19}{32}=\frac{25-6+19}{32}=\frac{38}{32}=1\frac6{32}$

Задание № 282

Лесник прошёл 3 км и 4 ч ехал на лошади. С какой скоростью он ехал на лошади, если весь путь равен 34 км?

Решение

1) 34 − 3 = 31 (км) - проехал лесник на лошади
2) $31:4=\frac{31}4=7\frac34$ (км/ч) - скорость, с которой он ехал на лошади
Ответ: $7\frac34$ км/ч.

Задание № 283

Пошёл дождь. Под водосточную трубу поставили пустую бочку. В неё вливалось каждую минуту 8 л воды, а через щель в бочке выливалось 3 л воды в минуту.
Сколько литров воды будет в бочке через 1 мин; 2 мин; 3 мин?
Успеет ли бочка наполниться, если её объём 400 л, а дождь шёл 1 ч 10 мин?

Решение

Через t мин в бочке будет (8 − 3)t = 5t (л) воды
Через 1 мин в бочке будет 5 * 1 = 5 (л)
через 2 мин: 5 * 2 = 10 (л)
через 3 мин: 5 * 3 = 15 (л)
За 1 ч 10 мин = 70 мин в бочке будет 5 * 70 = 350 л, что меньше 400 л, значит бочка не успеет наполниться водой.
Ответ: 5 л, 10 л, 15 л. Не успеет.

Задание № 284

Легковой автомобиль движется со скоростью 70 км/ч, а грузовой − со скоростью 40 км/ч. Сейчас легковой автомобиль находится сзади грузовика на расстоянии 60 км. Оба автомобиля движутся в одном направлении. Какое расстояние будет между ними через 1 ч, через 2 ч, через 3 ч?

Решение

Через t ч между автомобилями будет расстояние
60 − (70 − 40)t = 60 − 30t (км)
через 1 ч: 60 − 30 * 1 = 30 (км)
через 2 ч: 60 − 30 * 2 = 60 − 60 = 0 (км) легковой автомобиль догонит грузовой
через 3 ч: 30 * 3 − 60 = 90 − 60 = 30 (км) легковой автомобиль обгонит грузовой
Ответ: 30 км, 0 км, 30 км.

Задание № 285

Решите задачу:
1) В третьем классе 35 учеников. Из них 5/7 умеют играть в шахматы. Сколько ребят в этом классе ещё не научились играть в шахматы?
2) В бригаде 15 человек. Из них 2/5 владеют только одной специальностью, а остальные − двумя. Сколько человек в бригаде владеют двумя специальностями?

Решение

1) 1) 35 : 7 * 5 = 25 (р.) - умеют играть в шахматы
2) 35 − 25 = 10 (р.) - не умеют играть в шахматы
Ответ: 10 ребят.

2) 1) 15 : 5 * 2 = 6 (ч.) - владеют одной специальностью
2) 15 − 6 = 9 (ч.) - владеют двумя специальностями
Ответ: 9 человек.

Задание № 286

Найдите значение выражения:
1) (38 * 35 − 35) : 259;
2) (43 * 21 + 1671) : 429.

Решение

1) (38 * 35 − 35) : 259 = (1330 − 35) : 259 = 1295 : 259 = 5
2) (43 * 21 + 1671) : 429 = (903 + 1671) : 429 = 2574 : 429 = 6

Задание № 287 с ответами

Выполните действия:

а) $3+8\frac5{12}=11\frac5{12}$

б) $10\frac67-3=7\frac67$

в) $4\frac2{13}+5\frac7{13}=9\frac9{13}$

г) $8\frac7{12}-4\frac2{12}=4\frac5{12}$

д) $4\frac8{11}+5\frac7{11}=9\frac{15}{11}=10\frac4{11}$

е) $7\frac59-2\frac89=6\frac{14}9-2\frac89=4\frac69$

ж) $7-\frac38=6\frac88-\frac38=6\frac58$

з) $10-3\frac7{15}=9\frac{15}{15}-3\frac7{15}=6\frac8{15}$

Задание № 288

Длина прямоугольника 1 4/20 м, а ширина на 3/20 м меньше длины. Найдите периметр прямоугольника.

Решение

1) $1\frac4{20}-\frac3{20}=1\frac1{20}$ (м) - ширина прямоугольника
2) $1\frac4{20}+1\frac4{20}+1\frac1{20}+1\frac1{20}=4\frac{10}{20}$ (м) - периметр
Ответ: $4\frac{10}{20}$ м.

Задание № 289

В один из дней зимних каникул мальчик 2 3/5 ч катался на лыжах, а на коньках на 1 4/5 ч меньше. Сколько всего времени он катался на лыжах и коньках?

Решение

1) $2\frac35-1\frac45=1\frac85-1\frac45=\frac45$ (ч) мальчик катался на коньках
2) $2\frac35+\frac45=2\frac75=3\frac25$ (ч) мальчик катался на лыжах и коньках
Ответ: $3\frac25$ ч.

Задание № 290

Верёвку длиной 256 м разрезали на две части, одна из которых в 7 раз длиннее второй. На сколько метров одна часть верёвки длиннее второй?

Решение

Пусть х − длина короткой части, тогда длина длинной части 7х.
x + 7x (м) - длина веревки
256 (м) - длина веревки
Составляем уравнение:
x + 7x = 256
1x + 7x = 256
(1+7) x = 256
8 x = 256
x = 256 : 8
х = 32 (м) - длина короткой части
32*7=224(м) - длина длинной части
224 - 32 = 192 (м)
Ответ: одна часть на 192 м длиннее второй.

Задание № 291

В археологических раскопках древнего города участвовали две экспедиции. В первой было в три раза больше сотрудников, чем во второй. Когда во вторую экспедицию прибыли ещё 18 человек, то в двух экспедициях вместе стало 66 сотрудников. Сколько стало сотрудников во второй экспедиции?

Решение

Пусть во второй экспедиции было х человек, тогда 3х человек было в первой экспедиции.
Всего в обеих экспедициях было (3х + х) человек.
Составим уравнение:
3х + (х + 18) = 66
4х = 66 − 18 = 48
х = 48 : 4
х = 12
Значит, 12 сотрудников было во второй экспедиции
12 + 18 = 30 (с.) - стало во второй экспедиции
Ответ: 30 сотрудников.

Задание 292

В куске 112 м материи. Из 11/16 куска сшили детские костюмы. Сколько метров материи осталось?

Решение

1) 112 : 16 * 11 = 7 * 11 = 77 (м) - пошло на костюмы, 
2) 112 − 77 = 35 (м) материи осталось.
Ответ: 35 м.

Задание 293

Площадь прямоугольника 616 м², а его длина 28 м. Найдите площадь такого квадрата, у которого периметр равен периметру прямоугольника.

Решение

b = 616 : 28 = 22 (м) - ширина прямоугольника
Р = 2 * (а + b) = 2 * (28 + 22) = 2 * 50 = 100 (м) - периметр прямоугольника
Так как периметр квадрата также равен 100 м, то
Р : 4 = 100 : 4 = 25 (м) - длина его стороны
S = 25² = 625 (м²) - площадь квадрата
Ответ: 625 м².

Задание 294

Выполните действия:
а) (936 : 24 + 32 * 14) : 487;
б) (43 * 56 + 43 * 44) : 215 − 15.

Решение

а) (936 : 24 + 32 − 14) : 487 = (39 + 448) : 487 = 487 : 487 = 1

б) (43 * 56 + 43 * 44) : 215 − 15 = (2408 + 1892) : 215 − 15 = 4300 : 215 − 15 = 20 − 15 = 5