Пункт 35. Деление десятичных дробей на натуральные числа. Со страницы 95
Задание 491
Выполните деление:
а) 20,7 : 9 = 2,3;
б) 243,2 : 8 = 30,4;
в) 88,298 : 7 = 12,614;
г) 772,8 : 12 = 64,4;
д) 93,15 : 23 = 4,05;
е) 0,644 : 92 = 0,007;
ж) 1 : 80 = 0,0125;
з) 0,909 : 45 = 0,0202;
и) 3 : 32 = 0,09375;
к) 0,01242 : 69 = 0,00018;
л) 1,016 : 8 = 0,127;
м) 7,368 : 24 = 0,307.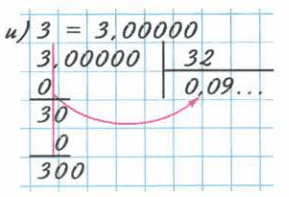
Решение
а)
_20,7 |9
18 |2,3
_27
27
0
б)
_243,2 |8
24 |30,4
_32
32
0
в)
_88,298 |7
7 |12,614
_18
14
_42
42
_9
7
_28
28
0
г)
_772,8 |12
72 |64,4
_52
48
_48
48
0
д)
_93,15 |23
92 |4,05
_115
115
0
е)
_0,644 |92
644 |0,007
0
ж)
_1 |80
0 |0,0125
_10
0
_100
80
_200
160
_400
400
0
з)
_0,909 |45
90 |0,0202
_90
90
0
и)
_3 |32
0 |0,09375
_30
0
_300
288
_120
96
_240
224
_160
160
0
к)
_0,01242 |69
69 |0,00018
_552
552
0
л)
_1,016 |8
8 |0,127
_21
16
_56
56
0
м)
_7,368 |24
72 |0,307
_168
168
0
Задание 492
В самолёт для полярной экспедиции загрузили 3 трактора, массой 1,2 т каждый, и 7 аэросаней. Масса всех аэросаней на 2 т больше массы тракторов. Какова масса одних аэросаней?
Решение
(3 * 1,2 + 2) : 7 = 5,6 : 7 = 0,8 (т) - масса одних аэросаней
Ответ: 0,8 т.
Задание 493
Стороны одного прямоугольника 12 см и 6,6 см. Площадь второго прямоугольника в 11 раз меньше площади первого. Найдите ширину второго прямоугольника, если его длина 8 см.
Решение
12 * 6,6 : 11 : 8 = 79,2 : 11 = 7,2 : 8 = 0,9 (см) - ширина второго прямоугольника
Ответ: 0,9 см.
Задание 494
Турист должен был пройти за два дня 25,2 км. В первый день он прошёл 3 7 пути. Сколько километров прошёл турист во второй день?
Решение
1) 25,2 : 7 * 3 = 3,6 * 3 = 10,8 (км) - прошел турист в первый день
2) 25,2 − 10,8 = 14,4 (км) - прошел турист во второй день
Ответ: 14,4 км.
Задание 495
Собрали 36,9 т клубники. На консервный завод отправили 7/9 собранной клубники, а остальную клубнику передали для продажи населению. Сколько тонн клубники было продано населению?
Решение
1) 36,9 : 9 * 7 = 4,1 * 7 = 28,7 (т) - клубники отправили на консервный завод
2) 36,9 − 28,7 = 8,2 (т) - клубники продали населению
Ответ: 8,2 т.
Задание 496
Для посева было приготовлено 25,2 т семян. В первый день на посев израсходовали 4/9 всех семян, а во второй − 4/7 остатка. Сколько семян осталось после двух дней посева?
Решение
1) 25,2 : 9 * 4 = 2,8 * 4 = 11,2 (т) - семян израсходовали в первый день
2) (25,2 − 11,2) : 7 * 4 = 14 : 7 * 4 = 8 (т) - семян израсходовали во второй день
3) 25,2 − (11,2 + 8) = 25,2 − 19,2 = 6 (т) - семян осталось после двух дней посева
Ответ: 6 т.
Задание 497
На соревнованиях по бегу Вася пробежал дистанцию за 1,2 мин, что составило 5/6 времени, затраченного Колей на эту же дистанцию. За какое время Коля пробежал дистанцию?
Решение
1,2 : 5 * 6 = 0,24 * 6 = 1,44 (мин) - время, за которое Коля пробежал дистанцию
Ответ: за 1,44 мин.
Задание 498
Электрифицировано 16,1 км железной дороги, что составляет 7/9 всей дороги между двумя станциями. Какова длина дороги между этими станциями?
Решение
16,1 : 7 * 9 = 2,3 * 9 = 20,7 (км) - длина дороги между двумя станциями
Ответ: 20,7 км.
Задание 499
Решите уравнение:
а) 4х − х = 8,7;
б) 3y + 5у = 9,6;
в) а + а + 8,154 = 32;
г) 7k − 4k − 55,2 = 63,12.
Решение
а) 4x − x = 8,7
3x = 8,7
x = 8,7 : 3
х = 2,9
б) 3y + 5y = 9,6
8x = 9,6
y = 9,6 : 8
у = 1,2
в) a + a + 8,154 = 32
2a = 32 − 8,154 = 23,846
a = 23,846 : 2
а = 11,923
г) 7k − 4k − 55,2 = 63,12
3k = 63,12 + 55,2 = 118,32
k = 118,32 : 3
k = 39,44
Задание 500
В двух корзинах 16,8 кг помидоров. Масса помидоров в одной корзине в 2 раза больше, чем в другой. Сколько килограммов помидоров в каждой корзине?
Решение
Пусть в одной корзине х кг помидоров, тогда в другой корзине 2х кг.
Составим уравнение:
х + 2х = 16,8
3х = 16,8
х = 16,8 : 3
х = 5,6
Значит, 5,6 кг в одной корзине
2 * 5,6 = 11,2 (кг) - помидоровв другой
Ответ: 5,6 кг, 11,2 кг.
Задание 501
Площадь первого поля в 5 раз больше площади второго. Чему равна площадь каждого поля, если площадь второго на 23,2 га меньше площади первого?
Решение
Пусть у − площадь второго поля, тогда площадь первого поля 5y га.
Составим уравнение:
(5y − у) = 23,2
4у = 23,2
у = 23,2 : 4
у = 5,8
Значит, 5,8 га − площадь второго поля
5 * 5,8 = 29 (га) - площадь первого поля
Ответ: 5,8 га, 29 га.
Задание 502
Для приготовления компота составили смесь из 8 частей (по массе) сухих яблок, 4 частей урюка и 3 частей изюма. Сколько килограммов каждого из сухофруктов понадобилось для 2,7 кг такой смеси?
Решение
Пусть х − масса одной части, тогда:
8x + 4x + 3х = 2,7
x = 2,7 : 15
х = 0,18 (кг)
Следовательно для приготовления 2,7 кг смеси понадобилось:
8 * 0,18 = 1,44 (кг) - яблок
4 * 0,18 = 0,72 (кг) - урюка
3 * 0,18 = 0,54 (кг) - изюма.
Ответ: 1,44 кг, 0,72 кг, 0,54 кг.
Задание 503
В двух мешках 1,28 ц муки. В первом мешке на 0,12 ц муки больше, чем во втором. Сколько центнеров муки в каждом мешке?
Решение
Пусть во втором мешке х ц муки,
тогда в первом мешке (х + 12) ц муки.
Составим уравнение:
х + (х + 0,12) = 1,28
х = (1,28 − 0,12) : 2
х = 0,58
Значит, 0,58 ц во втором мешке
0,58 + 0,12 = 0,7 (ц) - муки в первом мешке
Ответ: 0,58 ц, 0,7 ц.
Задание 504
В двух корзинах 18,6 кг яблок. В первой корзине яблок на 2,4 кг меньше, чем во второй. Сколько килограммов яблок в каждой корзине?
Решение
Пусть в первой корзине х кг яблок, тогда во второй корзине (x + 2,4) кг яблок.
Составим уравнение:
х + (х + 2,4) = 18,6
х = (18,6 − 2,4) : 2
х = 8,1
Значит, 8,1 кг в первой корзине
8,1 + 2,4 = 10,5 (кг) - яблок во второй корзине
Ответ: 8,1 кг, 10,5 кг.
Задание 505
Представьте в виде десятичной дроби:
3/4 ; 5/8 ; 7/4 ; 83/25 ; 5 1/2 ; 70 3/75 ; 4 21/84.
Решение
3/4 = 0,75
5/8 = 0,625
7/4 = 1,75
83/25 = 3,32
5 1/2 = 5,5
70 3/75 = 70,04
4 21/84 = 4,25
Задание 506
Чтобы собрать 100 г мёда, пчела доставляет в улей 16 тыс. нош нектара. Какова масса одной ноши нектара?
Решение
100 : 16000 = 0,00625 (г) - масса одной ноши нектара пчелы
Ответ: 0,00625 г.
Задание 507
В пузырьке 30 г лекарства− Найдите массу одной капли лекарства, если в пузырьке 1500 капель.
Решение
30 : 1500 = 0,02 (г) - масса одной капли лекарства
Ответ: 0,02 г.
Задание 508
Представьте обыкновенную дробь в виде десятичной и выполните действия:
а) 2/3 + 0 , 8;
б) 1,34 − 4/25;
в) 2/3 : 15;
г) 9/60 * (0,6 + 3,4);
д) (2/5 + 0,7) : 11;
е) (7/4 − 0,25) * 27.
Решение
а) 2/3 + 0,8 = 0,75 + 0,8 = 1,55
б) 1,34 − 4/25 = 1,34 − 0,16 = 1,18
в) 2/3 : 15 = 0,6 : 15 = 0,04
г) 9/60 * (0,6 + 3,4) = 0,15 * 4 = 0,6
д) (2/5 + 0,7 ) : 11 = (0,4 + 0,7) : 11 = 1,1 : 11 = 0,1
е) (7/4 − 0,25 ) * 27 = (1,75 − 0,25 ) * 25 = 1,5 * 27 = 40,5
Задание 509
Решите уравнение:
а) (х − 5,46) * 2 = 9;
б) (у + 0,5) : 2 = 1,57.
Решение
а) (x − 5,46) * 2 = 9
x = 9 : 2 + 5,46
х = 9,96
б) (y + 0,5) : 2 = 1,57
у = 1,57 * 2 − 0,5
у = 2,64
Задание 510
Найдите значение выражения:
а) 91,8 : (10,56 − 1,56) + 0,704;
б) (61,5 − 5,16) : 30 + 5,05;
в) 66,24 − 16,24 : (3,7 + 4,3);
г) 28,6 + 11,4 : (6,595 + 3,405);
д) 15,3 − 4 : 9 + 3,2;
е) (4,3 + 2,4 : 8) * 3;
ж) 280,8 : 12 − 0,3 * 24;
з) (17,6 * 13 − 41,6) : 12.
Решение
а) 91,8 : (10,56 − 1,56) + 0,704 = 91,8 : 9 + 0,704 = 10,2 + 0,704 = 10,904
б) (61,5 − 5,16) : 30 + 5,05 = 56,34 : 30 + 5,05 = 1,878 + 5,05 = 6,928
в) 66,24 − 16,24 : (3,7 + 4,3) = 66,24 − 16,24 : 8 = 66,24 − 2,03 = 64,21
г) 28,6 + 11,4 : (6,595 + 3,405) = 28,6 + 11,4 : 10 = 28,6 + 1,14 = 29,74
д) 15,3 − 4 : 9 + 3,2 = 61,2 : 9 + 3,2 = 6,8 + 3,2 = 10
е) (4,3 + 2,4 : 8) * 3 = (4,4 + 0,3) * 3 = 4,7 * 3 = 14,1
ж) 280,8 : 12 − 0,3 * 24 = 23,4 − 7,2 = 16,2
з) (17,6 * 13 − 41,6) : 12 = (228,8 − 41,6) : 12 = 187,2 : 12 = 15,6
Задание 511
Вычислите устно:
а)
2,5 − 1,6;
3,2 − 1,4;
0,47 − 0,27;
0,64 − 0,15;
0,71 − 0,28;
б)
1,8 + 2,5;
2,7 + 1,6;
0,63 + 0,17;
0,38 + 0,29;
0,55 + 0,45;
в)
3,4 − 0,2;
2,6 − 0,05;
4,52 − 1,2;
4 − 0,8;
1 − 0,45;
г)
5 + 0,35;
3,7 + 0,24;
0,46 + 1,8;
0,57 + 3;
1,64 + 0,36.
Решение
а) 2,5 − 1,6 = 0,9
3,2 − 1,4 = 1,8
0,47 − 0,27 = 0,2
0,64 − 0,15 = 0,49
0,71 − 0,28 = 0,43
б) 1,8 + 2,5 = 4,3
2,7 + 1,6 = 4,3
0,63 + 0,17 = 0,8
0,38 + 0,29 = 0,67
0,55 + 0,45 = 1
в) 3,4 − 0,2 = 3,2
2,6 − 0,05 = 2,55
4,52 − 1,2 = 3,32
4 − 0,8 = 3,2
1 − 0,45 = 0,55
г) 5 + 0,35 = 5,35
3,7 + 0,24 = 3,94
0,46 + 1,8 = 2,26
0,57 + 3 = 3,57
1,64 + 0,36 = 2
Задание 512
Выполните умножение:
а) 0,3 * 2;
б) 0,8 * 3;
в) 1,2 * 2;
г) 2,3 * 3;
д) 0,21 * 4;
е) 1,6 * 5;
ж) 3,7 * 10;
з) 0,09 * 6;
и) 0,18 * 5;
к) 0,87 * 0.
Решение
а) 0,3 * 2 = 0,6
б) 0,8 * 3 = 2,4
в) 1,2 * 2 = 2,4
г) 2,3 * 3 = 6,9
д) 0,21 * 4 = 0,84
е) 1,6 * 5 = 8
ж) 3,7 * 10 = 37
з) 0,09 * 6 = 0,54
и) 0,18 * 5 = 0,9
к) 0,87 * 0 = 0
Задание 513
Догадайтесь, каковы корни уравнения:
а) 2,9x = 2,9;
б) 5,25x = 0;
в) 3,7x = 37;
г) x² = x;
д) a³ = a;
е) m² = m³.
Решение
а) 2,9x = 2,9
x = 1
6) 5,25x = 0
x = 0
в) 3,7x = 37
x = 10
г) х² = х
x = 1
д) a³ = a
a = 1
е) m² = m³
m = 1
Задание 514
Как изменится значение выражения 2,5а, если а:
увеличить на 1? увеличить на 2? увеличить в 2 раза?
Решение
Значение выражения 2,5а увеличится на 2,5:
2,5(a + 1) − 2,5a = 2,5a + 2,5 − 2,5a = 2,5.
Значение выражения 2,5a увеличится на 5:
2,5(a + 2) = 2,5a + 5 − 2,5a = 5;
Значение выражения 2,5a увеличится в 2 раза:
(2,5 * 2a) : 2,5a = 2.
Задание 515
Расскажите, как на координатном луче отметить число: 1/4 ; 3/4 ; 0,25 ; 0,5 ; 0,75.
Подумайте, какие из данных чисел равны.
Какой дроби со знаменателем 4 равны 0,5?
Сложите: 3/4 и 0,25; 1/4 и 0,15.
Решение
2/5 = 0,5
3/4 + 0,25 = 0,75 + 0,25 = 1
1/4 + 0,15 = 0,25 + 0,15 = 0,4.
Задание 516
Подумайте, по какому правилу составлен ряд чисел, и запишите ещё два числа этого ряда:
а) 1,2; 1,8; 2,4; 3; ...
б) 9,6; 8,9; 8,2; 7,5; ...
в) 0,9; 1,8; 3,6; 7,2; ...
г) 1,2; 0,7; 2,2; 1,4; 3,2; 2,1; ...
Решение
а) Каждое последующее число больше предыдущего на 0,6: 1,2; 1,8; 2,4; 3; 3,6; 4,2...
б) Каждое последующее число меньше предыдущего на 0,7: 9,6; 8,9; 8,2; 7,5; 6,8; 6,1...
в) Каждое последующее число больше предыдущего в 2 раза: 0,9; 1,8; 3,6; 7,2; 14,4; 28,8...
г) Каждое последующее число, стоящее на нечетном месте, больше предыдущего числа, стоящего на нечетном месте на 1; каждое число, стоящее на четном месте, больше предыдущего числа, стоящего на четном месте, на 0,7: 1,2; 0,7; 2,2; 1,4; 3,2; 2,1; 4,2; 2,8...
Задание 517
Выполните действия:
а) (37,8 − 19,1) * 4;
б) (14,23 + 13,97) * 31;
в) (64,37 + 33,21 − 21,56) * 14;
г) (33,56 − 18,29) * (13,2 + 24,9 − 38,1).
Решение
а) (37,8 − 19,1) * 4 = 74,8
б) (14,23 + 13,97) * 31 = 28,2 * 31 = 874,2
в) (64,37 + 33,21 − 21,56) * 14 = 76,02 * 14 = 1064,28
г) (33,56 − 18,29) * (13,2 + 24,9 − 38,1) = 15,27 − 0 = 0
Задание 518
Увеличьте каждое из чисел:
а) 3,705; 62,8; 0,5 в 10 раз;
б) 2,3578; 0,0068; 0,3 в 100 раз.
Решение
а) 3,705 * 10 = 37,05
62,8 * 10 = 628
0,5 * 10 = 5
б) 2,3578 * 100 = 235,78
0,0068 * 100 = 0,68
0,3 * 100 = 30
Задание 519
Округлите число 82719,364:
а) до единиц;
б) до сотен;
в) до десятых;
г) до сотых;
д) до тысяч.
Решение
а) 82719,364 ≈ 82719
б) 82 719,364 ≈ 82700
в) 82719,364 ≈ 82719,4
г) 82 719,364 ≈ 82719,36
д) 82719,364 ≈ 83000
Задание 520
Выполните действие:
а) 3 1/12 + 4 7/12;
б) 4 3/7 − 1 2/7;
в) 8 3/5 − 2/5;
г) 4/9 + 7 1/9.
Решение
а) 3112+4712=3+4+112+712=7812
б) 437−127=4−1+37−27=317
в) 835−25=815
г) 49+719=759
Задание 521
Сравните:
а) 2/11 + 7/11 и 4/11 + 6/11;
б) 8/13 − 3/13 и 9/13 − 4/13.
Решение
а) 211+711=911<411+611=1011
б) 813−313=513=913−413=513
Задание 522
Коля, Петя, Женя и Сеня взвесились на весах. Получились результаты: 37,7 кг; 42,5 кг; 39,2 кг; 40,8 кг. Найдите массу каждого мальчика, если известно, что Коля тяжелее Сени и легче Пети, а Женя легче Сени.
Решение
В порядке возрастания веса мальчики располагаются так:
Женя − 37,7 кг, Сеня − 39,2 кг, Коля − 40,8 кг и Петя − 42,5 кг.
Задание 523
Упростите выражение и найдите его значение:
а) 23,9 − 18,55 − m, если m = 1,64;
б) 16,4 + k + 3,8, если k = 2,7.
Решение
а) 23,9 − 18,55 − m = 5,35 − m;
при m = 1,64
5,35 − m = 5,35 − 1,64 = 3,71.
б) 16,4 + k + 3,8 = 20,2 + k;
при k = 2,7
20,2 + k = 20,2 + 2,7 = 22,9.
Задание 524
Решите уравнение:
а) 16,1 − (х − 3,8) = 11,3;
б) 25,34 − (2,7 + у) = 15,34.
Решение
а) 16,1 − (x − 3,8) = 11,3
x − 3,8 = 16,1 − 11,3 = 4,8
x = 4,8 + 3,8
х = 8,6
б) 25,34 − (2,7 + y) = 15,34
2,7 + y = 25,34 − 15,34 = 10
y = 10 − 2,7
у = 7,3
Задание 525
Найдите значение выражения:
1) (1070 − 104040 : 2312) * 74 + 6489;
2) (38529 + 205 * 87) : 427 − 119.
Решение
1) (1070 − 104040 : 2312) * 74 + 6489 = (1070 − 45) * 74 + 6489 = 1025 * 74 + 6489 = 75850 + 6489 = 82339
2) (38529 + 205 * 87) : 427 − 119 = (38529 + 17835) : 427 − 119 = 56364 : 427 − 119 = 132 − 119 = 13
Задание 526
Выполните деление:
а) 53,5 : 5;
б) 1,75 : 7;
в) 0,48 : 6;
г) 13,2 : 24;
д) 0,7 : 25;
е) 7,9 : 316;
ж) 543,4 : 143;
з) 40,005 : 127;
и) 9,607 : 10;
к) 14,706 : 1000;
л) 0,0142 : 100;
м) 0,75 : 10000.
Решение
а) 53,5 : 5 = 10,7
б) 1,75 : 7 = 0,25
в) 0,48 : 6 = 0,08
г) 13,2 : 24 = 0,55
д) 0,7 : 25 = 0,028
e) 7,9 : 316 = 0,025
ж) 543,4 : 143 = 3,8
з) 40,005 : 127 = 0,315
и) 9,607 : 10 = 0,9607
к) 14,706 : 1000 = 0,014706
л) 0,0142 : 100 = 0,000142
м) 0,75 : 10 000 = 0,000075
Задание 527
Автомашина шла по шоссе 3 ч со скоростью 65,8 км/ч, а затем 5 ч она шла по грунтовой дороге. С какой скоростью она шла по грунтовой дороге, если весь её путь равен 324,9 км?
Решение
(324,9 − 65,8 * 3) : 5 = 127,5 : 5 = 25,5 (км/ч) - скорость машины по грунтовой дороге
Овет: 25,5 км/ч.
Задание 528
На складе было 180,4 т угля. Для отопления школ отпущено 3/11 этого угля. Сколько тонн угля осталось на складе?
Решение
1) 180,4 : 11 * 3 = 16,4 * 3 = 49,2 (т) - угля было отпущено на отопление
2) 180,4 − 49,2 = 131,2 (т ) - угля осталось на складе
Ответ: 131,2 т.
Задание 529
Вспахали 5/7 поля. Найдите площадь этого поля, если вспахали 32,5 га.
Решение
32,5 : 5 * 7 = 6,5 * 7 = 45,5 (га) - площадь всего поля равна
Ответ: 45,5 га.
Задание 530
Решите уравнение:
а) 15x = 0,15;
б) 3,08 : у = 4;
в) 3a + 8a = 1,87;
г) 72 − 3z = 5,12;
д) 2t + 5t + 3,18 = 25,3;
е) 8p − 2p − 14,21 = 75,19;
ж) 295,1 : (n − 3) = 13;
з) 34 * (m + 1,2) = 61,2;
и) 15 * (k − 0,2) = 21.
Решение
а) 15x = 0,15
x = 0,15 : 15
х = 0,01
б) 3,08 : у = 4
у = 3,08 : 4
у = 0,77
в) 3a + 8a = 1,87
a = 1,87 : 11
а = 0,17
г) 72 − 3z = 5,12
z = 5,12 : 4
z = 1,28
д) 2t + 5t + 3,18 = 25,3
t = (25,3 − 3,18) : 7
t = 3,16
е) 8p − 2p − 14,21 = 75,19
p = (75,19 + 14,21) : 6
p = 14,9
ж) 295,1 : (n − 3) = 13
n = 295,1 : 13 + 3
n = 25,7
з) 34 * (m + 1,2) = 61,2
m = 61,2 : 34 − 1,2
m = 0,6
и) 15 * (k − 0,2) = 21
k = 21 : 15 + 0,2
k = 1,6
Задание 531
Найдите значение выражения:
а) 0,24 : 4 + 15,3 : 5 + 12,4 : 8 + 0,15 : 30;
б) (1,24 + 3,56) : 16;
в) 2,28 + 3,72 : 12;
г) 3,6 + 2,4 : (11,7 − 3,7).
Решение
а) 0,25 : 4 + 15,3 : 5 + 12,4 : 8 + 0,15 : 30 = 0,0625 + 3,06 + 1,55 + 0,005 = 4,6775
б) (1,24 + 3,56) : 16 = 4,8 : 16 = 0,3
в) 2,28 + 3,72 : 12 = 2,28 + 0,31 = 2,59
г) 3,6 + 2,4 : (11,7−3,7) = 3,6 + 2,4 : 8 = 3,6 + 0,3 = 3,9
Задание 532
С трёх лугов собрали 19,7 т сена. С первого и второго лугов собрали сена поровну, а с третьего собрали на 1,1 т больше, чем с каждого из первых двух. Сколько сена собрали с каждого луга?
Решение
Пусть с каждого из первых двух лугов собрали х т сена,
тогда с третьего луга собрали (х + 1,1) т сена.
Составим уравнение:
х + х + (х + 1,1) = 19,7
х = (19,7 − 1,1) : 3
х = 6,2
Значит, 6,2 т сена собрали с первого и столько же со второго луга.
х + 1,1 = 7,3 (т) - собрали с третьего луга
Ответ: 6,2 т, 6,2 т, 7,3 т.
Задание 533
Магазин за 3 дня продал 1240,8 кг сахара. В первый день было продано 543 кг, во второй − в 2 раза больше, чем в третий. Сколько килограммов сахара продано в третий день?
Решение
Пусть в третий день продали х кг сахара,
тогда во второй день продали 2х кг.
Составим уравнение:
543 + 2х + х = 1240,8
х = (1240,8 − 543) : 3
х = 232,6
Значит, 232,6 кг сахара было продано в третий день.
Ответ: 232,6 кг.
Задание 534
Машина прошла первый участок пути за 3 ч, а второй участок − за 2 ч. Длина обоих участков вместе 267 км. С какой скоростью шла машина на каждом участке, если скорость на втором участке была на 8,5 км/ч больше, чем на первом?
Решение
Пусть скорость машины на первом участке была х км/ч,
тогда на втором участке (х + 8,5) км/ч.
Составим уравнение:
3х + 2 * (х + 8,5) = 267
3х + 2х + 17 = 267
х = (267 − 17) : 5
х = 50
Значит, 50 км/ч − скорость машины на первом участке
50 + 8,5 = 58,5 (км/ч) - её скорость на втором участке
Ответ: 50 км/ч, 58,5 км/ч.
Задание 535
Обратите в десятичные дроби: 9/20 ; 7/40 ; 11/400 ; 21/168 ; 35/280 ; 47/367.
Решение
9/20 = 45/100 = 0,45
7/40 = 175/1000 = 0,175
11/400 = 275/10000 = 0,0275
21/168 = 1/8 = 125/1000 = 0,125
35/280 = 1/8 = 125/1000 = 0,125
47/376 = 1/8 = 125/1000 = 0,125
Задание 536
Постройте фигуру, равную фигуре, изображённой на рисунке 151.
Решение
Площадь данной фигуры 28 клеток, значит равновеликой может быть например любая фигура из 28 клеток.
Задание 537
Из города выехал велосипедист со скоростью 13,4 км/ч. Через 2 ч вслед за ним выехал другой велосипедист, скорость которого 17,4 км/ч. Через сколько часов после своего выезда второй велосипедист догонит первого?
Решение
(13,4 * 2) : (17,4 − 13,4) = 26,8 : 4 = 6,7 (ч) - через столько после своего выезда второй велосипедист догонит первого
Ответ: через 6,7 ч.
Задание 538
Катер, двигаясь против течения, за 6 ч прошёл 177,6 км. Найдите собственную скорость катера, если скорость течения равна 2,8 км/ч.
Решение
177,6 : 6 + 2,8 = 29,6 + 2,8 = 32,4 (км/ч) - собственная скорость катера
Ответ: 32,4 км/ч.
Задание 539
Кран, который подаёт в минуту 30 л воды, за 5 мин наполнил ванну. Потом кран закрыли и открыли сливное отверстие, через которое вся вода вылилась за 6 мин. Сколько литров воды выливалось за 1 мин?
Решение
1) 30 * 5 = 150 (л) - воды налилось в ванну
2) 150 : 6 = 25 (л) - воды выливалось за 1 минуту
Ответ: 25 л.
Задание 540
Решите уравнение:
а) 26 * (х + 427) = 15756;
б) 101 * (351 + у) = 65549;
в) 22 374 : (k − 125) = 1243;
г) 38 007 : (4223 − t) = 9.
Решение
а) 26 * (х + 427) = 15 756
x = 15 756 : 26 − 427
х = 606 − 427
х = 179
б) 101 * (351 + у) = 65549
у = 65549 : 101 − 351
у = 649 − 351
у = 298
в) 22 374 : (k − 125) = 1243
k = 22374 : 1243 + 125
k = 18 + 125
k = 143
г) 38007 : (4223 − t) = 9
t = 4223 − 38007 : 9
t = 4223 − 4223
t = 0


