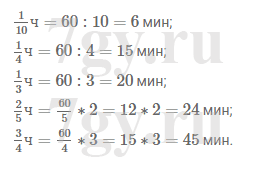Ответы к пункту 25. Правильные и неправильные дроби, стр. 27

Задание № 125

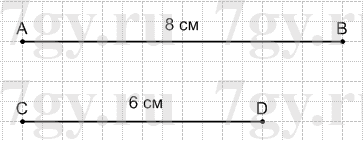
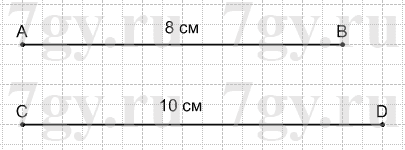
Длина отрезка АВ равна 8 см. Начертите отрезок, длина которого равна:
а) 3/4 длины отрезка АВ;
б) 5/4 длины отрезка АВ.

Решение

а)

б)

Задание № 126

Отметьте на луче точки с координатами: 1/4;2/4;3/4;4/4;5/4;6/4;7/4;8/4.
За единичный отрезок примите длину 12 клеток тетради.

Решение

Задание № 127

Напишите:
а) все правильные дроби со знаменателем 6;
б) все неправильные дроби с числителем 5.

Решение

а) $\frac16,\frac26,\frac36,\frac46,\frac56$

б) $\frac51,\frac52,\frac53,\frac54,\frac55$

Задание № 128

При каких значениях а дробь:
а) a/10 будет правильной;
б) 16/a будет неправильной?

Решение

При а = 1, 2, 3, 4, 5, 6, 7, 8, 9 дробь a/10 является правильной
При а = 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16 дробь 16/a является неправильной.

Задание № 129

Машина за 6 мин может вырыть канаву длиной в 1 м.
Какой длины канаву выроет машина за 1 мин; 5 мин; 7 мин; 11 мин?

Решение

Задание № 130

Одним килограммом краски можно покрасить 5 м² поверхности.
Сколько понадобится краски, чтобы покрасить 3 м²; 6 м²; 13 м² поверхности?

Решение

Задание № 131

Бригада строителей построила ферму за 48 дней. По плану требовалось 5/4 этого времени. Сколько дней отводилось на постройку фермы по плану?

Решение

48 : 4 * 5 = 12 * 5 = 60 (д.)
Ответ: 60 дней отводилось на постройку фермы по плану.

Задание № 132

Токарь за 3 ч выточил на токарном станке 135 деталей, выполнив 3/5 дневной нормы. Сколько деталей он должен был выточить за рабочий день (8 часов) по норме? Сколько деталей он выточит за рабочий день, если будет работать с той же производительностью?

Решение

1) 135 : 3 * 5 = 45 * 5 = 225 (д.) - дневная норма токаря
2) 135 : 3 = 45 (д.) - вытачивает токарь за 1 ч
3) 45 * 8 = 360 (д.) - сделает токарь за 8 ч
Ответ: 360 деталей.

Задание № 133

Токарь выточил на токарном станке 135 деталей, выполнив 27/20 дневной нормы. Какова его дневная норма?

Решение

135 : 27 * 20 = 5 * 20 = 100 (д)
Ответ: 100 деталей - дневная норма токаря.

Задание № 134

Концерт юных музыкантов вместо запланированных 3 ч продолжался 13/10 этого времени, так как зрители просили повторить некоторые понравившиеся выступления. Сколько времени продолжался концерт? Сколько минут продолжались выступления на бис?

Решение

1) 3 * 60 : 10 * 13 = 18 * 13 = 234 (мин) - продолжался концерт
234 (мин) = 3 ч 54 мин
2) 3 ч 54 мин - 3 ч = 54 мин - продолжалось выступление на бис
Ответ: 3 ч 54 мин, 54 мин.

Задание № 135

Вычислите устно:
а) 400 : 25
* 5
+ 40
: 12
+ 190
?
б) 700 - 20
: 4
* 2
: 17
+ 480
?
в) 420 : 14
* 6
+ 120
: 25
* 8
?
г) 320 + 240
: 80
* 50
- 60
: 29
?

Решение

а) 16, 80, 120, 10, 200.
б) 680, 170, 340, 20, 500.
в) 30, 180, 300, 12, 96.
г) 560, 7, 350, 290, 10.

Задание № 136

Сколько минут в часе? Какую часть часа составляет 1 мин; 7 мин; 15 мин?

Решение

1 ч = 60 мин, 1 мин = 1/60 ч, 7 мин = 7/60 ч, 15 мин = 15/60 ч.

Задание № 137

Во сколько раз центнер больше килограмма? Какую часть центнера составляет килограмм? На сколько центнер больше килограмма?

Решение

1 ц = 100 кг,
100 кг : 1 кг = 100,
1 кг = 1/100 ц,
1 ц − 1 кг = 100 кг − 1 кг = 99 кг.

Задание № 138

Сколько минут:
в 1/10 ч;в 1/4 ч;в 1/3 ч;в 2/5 ч;в 3/4 ч?

Решение

Задание № 139

Сложите 2/5 числа 40 и 2/3 числа 60.
Из 5/6 числа 72 вычтите 2/9 числа 81.

Решение

Задание № 140

Половина числа равна 18. Найдите это число. Треть числа равна 27. Найдите это число. Три четверти числа равны 60. Найдите это число.

Решение

18 * 2 = 36
27 * 3 = 81
60 : 3 * 4 = 80

Задание № 141

Какая часть четырёхугольника ABCD (рис. 125) закрашена? Какая часть осталась незакрашенной?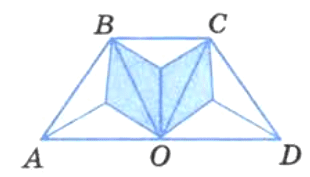

Решение

Закрашено 4/9 четырехугольника ABCD, осталось не закрашено 5/9 четырехугольника.

Задание № 142

Выразите в граммах:
а) 3 кг 400 г;
б) 2 кг 30 г;
в) 15 кг.

Решение

a) 3 кг 400 г = 3400 г
б) 2 кг 30 г = 2030 г
в) 15 кг = 15000 г

Задание № 143

Расположите в порядке возрастания дроби:4/11;2/11;10/11;9/11;8/11;7/11.
Расположите эти же дроби в порядке убывания.

Решение

В порядке возрастания: $\frac2{11}<\frac4{11}<\frac7{11}<\frac8{11}<\frac9{11}<\frac{10}{11}$
В порядке убывания: $1\frac{10}{11}>\frac9{11}>\frac8{11}>\frac7{11}>\frac4{11}>\frac2{11}$

 

Задание № 144

Назовите четыре дроби, которые меньше, чем 1/1000000.

Решение

$\frac1{1100000}<\frac1{1010000}<\frac1{1001000}<\frac1{1000100}<\frac1{1000000}$

Задание № 145

Назовите 5 дробей, которые больше, чем 1/9.

Решение

$\frac69>\frac59>\frac49>\frac39>\frac29>\frac19$

Задание № 146

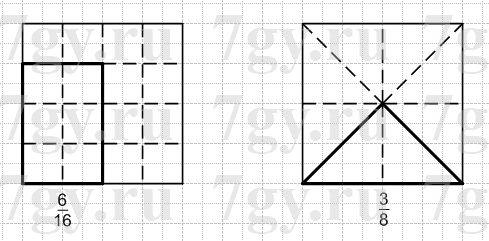
Начертите квадрат со стороной 4 см. Покажите на чертеже: 6/16 квадрата, 3/8 квадрата. Найдите площади этих частей квадрата и объясните полученный результат.

Решение

$S_{квадрата}=4\ast4=16\;(см^2)$
$16\ast6:16=6\;(см^2)$ - площадь 6/16 квадрата;
$16\ast3:8=6\;(см^2)$ - площадь 3/8 квадрата.

Задание № 147

В первый день бригада собрала 5 т 400 кг картофеля, а во второй − на 1 т 200 кг меньше, чем в первый. В третий день бригада собрала в 2 раза больше картофеля, чем во второй. Сколько картофеля собрано бригадой за эти три дня?

Решение

1) 5 т 400 кг − 1 т 200 кг = 5400 кг − 1200 кг = 4200 кг картофеля собрала бригада во второй день
2) 2 * 4200 = 8400 (кг) - картофеля собрала бригада в третий день
3) 5400 + 4200 + 8400 = 18000 (кг) = 18 (т) - картофеля собрала бригади за 3 дня
Ответ: 18 т картофеля.

Задание № 148

Составьте задачу по уравнению:
а) (у + 6) − 2 = 15;
б) 2(a − 5) = 24;
в) 3(25 + b) + 15 = 135.

Решение

а) У Вити было на 6 рублей больше чем у Пети. Сколько рублей было у Пети, если у Вити, истратившего 2 рубля осталось 15 рублей.
Пусть у Пети было y рублей, тогда у Пети было у + 6 рублей.
Составим уравнение:
(у + 6) − 2 = 15
у + 4 = 15
y = 15 − 4 = 11 (р.) - было у Пети

б) Скорость первого велосипедиста на 5 км/ч меньше скорости второго велосипедиста. Найдите скорость второго велосипедиста, если первый велосипедист за 2 часа проехал 24 км.
Пусть скорость второго велосипедиста равна а км/ч, тогда скорость первого велосипедиста равна (а − 5) км/ч.
Составим уравнение:
2(a − 5) = 24
2a − 10 = 24
2a = 24 + 10 = 34
a = 34 : 2 = 17 (км/ч) - скорость второго велосипедиста

в) Расстояние между селом и городом равно 135 км. Найдите скорость мотоцикла, если известно, что автомобиль, выехавший из села со скоростью на 25 км/ч больше скорости мотоцикла, через три часа не доехал до города 15 км.
Пусть скорость мотоцикла равна b км/ч, тогда скорость автомобиля равна (25 + b) км/ч.
Составим уравнение:
3(25 + b) + 15 = 135
75 + b + 15 = 135
b = 135 − 75 − 15 = 45 (км/ч) - скорость мотоцикла

Задание № 149

В первом вагоне ехали а человек, а во втором − b человек. На остановке из первого вагона вышли с человек, а из второго − d человек. Какой смысл имеют следующие выражения:
a + b; с + d; (a + b) − (с + d);
a − с; b − d; (a − с) + (b − d)?
Объясните, почему
(a + b) − (c + d) = (a − c) + (b − d) при а > с, b > d.
Проверьте это равенство при а = 45, b = 39, с = 14, d = 12.
Используя полученное равенство, вычислите значение выражения:
а) (548 + 897) − (148 + 227);
б) (391 + 199) − (181 + 79).

Решение

a + b − число пассажиров в первом и втором вагонах,
с + d − общее число вышедших пассажиров,
(a + b) − (с + d) − число оставшихся пассажиров в первом и втором вагонах,
a − с − число пассажиров оставшихся в первом вагоне,
b − d − число пассажиров оставшихся во втором вагоне;
(a − с) + (b − d) = a − c + b − d = (a + b) − (с + d).
Если a = 45, b = 39, с = 14, d = 12,
(a + b) − (с + d) = (45 + 39) − (14 + 12) = 84 − 26 = 58;
(a − c) + (b − d) = (45 − 14) + (39 − 12) = 31 + 27 = 58.

а) (548 + 897) − (148 + 227) = (548 − 148) + (897 − 227) = 400 + 670 = 1070
б) (391 + 199) − (181 + + 79) = (391 − 181) + (199 − 79) = 210 + 120 = 330

Задание № 150

Придумайте пять дробей, у которых числитель на 3 меньше знаменателя. Запишите пять дробей, у которых числитель в 3 раза больше знаменателя.

Решение

$\frac47,\frac58,\frac69,\frac7{10},\frac8{11}$
$\frac62,\frac93,\frac{12}4,\frac{15}5,\frac{18}6$

Задание № 151

При каких значениях х дробь 8/х будет неправильной?

Решение

При х от 1 до 8 дробь 8/х будет неправильной.

Задание № 152

Фермер наметил собрать с поля 12 т овощей, а собрал 7/6 этого количества. Сколько тонн овощей собрал фермер?

Решение

12 : 6 * 7 = 2 * 7 = 14 (т)
Ответ: 14 т овощей собрал фермер.

Задание № 153

Турист прошёл за первый день 18 км, что составляет 6/5 пути, который он должен пройти во второй день. Сколько километров должен пройти турист за эти два дня?

Решение

1) 18 : 6 * 5 = 3 * 5 = 15 (км) - должен пройти турист за второй день
2) 18 + 15 = 33 (км) - должен пройти турист за два дня
Ответ: 33 км.

Задание № 154

Из Санкт−Петербурга в Москву вышел товарный поезд со скоростью 48 км/ч, а через час после этого из Москвы в Санкт−Петербург вышел скорый поезд со скоростью 82 км/ч. Найдите расстояние между поездами:
а) через 1 ч после выхода скорого поезда;
б) через 3 ч после выхода товарного поезда;
в) через 5 ч после выхода скорого поезда.
Расстояние от Москвы до Санкт−Петербурга 650 км.

Решение

a) 650 − (48 * 1 + (82 + 48 * 1) = 650 − (48 + 130) = 650 − 178 = 472 км
б) 650 − (48 * 3 + 82 * 2) = 650 − (144 + 164) = 650 − 308 = 342 км
в) 48 * 6 + 82 * 5 − 650 = 288 + 410 − 650 = 698 − 650 = 48 км

Задание № 155

Найдите значение выражения:
а) 8060 * 45 − 45 150 : 75 * 105;
б) (2 254 175 + 94 447) : 414 − 1329;
в) (12³−9³):(12−9);
г) (6²+3²)².

Решение

а) 8060 * 45 − 45 150 : 75 * 105 = 362700 − 602 * 105 = 362700 − 63210 = 299490

б) (2254175 + 94447) : 414 − 1329 = 2348622 : 414 − 1329 = 5673 − 1329 = 4344

в) $(12^3-9^3):(12-9)=(144\ast12-81\ast9):3=999:3=333$

г) $(6^2+3^2)^2=(36+9)^2=452=2025$