Пункт 32. Ответы к теме Сложение и вычитание десятичных дробей, страница 73

Задание 361

На пальто израсходовали 3,2 м ткани, а на костюм − 2,63 м. Сколько ткани израсходовали на пальто и костюм вместе? Решите задачу сложением десятичных дробей и путём перехода к сантиметрам.

Решение

1способ
3,2 + 2,63 = 5,83 (м) - ткани было израсходовано на пальто и костюм
Ответ: 5,83 м.
2 способ
3 м 20 см + 2 м 63 см = 320 см + 263 см = 583 см = 5 м 83 см - ткани было израсходовано на пальто и костюм
Ответ: 5 м 83 см.

Задание 362

Масса автомобиля «Нива» 11,5 ц, а масса автомобиля «Волга» 14,2 ц. На сколько масса «Волги» больше массы «Нивы»? Решите задачу с помощью десятичных дробей и переводом данных в килограммы.

Решение

14,2 − 11,5 = на 2,7 (ц) - масса «Волги» больше массы «Нивы»
14 ц 20 кг − 11 ц 50 кг = 1420 кг − 1150 кг = 270 кг = 2 ц 70 кг
Ответ: на 2,7 ц или  2 ц 70 кг.

Задание 363

Выполните сложение:
а) 0,769 + 42,389;
б) 5,8 + 22,191;
в) 95,381 + 3,219;
г) 8,9021 + 0,68;
д) 2,7 + 1,35 + 0,8;
е) 13,75 + 8,2 + 0,115.

Решение

а) 
+ 0.769
 42.389
 43.158

б)
+ 5.8
 22.191
 27.991

в)
+ 95.381
     3.219
   98.6

г)
+ 8.9021
   0.68    
   9.5821

д)
+ 2.7
   1.35
   0.8  
   4.85

е)
+ 13.75
     8.2
     0.115
   22.065

Задание 364

Выполните вычитание
а) 9,4 − 7,3;
б) 16,78 − 5,48;
в) 7,79 − 3,79;
г) 11,1 − 2,8;
д) 88,252 − 4,69;
е) 6,6 − 5,99.

Решение

а) 
- 9.4
  7.3
  2.1

б)
- 16.78
    5.48
  11.3

в)
- 7.79
  3.79
  4

г)
- 11.1
    2.8
    8.3

д)
- 88.252
    4.69  
  83.562

е)
- 6.6
  5.99
  0.61

Задание 365

С одного участка собрали 95,37 т зерна, а с другого − на 16,8 т больше. Сколько тонн зерна собрали с двух участков?

Решение

 95,37 + (95,37 + 16,8) = 95,37 + 112,17 = 307,54 (т) - собрали с двух участков
Ответ: 307,54 т.

Задание 366

Один тракторист вспахал 13,8 га земли, что оказалось на 4,7 га меньше, чем вспахал второй тракторист. Сколько гектаров земли вспахали оба тракториста вместе?

Решение

 13,8 + (13,8 + 4,7) = 13,8 + 18,5 = 32,3 (га) - вспахали оба тракториста
Ответ: 32,3 га.

Задание 367

От куска провода длиной 30 м отрезали 4,75 м. Сколько метров провода осталось в куске?

Решение

 30 − 4,75 = 25,25 (м) - провода осталось в куске
Ответ: 25,25 м.

Задание 368

Груз, поднимаемый вертолётом, легче вертолёта на 4,72 т. Какова масса вертолёта вместе с грузом, если масса груза 1,24 т?

Решение

(4,72 + 1,24) + 1,24 = 5,96 + 1,24 = 7,2 т - масса вертолёта вместе с грузом
Ответ: 7,2 т.

Задание 369

Выполните действие:
а) 7,8 + 6,9;
б) 129 + 9,72;
в) 8,1 − 5,46;
г) 96,3 − 0,081;
д) 24,2 + 0,867;
е) 830 − 0,0097;
ж) 0,02 − 0,0156;
з) 0,003 − 0,00089;
и) 1 − 0,999;
к) 425 − 2,647;
л) 83 − 82,877;
м) 37,2 − 0,03.

Решение

а) 
+ 7.8
   6.9
 14.7

б)
+ 129
       9.72
   138.72

в)
- 8.1
  5.46
  2.64

г)
- 96.3
    0.081
  96.219

д)
+ 24.2
     0.867
   25.067

е)
- 830
      0.0097
  829.9903

ж)
- 0.02
  0.0156
  0.0044

з)
- 0.003
  0.00089
  0.00211

и)
- 1
  0.999
  0.001

к)
- 425
      2.647
  422.353

л)
- 83
  82.877
    0.123

м)
- 37.2
    0.03
  37.17

Задание 370

Собственная скорость катера (скорость в стоячей воде) равна 21,6 км/ч, а скорость течения реки 4,7 км/ч. Найдите скорость катера по течению и против течения.

Решение

1)  21,6 + 4,7 = 3 (км/ч) - корость катера по течению реки
2) 21,6 − 4,7 = 16,9 (км/ч) - скорость катера против течения
Ответ: 3 км/ч, 16,9 км/ч

Задание 371

Скорость теплохода по течению равна 37,6 км/ч. Найдите собственную скорость теплохода и его скорость против течения, если скорость течения реки 3,9 км/ч.

Решение

1) 37,6 − 3,9 = 33,7 (км/ч) - собственная скорость теплохода
2) 33,7 − 3,9 = 29,8 (км/ч) - скорость теплохода против течения
Ответ: 33,7 км/ч, 29,8 км/ч.

Задание 372

Скорость велосипедиста 15 км/ч, а скорость пешехода на 9,7 км/ч меньше. На сколько уменьшится расстояние между ними за 1 ч, если они движутся навстречу друг другу? На сколько увеличивается расстояние между ними за 1 ч, если они движутся из одной точки в противоположные стороны?

Решение

1) 15 − 9,7 = 5,3 (км/ч) - скорость пешехода
2) 15 + 5,3 = 20,3 (км/ч) - скорость сближения и скорость удаления
Значит, расстояние между ними за 1 час уменьшится на 20,3 км,  если они движутся навстречу друг другу, и увеличится на 20,3 км, если они движутся из одной точки в противоположные стороны.
Ответ:  на 20,3 км.

Задание 373

Расстояние между городами 156 км. Из них навстречу друг другу выехали два велосипедиста. Один проезжает в час 13,6 км, а второй − 10,4 км. Через сколько часов они встретятся?

Решение

(13,6 + 10,4) = 24 (км/ч) - скорость сближения велосипедистов
$156:24=\frac{156}{24}=6\frac12$ (ч) - время, через которое они встретятся
Ответ: через $6\frac12$ ч.

Задание 374

Верёвку разрезали на пять кусков. Первый кусок больше второго на 4,2 м, но меньше третьего на 2,3 м. Четвёртый кусок больше пятого на 3,7 м, но меньше третьего на 1,3 м. Какова длина веревки, если длина четвёртого куска 7,8 м?

Решение

1) 7,8 + 1,3 = 9,1 (м) - длина третьего куска
2) 7,8 − 3,7 = 4,1 (м) - длина пятого куска
3) 9,1 − 2,3 = 6,8 (м) - длина первого куска
4) 6,8 − 4,2 = 2,6 (м) - длина второго куска
5) 6,8 + 2,6 + 9,1 + 7,8 + 4,1 = 30,4 (м) -  длина верёвки
Ответ: 30,4 м.

Задание 375

Найдите периметр треугольника ABC, если АВ = 2,8 см, ВС больше АВ на 0,8 см, но меньше АС на 1,1 см.

Решение

ВС = 2,8 + 0,8 = 3,6 см
АС = 3,6 + 1,1 = см
РАВС = 2,8 + 3,6 + 4,7 = 6,4 + 4,7 = 11,1 см

Задание 376

Используя буквы х и у, запишите переместительное свойство сложения и проверьте его, если х = 7,3, а у = 29.
Используя буквы a, b и с, запишите сочетательное свойство сложения и проверьте его при а = 2,3; b = 4,2 и с = 3,7.

Решение

x + у = у + x,
при x = 7,3, у = 29
х + у = 7,3 + 29 = 36,3;
y + x = 29 + 7,3 = 36,3.
Выражение верно.

(a + b) + с = a + (b + с),
при a = 2,3; b = 4,2; c = 3,7
(a + b) + с = (2,3 + 4,2) + 3,7 = 6,5 + 3,7 = 10,2;
a + (b + с) = 2,3 + (4,2 + 3,7) = 2,3 + 7,9 = 10,2.
Выражение верно.

Задание 377

Используя буквы a, b и с, запишите свойство вычитания числа из суммы и свойство вычитания суммы из числа.
Проверьте эти свойства при a = 13,2; b = 4,8 и с = 2,7.

Решение

(a + b) − с = a + (b − с),
при a = 13,2; b = 4,8; с = 2,7:
(a + b ) − c = (13,2 + 4,8) − 2,7 = 18 − 2,7 = 15,3;
a + (b − с) = 13,2 + (4,8 − 2,7) = 13,2 + 2,1 = 15,3.

a − (b + с) = a − b − c,
при а = 13,2; b = 4,8; c = 2,7:
a − (b + c) = 13,2 − (4,8 + 2,7) = 13,2 − 7,5 = 5,7;
a − b − c = 13,2 − 4,8 − 2,7 = 8,4 − 2,7 = 5,7.

Задание 378

Используя свойства сложения и вычитания, вычислите самым удобным способом значение выражения:
а) 2,31 + (7,65 + 8,69);
б) 0,387 + (0,613 + 3,142);
в) (7,891 + 3,9) + (6,1 + 2,109);
г) 14,537 − (2,237 + 5,9);
д) (24,302 + 17,879) − 1,302;
е) (25,243 + 17,77)− 2,77.

Решение

а) 2,31 + (7,65 + 8,69) = (2,31 + 8,69) + 7,65 = 11 + 7,65 = 18,65

6) 0,387 + (0,613 + 3,142) = (0,387 + 0,613) + 3,142 = 1 + 3,142 = 4,142

в) (7,891 + 3,9) + (6,1 + 2,109) = (7,891 + 2,109) + (3,9 + 6,1) = 10 + 10 = 20

г) 14,537 − (2,237 + 5,9) = (14,537 − 2,237) − 5,9 = 12,3 − 5,9 = 6,4

д) (24,302 + 17,879) − 1,302 = (24,302 − 1,302) + 17,879 = 23 + 17,879 = 40,879

e) (25,243 + 17,77) − 2,77 = 25,243 + (17,77 − 2,77) = 25,243 + 15 = 40,243

Задание 379

Выполните действия:
а) 9,83 − 1,76 − 3,28 + 0,11;
б) 12,371 − 8,93 + 1,212;
в) 14,87 − (5,82 − 3,27);
г) 14 − (3,96 + 7,85).

Решение

а) 9,83 − 1,76 − 3,28 + 0,11 = (9,83 + 0,11) − (1,76 + 3,28) = 9,94 − 5,04 = 4,9

б) 12,371 − 8,93 + 1,212 = 3,441 + 1,212 = 4,653

в) 14,87 − (5,82 − 3,27) = 14,87 − 2,55 = 12,32

г) 14 − (3,96 + 7,85) = 14 − 11,81 = 2,19

Задание 380

Сколько единиц в каждом разряде числа: 32,547; 2,6034?

Решение

Число 32,547:
в разряде десятков 3 единицы, в разряде единиц − 2, в разряде десятых − 5,
в разряде сотых − 4, в разряде тысячных − 7. Число 2,6034:
в разряде единиц − 2, в разряде десятых − 6, в разряде сотых − 0,
в разряде тысячных − З, в разряде десятитысячных − 4.

Задание 381

==

Решение

а) 24, 578
   20 + 4 + 0,5 = 0,07 + 0, 008 = 24, 578

б) 0,520001
    0,5 + 0,02 + 0,000001 = 0,520001

Задание 382

Разложите по разрядам число:
а) 24,578;
б) 0,520001.

Решение

а) 24,578 = 20 + 4 + 0,5 + 0,07 + 0,008

б) 0,520001 = 0,5 + 0,02 + 0,000001

Задание 383

Запишите десятичную дробь, в которой:
а) 15 целых, 3 десятых, 7 сотых и 9 тысячных;
б) 0 целых, 3 десятых, 0 сотых и 4 тысячных.

Решение

а) 15,379

б) 0,304

Задание 384

Выразите длину отрезка АВ = 5 м 7 дм 6 см 2 мм:
а) в метрах;
б) в дециметрах;
в) в сантиметрах;
г) в миллиметрах.
Выразите длину отрезка СМ в метрах, дециметрах, сантиметрах и миллиметрах, если СМ = 4,573 м.

Решение

а) 5 м 7 дм 6 см 2 мм = 5 м + 0,7 м +0,06 м + 0,002 м = 5,762 м

б) 5 м 7 дм 6 см 2 мм = 50 дм + 7 дм + 0,6 дм + 0,02 дм = 57,62 дм

в) 5 м 7 дм 6 см 2 мм = 500 см + 70 см + 6 см + 0,2 см = 576,2 см

г) 5 м 7 дм 6 см 2 мм = 5000 мм + 700 мм + 60 мм + 2 мм = 5762 мм

СМ = 4,573 м = 45,73 дм = 457,3 см = 4573 мм

 

Задание 385

Найдите координаты точек А, В, С, D и К (рис. 146).

Решение

A(5,3), B(5,8), С(6,2), D(6,6), K(6,8).

Задание 386

Зная, что 11,87 − 7,39 = 4,48, найдите значение выражения или решите уравнение:
а) 7,39 + 4,48;
6) 11,87 − 4,48;
в) х − 7,39 = 4,48;
г) 7,39 + у = 11,87;
д) 4,48 + z = 11,87;
е) 11,87 − р = 7,39.

Решение

а) 7,39 + 4,48 = 11,87

б) 11,87 − 4,48 = 7,39

в) х − 7,39 = 4,48
х = 4,48 + 7,39
х = 11,38

г) 7,39 + у = 11,87
у = 11,87 − 7,39
у = 4,48

д) 4,48 + z = 11,87
z = 11,87 − 4,48
z = 7,39

е) 11,87 − р = 7,39
р = 11,87 − 7,39
р = 4,48

Задание 387

Прочитайте показания термометров (рис. 147). Сколько градусов будет показывать каждый из них, если его столбик:
а) поднимется на 4 малых деления; на 2 больших деления; на 0,5°С; на 1,3 °С;
б) опустится на 7 малых делений; на одно большое деление; на 0,3°С; на 1,4 °С?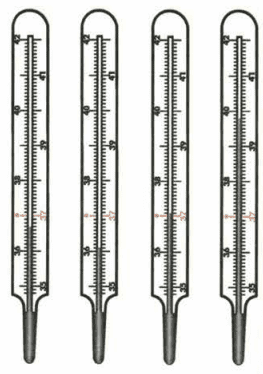

Решение

Термометр 1 показывает температуру 36,7°С, термометр 2 − 36,1°С, термометр 3 − 37,1°С, термометр 4 − 39,8°С.

а) Если температура поднимется на 4 малых деления, то термометры покажут:
1 − 37,1°С, 2 − 3б,5°С, 3 − 37,5°C, 4 − 40,2°C;
если температура поднимется на 2 больших деления, то термометры покажут:
1 − 38,7°С, 2 − 38,1°С, 3 − 39,1°С, 4 − 41,8°С;
если температура поднимется на 0,5°С, то термометры покажут:
1 − 37,2°С, 2 − 36,6°С, 3 − 37,б°С, 4 − 40,3°С,
если температура поднимется на 1,3°С, то термометры покажут:
1 − 38°С, 2 − 37,4°С, 3 − 38,4°С, 4 − 41,1°С.

б) Если температура опустится на 7 малых делений, то термометры покажут:
1 − 36°С, 2 − 35,4°С, 3 − 3б,4°С, 4 − 39,1°С;
если температура опустится на 1 большое деление, то термометры покажут:
1 − 35,7°С, 2 − 35,1°С, 3 − 36,1°С, 4 − 38,8°С;
если температура опустится на 0,3°С, то термометры покажут:
1 − 36,4°С, 2 − 35,8°С, 3 − −3б,8°С, 4 − 39,5°С;
если температура опустится на 1,4°С, то термометры покажут:
1 − 35,3°С, 2 − 34,7°С, 3 − 35,7°С, 4 − 38,4°С.

Задание 388

Решите уравнение:
а) z + 3,8 = 8;
б) у − 6,5 = 12;
в) 13,5 − х = 1,8;
г) 15,4 + k = 15,4;
д) 2,8 + l + 3,7 = 12,5;
е) (5,6 − r) + 3,8 = 4,4.

Решение

а) z + 3,8 = 8
z = 8 − 3,8
z = 4,2

б) у − 6,5 = 12
у = 12 + 6,5
у = 18,5

в) 13,5 − x − 1,8
х = 13,5 − 1,8
х = 11,7

г) 15,4 + k = 15,4
k = 15,4 − 15,4
k = 0

д) 2,8 + z + 3,7 = 12,5
z = 12,5 − 6,5
z = 6

е) (5,6 − r) + 3,8 = 4,4
r = 5,6 − 0,6
r = 5

Задание 389

Вычислите устно:
а) 60 - 36
* 3
: 4
+ 27
: 3
?
б) 55 + 25
: 5
+ 7
* 3
+ 31
?
в) 75 : 25
* 15
: 9
* 12
+ 240
?
г) 15 * 6
- 39
: 17
* 18
+ 46
?
д) 45 + 30
: 15
* 20
- 34
: 11
?

Решение

а) 24, 72, 18, 45, 15.

б) 80, 16, 23, 69, 100.

в) 3, 45, 5, 60, 300.

г) 90, 51, 3, 54, 100.

д) 75, 5, 100, 66, 6.

Задание 390

Восстановите цепочку вычислений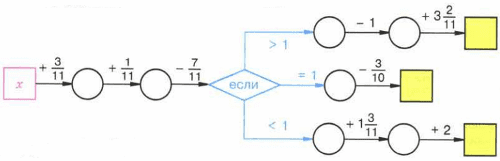

при х = 6/11 , 14/11 , 4/11 , 3/11 , 1 7/11.

Решение

6/11 → 9/11 → 10/11 → 3/11 → 1 6/11 → 3_6/11;
14/11 → 17/11 → 18/11 → 1 → 7/10;
4/11 → 7/11 → 8/11 → 1/11 → 1_4/11 → 3_4/11;
3/11 → 6/11 → 7/11 → 0 → 1_3/11 → 3_3/11;
1_7/11 → 1_10/11 → 2 → 1_4/11 → 4/11 → 3_6/11.

Задание 391

Назовите какое−либо число, расположенное на координатном луче:
а) между числами 0,1 и 0,2;
б) между 0,02 и 0,03;
в) левее 0,001, но правее 0.

Решение

а) 0,1 < 0,15 < 0,2

6) 0,02 < 0,025 < 0,3

в) 0 < 0,0005 < 0,001

Задание 392

Какую часть квадратного метра составляет:
а) 1 дм²;
б) 1 см²;
в) 10 дм²;
г) 100 см²?

Решение

а) 1 дм² = 1/100 = 0,0001 м²

б) 1 см² = 1/10000 = 0,0001 м²

в) 10 дм² = 10/100 = 0,01 м²

г) 100 см² = 100/10000 = 0,01 м²

Задание 393

Стороны треугольника 3/7 м, 4/7 м, 5/7 м. Найдите его периметр.

Решение

Р ∆ = 3/7 + 4/7 + 5/7 = 7/7 + 5/7 = 1 5/7 м.

Задание 394

Найдите число, если 3/10 его равны: 30; 15; 6.

Решение

30 : 3 * 10 = 10 * 10 = 100
15 : 3 * 10 = 5 * 10 = 50
6 : 3 * 10 = 2 * 10 = 20

Задание 395

Какая часть периода хоккейного матча сыграна, если с начала матча прошло: 5 мин; 10 мин; 15 мин; 1 мин 20 с; 20 с? (Период продолжается 20 мин.)

Решение

5 : 20 = 5/20
10 : 20 = 10/20
15 : 20 = 15/20
(60 + 20) : (20 * 60) = 80/1200
20 : (20 * 60) = 20/1200

Задание 396

Сколько Буратино заплатил за арбуз, который стоил 20 сольдо и ещё пол−арбуза?

Решение

Половина арбуза стоит 20 сольдо, поэтому арбуз стоит в 2 раза больше
20 * 2 = 40 (с.)
Ответ: 40 сольдо.

Задание 397

Сравните числа:
а) 12,567 и 125,67;
б) 7,399 и 7,4.

Решение

а) 12,567 < 125,67

б) 7,399 < 7,4

Задание 398

Между какими двумя соседними натуральными числами находится число:
а) 5,1;
б) 6,32;
в) 9,999;
г) 25,257?

Решение

а) 5 < 5,1 < 6

б) 6 < 6,32 < 7

в) 9 < 9,999 < 10

г) 25 < 25,257 < 26

Задание 399

Расставьте в порядке убывания числа:
0,915; 2,314; 0,9078; 2,316; 2,31; 10,45.

Решение

0,9078 < 0,915 < 2,31 < 2,314 < 2,316 < 10,45.

Задание 400

Расставьте в порядке возрастания величины: 8,09 км; 8165,3 м; 8154257 мм; 815376 см.

Решение

8,09 км = 8090 м
8154257 мм = 8154,257 м
815 376 см = 8153,76 м
8090 м = 8,09 км < 8153,76 м = 815376 см < 8154,257 м = 8154257 мм

Задание 401

Решите уравнение:
а) 3/5 + х = 4/5;
б) у − 2/7 = 6/7;
в) 11/25 − k = 7/25;
г) d + 2/9 = 1/9 + 7/9.

Решение

а) 3/5 + х = 4/5
x = 4/5 − 3/5
х = 1/5

б) у − 2/7 = 6/7
y = 6/7 + 2/7
у = 8/7
у = 1_1/7

в) 11/25 − k = 7/25
k = 11/25 − 7/25
k = 4/25

г) d + 2/9 = 1/9 + 7 9
d = 8/9 − 2/9
d = 6/9

Задание 402

Выразите:
а) в метрах: 17 м 8 см; 8 м 17 см; 4 см; 15 дм;
б) в тоннах: 3 т 8 ц 67 кг; 1244 кг; 710 кг.

Решение

а) 17 м 8 см = 17,08 м
8 м 17 см = 8
4 см = 0,04 м
15 дм = 1,5 м

б) 3 т 8 ц 67 = 3,867 т
1244 кг = 1,244 т
710 кг = 0,71 т

Задание 403

Решите задачу:
1) На машину погрузили 7 одинаковых мешков с мукой и 12 одинаковых мешков с крупой. Масса мешка с мукой в 2 раза больше массы мешка с крупой. Найдите массу мешка с мукой и мешка с крупой, если всего на машину погрузили 780 кг.
2) Масса индюка меньше массы овцы в 3 раза, а масса трёх таких овец больше массы пяти индюков на 60 кг. Какова масса одного индюка и какова масса одной овцы?

Решение

1) Пусть масса мешка с крупой х кг, тогда масса мешка с мукой 2х кг.
Всего на машину погрузили (7 * 2х + 12х) кг.
Составим уравнение:
7 * 2х + 12x = 780
24x = 780
х = 780 : 26
х = 30
Значит, масса мешка с крупой равна 30 кг
2 * 30 = 60 (кг) - масса мешка с мукой
Ответ: 60 кг, 30 кг.

2) Пусть у − масса индюка, тогда масса овцы 3у кг.
Разница в массе 3 овец и 5 индюков равна (3 * 3у − 5у) кг.
Составим уравнение:
3 * 3у − 5у = 60
4у = 60
у = 60 : 4
у = 15
Значит, масса индюка 15 кг
3 * 15 = 45 (кг) - масса овцы
Ответ: 15 кг, 45 кг.

Задание 404

Разгадайте чайнворд, помещённый на форзаце в конце учебника.

Решение

Гектар. 2. Разряд. 3. Длина. 4. Акр. 5.Разложение. 6. Единица. 7. Ар. 8. Радиус.
Сорок. 10. Карат. 11. Тонна. 12. Аршин. 13. Неделя. 14. Ярд. 15. Делимое.

Задание 405

Выполните сложение:
а) 395,486 + 4,58;
б) 7,6 + 908,67;
в) 0,54 + 24,1789;
г) 1,9679 + 269,0121;
д) 23,84 + 0,267;
е) 0,01237 + 0,0009876.

Решение

а) 
+ 395.486
       4.58  
   400.066

б)
+  7.6
908.67
916.27

в)
+ 0.54
 24.1789
 24.7189

г)
+  1.9679
269.0121
270.98

д)
+ 23.84
    0.267
  24.107

е)
+ 0.01237
   0.0009876
   0.0133576

Задание 406

Выполните вычитание:
а) 0,59 − 0,27;
б) 6,05 − 2,87;
в) 3,1 − 0,09;
г) 18,01 − 2,9
д) 15 − 1,12;
е) 3 − 0,07;
ж) 7,45 − 4,45;
з) 206,48 − 90,507;
и) 0,067 − 0,00389.

Решение

а)
- 0.59
  0.27
  0.32

б)
- 6.05
  2.87
  3.18

в)
- 3.1
  0.09
  3.01

г)
- 18.01
    2.9 
  15.11

д)
- 15
    1.12
  13.88

е)
- 3
  0.07
  2.93

ж)
- 7.45
  4.45
  3

з)
- 206.48
    90.507
  115.973

и)
- 0.067
  0.00389
  0.06311

Задание 407

Одна из сторон треугольника 83,6 см, вторая на 14,8 см длиннее первой, а третья на 8,6 см длиннее второй. Найдите периметр треугольника.

Решение

1) 83,6 + 14,8 = 98,4 (см) - длина второй стороны треугольника
2)  98,4 + 8,6 = 107 (см) - длина третьей стороны
3) Р∆ = 83,6 + 98,4 + 107 = 289 см = 2 м 89 см - периметр треугольника
Ответ: 2 м 89 см.

Задание 408

Трубу длиной 9,35 м разрезали на две части. Длина одной части 2,89 м. На сколько метров вторая часть длиннее первой?

Решение

1) 9,35 − 2,89 = 6,46 (м) - длина второй части 
2) 6,46 − 2,89 = 3,57 (м) -  на столько больше длина второй части трубы, чем длина первой части.
Ответ: на 3,57 м.

Задание 409

Воздушный шар состоит из оболочки, гондолы для пассажиров и газовой горелки для нагрева воздуха внутри оболочки. Масса гондолы 0,24 т, и она меньше массы оболочки на 0,32 т, но больше массы газовой горелки на 0,15 т. Какова масса воздушного шара?

Решение

 1) 0,24 + 0,32 = 0,56 (т) - масса оболочки шара
 2) 0,24 − 0,15 = 0,09 (т) - масса газовой горелки
3) 0,24 + 0,56 + 0,09 = 0,89 (т) - масса воздушного шара
Ответ: 0,89 т.

Задание 410

Автомашина в первый час прошла 48,3 км, во второй час − на 15,8 км меньше, чем в первый, а в третий час − на 24,3 км меньше, чем за первые два часа вместе. Какой путь прошла автомашина за эти три часа?

Решение

1) 48,3 − 15,8 = 32,5 (км) - прошла автомашина во второй час
2) (48,3 + 32,5) − 24,3 = 80,8 − 24,3 − 56,5 (км) - прошла автомашина в третий час
3) 48,3 + 32,5 + 56,5 = 80,8 + 56,5 = 137,3 (км) - прошла автомашина за три часа
Ответ: 137,3 км.

Задание 411

Собственная скорость теплохода 40,5 км/ч, а скорость течения 5,8 км/ч. Найдите скорость теплохода по течению и против течения.

Решение

1) 40,5 + 5,8 = 46,3 (км/ч) - скорость теплохода по течению 
2) 40,5 − 5,8 = 34,7 (км/ч) - скорость против течения 
Ответ: 46,3 км/ч, 34,7 км/ч.

Задание 412

Скорость катера по течению 23,7 км/ч. Найдите собственную скорость катера и его скорость против течения, если скорость течения 3,8 км/ч.

Решение

1) 23,7 − 3,8 = 19,9 (км/ч) - собственная скорость катера
2) 19,9 − 3,8 = 16,1 (км/ч) - скорость катера против течения

Задание 413

Выполните действия:
а) 73,12 − (5,34 + 13,12);
б) 101,3 + (84,7 + 1,11);
в) (47,28 − 34,98) + (55,02 + 34,98);
г) (46,83 + 15,77) − (6,83 − 5,77).

Решение

а) 73,12 − (5,34 + 13,12) = (73,12 − 13,12) − 5,34 = 60 − 5,34 = 54,66

б) 101,3 + (84,7 + 1,11) = (101,3 + 84,7) + 1,11 = 186 + 1,11 = 187,11

в) (47,28 − 34,98) + (55,02 + 34,98) = (47,28 + 55,02) + (34,98 − 34,98) = 102,3

г) (46,83 + 15,77) − (6,83 − 5,77) = (46,83 − 6,83) + (15,77 + 5,77) = 40 + 21,54 = 61,54

Задание 414

Разложите по разрядам числа: 41,87; 0,6098; 13,5401.

Решение

41,87 = 40 + 1 + 0,8 + 0,07
0,6098 = 0,6 + 0,009 + 0,0008
13,5401 = 10 + 3 + 0,5 + 0,04 + 0,0001

Задание 415

Запишите десятичную дробь, в которой:
а) 21 целая, 2 десятых, 8 сотых;
б) 0 целых, 0 десятых, 3 сотых, 5 тысячных.

Решение

а) 21,28

б) 0,035

Задание 416

Выразите длину отрезка AВ в метрах, дециметрах, сантиметрах и миллиметрах, если АВ = 8,906 м.

Решение

8,906 м = 89,06 дм = 890,6 см = 8906 мм.

Задание 417

Отметьте на координатном луче числа: 0,25; 0,5; 0,9; 0,37; 0,73; 1,24. За единичный отрезок примите 1 дм.

Решение

Задание 418

Решите уравнение:
а) (х − 18,2) + 3,8 = 15,6;
б) 34,2 − (17,9 − у) = 22;
в) 16,5 − (t + 3,4) = 4,9;
г) r + 16,23 − 15,8 = 7,1.

Решение

а) (х − 18,2) + 3,8 = 15,6
x − 18,2 = 15,6 − 3,8
x = 11,8 + 18,2
х = 30

б) 34,2 − (17,9 − у) = 22
17,9 − у = 34,2 − 22
у = 17,9 − 12,2
у = 5,7

в) 16,5 − (t + 3,4) = 4,9
t + 3,4 = 16,5 − 4,9
t = 11,6 − 3,4
t = 8,2

г) r + 16,23 − 15,8 = 7,1
r + 0,53 = 7,1
r = 7,1 − 0,53
r = 6,57

Задание 419

Объём прямоугольного параллелепипеда 84 см³. Этот параллелепипед разделили на две части. Найдите объём каждой части, если:
а) объём одной части в 6 раз больше объёма другой;
б) объём одной части на 40 см³ больше объёма другой.

Решение

а) Пусть х − объём меньшей части параллелепипеда, тогда 6х − объем большей части.
Сумма этих объёмов равна (х + 6х) см³.
Составим уравнение:
х + 6х = 84
х = 84 : 7
х = 12
Значит, 12 см³ − объём меньшей части
6 * 12 = 72 (см³) - объем большей части
Ответ: 12 см³ , 72 см³.

б) Пусть у − объём одной части, тогда (у + 40) − объём другой.
Сумма этих объёмов равна (у + у + 40) см³.
Составим уравнение:
у + (у + 40) = 84
2у = 84 − 40 = 44
у = 44 : 2
у = 22
Значит, 22 см³ − объём одной части
22 + 40 = 62 (см³) - объем другой части
Ответ: 22 см³ , 62 см³.