Параграф 8. Инструменты для вычислений и измерений

Пункт 39. Микрокалькулятор

Задание 689

Прочитайте показание на индикаторе (рис. 157):

Решение

Две тысячи пятьсот четыре целых одна тысяча семьсот тридцать четыре десятитысячных.

Задание 690

Введите в микрокалькулятор числа:
20 000; 45 897; 3,9045; 0,000761.

После введения каждого числа не забывайте сбрасывать предыдущее число.

Задание 691

Выполните с помощью микрокалькулятора действия:
а)
39,614 + 89,213;
560,98 + 1039,71;
0,0876 + 0,0876;
0,0876 + 0,91469;
24714395 + 39623008;
б)
98,542 − 67,413;
714,932 − 521,081;
0,09854 − 0,05421;
76539086 − 22612007;
в)
24,15 * 39,52;
1,987 * 2,608;
0,5637 * 0,451;
0,0567 * 2,371;
г)
18,324169 : 3,427;
621,83538 : 24,501;
673074,72 : 941,1.

Решение

а) 39,614 + 89,213 = 128,827
560,98 + 1039,71 = 1600,69
0,0876 + 0,0876 = 0,1752
0,0876 + 0,91469 = 1,00229
24174395 + 39623008 = 63797403

б) 98,542 − 67,413 = 31,129
714,932 − 521,081 = 193,851
0,09854 − 0,05421 = 0,04433
76539086 − 22612007 = 53927079

в) 24,15 * 39,52 = 954,408
1,987 * 2,608 = 5,182096
0,5637 * 0,451 = 0,2542287
0,0567 * 2,371 = 0,1333257

г) 18,324169 : 3,427 = 5,347
621,83538 : 24,501 = 25,38
673074,72 : 941,1 = 715,2

Задание 692

Выполните письменно, а потом проверьте ответ с помощью микрокалькулятора:
а) 45,614 + 20,542;
б) 510,78 − 248,81;
в) 76,2 * 2,45;
г) 821,1 : 34,5.

Решение

а) + 45.614
       20.542
       66.156

б) - 510.78
      248.81
      261.97

в) × 76,2
       2,45
      3810
    3048
  1524     
 186,690

г) 821,1 : 34,5 = 8211 : 345
_8211 |345
  690   |23,8
_1311
  1035
  _2760
    2760
          0

Задание 693

С помощью микрокалькулятора найдите значение выражения:
а) 412,89 + 306,24 − 678,59;
б) 8,508 + 9,439 − 2,524;
в) 0,769 * 5,142 * 3,71;
г) 9,725 * 1,06 : 3,89;
д) 24,78 * 51,8 + 248,713;
е) 871,017 : 5,05 − 11,376;
ж) (280,65 + 317,25) * 4,24;
з) (953,54 − 396,41): 75,8 * 4,12.

Решение

а) 412,89 + 306,24 − 678,59 = 719,13 − 678,59 = 40,54

б) 8,508 + 9,439 − 2,524 = 17,947 − 2,524 = 15,423

в) 0,769 * 5,142 * 3,71 = 3,954198 * 3,71 = 14,67007458

г) 9,725 * 1,06 : 3,89 = 10,3085 : 3,89 = 2,65

д) 24,78 * 51,8 + 248,713 = 1283,604 + 248,713 = 1532,317

e) 871,017 : 5,05 − 11,376 = 161,786 − 11,376 = 150,410

ж) (280,65 + 317,25) * 4,24 = 597,9 * 4,24 = 2535,096

з) (953,54 − 396,41) : 75,8 * 4,12 = 557,13 : 75,8 * 4,12 = 7,35 * 4,12 = 30,282

Задание 694

Вычислите устно:
а) 7 + 0,2
: 9
* 3
+ 0,6
?
б) 10,9 - 1
: 3
+ 2,7
: 4
?
в) 6 - 2,4
: 6
+ 0,4
: 2
?
г) 40 * 0,4
: 10
+ 0,5
: 7
?

Решение

а) 7,9, 0,8, 2,4, 3.

б) 9,9, 3,3, 6, 1,5.

в) 3,6, 0,6, 1, 0,5.

г) 16, 1,6, 2,1, 0,3.

Задание 695

Выполните деление:
а) 2/5;
6) 1/20;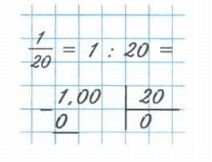

в) 1/25;
г) 1/4;
д) 18/10;
е) 1 : 2 = 0,5;
ж) 3 : 15 = 0,2;
з) 5 : 0,2 = 25;
и) 1 : 0,01 = 100;
к) 0,8 : 0,04 = 20;
л) 1 : 0,25 = 4;
м) 1 : 1,25 = 0,8.

Решение

а)
_2 |5   
  0 |0,4
_20
  20
    0

б)
_1 |20   
  0 |0.05
_10
    0
_100
  100
      0

в)
_1 |25    
  0 |0.04
_10
    0
_100
  100
      0

г)
_1 |4     
  0 |0.25
_10
    8
  _20
    20
      0

д)
_18 |10  
  10 |1.8
  _80
    80
      0

е)
_1 |2   
  0 |0,5
_10
  10
    0

ж) 
_3 |15
  0 |0,2
_30
  30
    2

з) 5 : 0,2 = 50 : 2 =25

и) 1 : 0,01 = 100 : 1 = 100

к) 0,8 : 0,04 = 80 : 4 = 20

л) 1 : 0,25 = 100 : 25 = 4

м) 1 : 1,25 = 100 : 125 = 0,8
_100 |125
      0 |0,8
_1000
  1000
        0

Задание 696

Найдите:
а) 0,01 числа 50;
б) 0,07 числа 300;
в) 0,6 числа 40;
г) 0,25 числа 36.

Решение

а) 50 * 0,01 = 0,5

б) 300 * 0,07 = 21

в) 40 * 0,6 = 24

г) 36 * 0,25 = 9

Задание 697

Каким одним действием можно:
а) уменьшить число в 10 раз; в 100 раз?
б) увеличить число в 100 раз; в 1000 раз?
Приведите примеры.

Решение

а) при делении на 10, 100

б) при умножении на 100, 1000

Задание 698

На первом участке пути автомобиль двигался 3 ч со скоростью 40 км/ч, а на втором − 1 ч со скоростью 60 км/ч. Какова средняя скорость автомобиля на всём пути?

Решение

Средняя скорость движения автомобиля равна (40 * 3 + 60 * 1) : (3 + 1) = (120 + 60) : 4 = 180 : 4 = 45 км/ч.

Задание 699

Составьте задачу по числовому выражению:
а) (2,6 + 2,8) : 2;
б) (3,8 + 3,7 + 3,6) : 3.

Решение

а) Турист до обеда шел со скоростью 2,6 км/ч, а после обеда 2,8 км/ч. С какой средней скоростью прошел маршрут турист?

(2,6 + 2,8) : 2 = 5,4 : 2 = 2,7 (км/ч) - средняя скорость туриста.
Ответ: 2,7 км/ч.

б) Три грибника собирали грибы. Первый собрал 3,8 кг, второй 3,7 кг, а третий 3,6 кг. Сколько грибов будет у каждого грибника, если они решили что разделят все собранные грибы поровну?

(3,8 + 3,7 + 3,6) : 3 = 11,1 : 3 = 3,7 (кг) - грибов будет у каждого грибника.
Ответ: 3,7 кг.

Задание 700

Найдите четвёртое число в последовательности:
а) 2; 4; 16; ?;
б) 3; 9; 81;?;
в) 6; 3; 1,5; ?;
г) 0,1; 0,5; 2,5; ?.

Решение

а) Каждое следующее число равно квадрату предыдущего: 2; 4; 16; 256.

б) Каждое следующее число равно квадрату предыдущего: 3; 9; 81; 6561.

в) Каждое следующее число равно половине предыдущего: 6; 3; 1,5; 0,75.

г) Каждое следующее число в 5 раз больше предыдущего: 0,1; 0,5; 2,5; 12,5.

Задание 701

Найдите среднее арифметическое чисел:
а) 81,242; 65,312; 412,54; 94,376;
б) 71,3; 25,7; 39,8; 12,9; 56,4.

Решение

а) (81,242 + 65,312 + 412,54 + 94,376) : 4 = 653,47 : 4 = 163,3675

б) (71,3 + 25,7 + 39,8 + 12,9 + 56,4) : 5 = 206,1 : 5 = 41,22

Задание 702

Теплоход прошёл 70 км по реке за 2 ч и 90 км по озеру за 3 ч. С какой средней скоростью прошёл теплоход весь путь?

Решение

Теплоход прошёл весь путь со средней скоростью (70 + 90) : (2 + 3) = 160 : 5 = 32 км/ч.

Задание 703

Овощевод−опытник снял с одного куста помидоров 12 плодов по 250 г, 10 плодов по 330 г и 8 плодов по 210 г. Найдите среднюю массу одного помидора.

Решение

(250 * 12 + 330 * 10 + 210 * 8) : (12 + 10 + 8) = (3000 + 3300 + 1680) : 30 = 7980 : 30 = 266 (г) - средняя масса одного помидора
Ответ: 266 г.

Задание 704

Среднее арифметическое четырёх чисел 6,7. Первое равно 2, второе в 1,2 раза больше первого, а третье меньше четвёртого в 1,5 раза. Найдите третье и четвёртое числа.

Решение

Пусть третье число равно x.
Составим уравнение:
(2 + (1,2 * 2) + 1,5x + х) : 4 = 6,7
4,4 + 2,5х = 6,7 * 4
х = (26,8 − 4,4) : 2,5
х = 8,96 − третье число,
1,5 * 8,96 = 13,44 − четвёртое число.
Ответ: 8,96 и 13,44.

Задание 705

Пассажирский поезд прошёл путь от одной станции до другой со средней скоростью 67 км/ч. Вначале он шёл 4 ч со скоростью 59,5 км/ч, а затем увеличил скорость и прибыл на вторую станцию через 3 ч. Найдите скорость поезда на втором участке пути.

Решение

Пусть х − скорость поезда на втором участке пути,
тогда средняя скорость поезда на всем пути равна
(59,5 * 4 + х * 3) : (4 + 3) км/ч.
Составим уравнение:
(59,5 * 4 + х * 3) : (4 + 3) 
                      469
238 + 3х = 67 * 7 
х = (469 − 238) : 3
х = 231 : 3
х = 77
Значит,  скорость поезда на втором участке пути 77 км/ч.
Ответ: 77 км/ч.

Задание 706

Серёжа стал на велосипеде догонять Наташу, идущую пешком, когда между ними было 600 м, и догнал её через 4 мин. Найдите скорость, с которой шла Наташа, если её скорость в 4 раза меньше скорости Серёжи.

Решение

Пусть х м/мин − скорость Наташи,
тогда скорость Сережи 4х м/мин.
Составим уравнение:
600 : (4х − х) = 4
3х = 600 : 4 
х = 150 : 3
х = 50
Значит, скорость Наташи 50 м/мин.
Ответ: 50 м/мин.

Задание 707

С двух грядок, общая площадь которых 40,5 м², получили 137,7 кг моркови. Сколько килограммов моркови собрали с каждой грядки, если площадь одной из них на 4,5 м² меньше, чем площадь другой, а урожайность одинакова?

Решение

Пусть площадь одной грядки − х м²,
тогда (х + 4,5) м² − площадь другой грядки.
Составим уравнение:
х + х + 4,5 = 40,5
2х = 40,5 − 4,5 − 36
х = 36 : 2
х = 18
Значит, 18 м² − площадь одной грядки,
18х + 4,5 = 22,5 (м²) − площадь другой грядки.
137,7 : 40,5 = 3,4 (кг/м²) - урожайность моркови
18 * 3,4 = 61,2 (кг) - моркови получили с первой грядки
22,5 * 3,4 = 76,5 (кг) - моркови получили со второй грядки
Ответ: 61,2 кг,  76,5 кг.

Задание 708

Запишите в виде равенства предложение:
а) 5n на 8,11 больше n;
б) утроенное а на 5,18 больше а;
в) разность m и 9,11 в 4 раза меньше их суммы.

Решение

а) 5n − n = 8,11

б) 3а − а = 5,18

в) (m + 9,11) : (m − 9,11) = 4

Задание 709

С помощью микрокалькулятора вычислите значение выражения:
а) 78,627 + 3,081;
б) 735,24 − 261,87;
в) 41,65 * 85,38;
г) 62,14 : 9,241;
д) 508,3 + 891,4 : 35,4;
е) 92,5 * 11,6 − 429,15.

Решение

а) 78,627 + 3,081 = 81,708

б) 735,24 − 261,87 = 473,37

в) 41,65 − 85,38 = 3556,077

г) 62,14 : 9,241 = 6,7243804

д) 508,3 + 891,4 : 35,4 = 508,3 + 25,181 = 533,481

e) 92,5 * 11,6 − 429,15 = 1073 − 429,15 = 643,85

Задание 710

Найдите с помощью микрокалькулятора объём прямоугольного параллелепипеда по формуле V = abc, если:
a = 2,81 дм; b = 1,76 дм; с = 4,9 дм; ответ округлите до сотых.

Решение

При a = 2,81 дм, b = 1,76 дм и с = 4,9 дм:
V = a b с = 2,81 * 1,76 * 4,9 = 24,23344 (дм³)
24,23344 дм³ ≈ 24,23 дм³.
Ответ: 24,23 дм³.

Задание 711

Два поезда одновременно вышли навстречу друг другу из двух городов, расстояние между которыми 495 км. Через 3 ч они встретились. Какова скорость каждого поезда, если известно, что скорость одного из них на 5 км/ч больше скорости другого?

Решение

Пусть х км/ч скорость одного поезда,
тогда (х + 5) км/ч скорость другого поезда.
Скорость сближения поездов равна (х + х + 5) км/ч,
поезда встретились через 495 : (х + х + 5) ч.
Составим уравнение:
495 : (х + х + 5) = 3
2х + 5 = 495 : 3
х = (165 − 5) : 2
х = 80
Значит, 80 км/ч − скорость одного поезда равна
80 + 5 = 85 (км/ч) - скорость другого поезда
Ответ: 80 км/ч и 85 км/ч.

Задание 712

Два велосипедиста одновременно выехали навстречу друг другу из двух посёлков, расстояние между которыми 76 км. Через 2 ч они встретились. Какова скорость каждого велосипедиста, если известно, что скорость одного из них в 1,5 раза больше скорости другого?

Решение

Пусть х − скорость одного велосипедиста,
тогда 1,5x − скорость другого велосипедиста.
Велосипедисты встретились через 76 : (x + 1,5x) ч.
Составим уравнение:
76 : (у + 1,5y) = 2
2,5у = 76 : 2
у = 38 : 2,5
у = 15,2
Значит, 15,2 км/ч − скорость одного велосипедиста
1,5 * 15,2 = 22,8 (км/ч) - скорость другого велосипедиста
Ответ: 15,2 км/ч, 22,8 км/ч.

Задание 713

Выполните действия и проверьте ответ с помощью микрокалькулятора:
((4 : 0,128 + 14 628,25) : 1,011 * 0,00008 + 6,84) : 12,5.

Решение

((4 : 0,128 + 14628,25) : 1,011 * 0,00008 + 6,84) : 12,5 = (14500 − 0,00008 + 6,84) : 12,5 = 8 : 12,5 = 0,64.

 

Пункт 40. Проценты

Задание 714

Запишите в виде десятичной дроби:
1%; 6%; 45%; 123%; 2,5%; 0,4%.

Решение

1% = 1 * 0,01 = 0,01
6% = 6 * 0,01 = 0,06
45% = 45 * 0,01 = 0,45
123% = 123 * 0,01 = 1,23
2,5% = 2,5 * 0,01 = 0,025
0,4% = 0,4 * 0,01 = 0,004

Задание 715

Запишите в процентах десятичные дроби: 0,87; 0,07; 1,45; 0,035; 2,672; 0,907.

Решение

0,87 = 0,87 * 100% = 87%
0,07 = 0,07 * 100% = 7%
1,45 * 100% = 145%
0,035 * 100% = 3,5%
2,672 = 2,672 * 100% = 267,2%
0,907 = 0,907 * 100% = 90,7%

Задание 716

Запишите обыкновенные дроби 1/2 ; 1/4 ; 3/4 ; 2/5 ; 17/50 в виде десятичных, а потом в виде процентов.

Решение

1/2 = 0,5 = 0,5 * 100% = 50%
1/4 = 0,25 = 0,25 * 100% = 25%
3/4 = 0,75 = 0,75 * 100% = 75%
2/5 = 0,4 = 0,4 * 100% = 40%
17/50 = 0,34 = 0,34 * 100% = 34%

Задание 717

Заполните таблицу:

Решение

Задание 718

В школьной библиотеке 7000 книг. Маша прочитала одну сотую всех этих книг. Сколько библиотечных книг прочитала Маша?
Серёжа прочитал 1% всех книг школьной библиотеки. Сравните число библиотечных книг, прочитанных Машей и Серёжей.

Решение

1/100 это и есть 1%, значит Маша и Миша прочитали одинаковое количество книг.
Проверим:
1) 7000 * 0,01 = 70 (к.) - прочитала Маша
2) 7000 : 100 * 1 = 70 (к.) - прочитал Серёжа
Ответ: по 70 книг прочитали Маша, Серёжа.

Задание 719

В палатку завезли 850 кг огурцов. Первый покупатель взял для соления 1% всех огурцов, а второй − 3% всех огурцов. Сколько килограммов огурцов купил каждый из них?

Решение

850 - 100%
    ? - 1%
1) 850 : 100 * 1 = 8,5 (кг) - огурцов купил первый покупатель
850 - 100%
    ? - 3%
2) 850 : 100 * 3 = 8,5 * 3 = 25,5 (кг) - огурцов купил второй покупатель
Ответ: 8,5 кг и 25,5 кг.

Именно таким способом разобрано решение задач на проценты в учебнике Виленкина. Но можно их решить другим способом - переводя проценты в десятичную дробь. Ваш учитель может потребовать от вас решение обеими способами, поэтому, на примере данной задачи раберем и второй. 

    1 % = 0,01
1) 850 * 0,01 = 8,5 (кг) - огурцов купил первый покупатель
    3% = 0,03
2) 850 * 0,03 = 8,5 * 3 = 25,5 (кг) - огурцов купил второй покупатель
Ответ: 8,5 кг и 25,5 кг.

Напишите нам в комментариях, каким способом решаете задачи на проценты вы: находя сначала 1% делением на 100 или через перевод процентов в дроби?

Задание 720

На поле, площадь которого 620 га, работали хлопкоуборочные машины. За сутки они убрали 15% всего поля. Сколько гектаров хлопка убрали за сутки?

Решение

620 га - 100%
       ? - 15%
620 : 100 * 15 = 93 (га) - хлопка убрали за сутки
Ответ: 93 га.

Задание 721

Бригаде поручили отремонтировать участок дороги длиной 760 м. Сколько метров дороги бригада отремонтирует, когда выполнит: 30% задания; 50% задания; 10% задания?

Решение

1) 760 : 100 = 7,6 (м) - 1%
2) 7,6 * 30 = 228 (м) - дороги отремонтируют, когда выполнят 30% задания
3) 7,6 * 50 = 380 (м) - дороги отремонтируют, когда выполнят 50% задания
4) 7,6 * 10 = 76  (м) - дороги отремонтируют, когда выполнят 10% задания
Ответ: 228 м, 380 м, 76 м. 

Задание 722

Предприятие изготовило за квартал 500 насосов, из которых 60% имели высшую категорию качества. Сколько насосов высшей категории качества изготовило предприятие?

Решение

500 : 100 * 60 = 5 • 60 = 300 (н.) - высшей категории качества изготовило предприятие.
Ответ: 300 насосов.

Задание 723

В плодовом саду собирали яблоки. За день было собрано 4840 кг. 25% собранных яблок отправили в магазин, а остальные − на склад. Сколько килограммов яблок отправили на склад?

Решение

1) 100% − 25% = 75% собранных яблок отправили на склад,
2) 4840 : 100 * 75 = 48,4 * 75 = 3630 (кг) - яблок отправили на склад
Ответ: 3630 кг.

Задание 724

Себестоимость изготовления одной детали равна 650 р. Внедрение новой технологии позволило снизить себестоимость детали на 2%. Какова стала себестоимость такой детали?

Решение

1) 100% − 2% = 98% от прежней себестоимости составила новая себестоимость детали,
2) 650 : 100 * 98 = 6,5 * 98 = 637 (р.) - стала себестоимость детали
Ответ: 637 рублей.

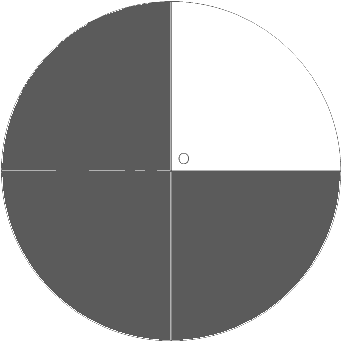
Задание 725

Поле на рисунке 158 разбито на 100 долей. Закрашенная на рисунке часть засеяна горохом. Найдите площадь всего поля, если горохом засеяно 24,8 га.

Решение

Горохом засеяно 8% всего поля, что соответствует 24,8 га.
24,8 : 8 * 100 = 3,1 * 100 = 310 (га) - площадь всего поля
Ответ: 310 га.

Задание 726

Сколько человек было в кино, если 1% всех зрителей составляет 7 человек?

Решение

7 : 0,01 = 7 * 100 = 700 (ч.) - было в кино
Ответ: 700 человек.

Задание 727

Мотоциклист за день проехал некоторое расстояние. 1% пути он ехал по просёлочной дороге, что составило 3,2 км. Какое расстояние проехал мотоциклист за день?

Решение

3,2 : 0,01 = 3,2 * 100 = 320 (км) - проехал мотоциклист за день
Ответ: 320 км.

Задание 728

Двор разбит на 100 равных частей. Часть площади двора, закрашенная на рисунке 159, отведена под стоянку машин. Найдите площадь двора, если стоянка занимает 146,4 м².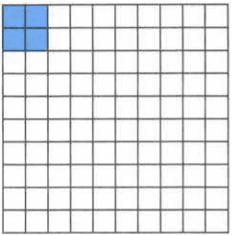

Решение

Стоянка машин занимает 4% от площади двора, что соответствует 146,4 м².
146,4 : 4 * 100 = 36,6 * 100 = 3660 (м²) - площадь двора
Ответ: 3660 м².

Задание 729

Ученик прочитал 138 страниц, что составляет 23% числа всех страниц в книге. Сколько страниц в книге?

Решение

138 : 23 * 100 = 6 * 100 = 600 (с.) - в книге
Ответ: 600 страниц.

Задание 730

Масса медвежонка составляет 15% массы белого медведя. Найдите массу белого медведя, если масса медвежонка 120 кг.

Решение

120 : 15 * 100 = 8 * 100 = 800 (кг) - масса белого медведя
Ответ: 800 кг.

Задание 731

Сливочное мороженое содержит 14% сахара. На приготовление мороженого израсходовали 35 кг сахара. Сколько сделали порций мороженого, если в каждой порции 100 г?

Решение

1) 35 : 14 * 100 = 2,5 * 100 = 250 кг - мороженого получили из 35 кг сахара 
250 кг = 250000 (г)
2) 250000 : 100 = 2500 (п.) - мороженого получили
Ответ: 2500 порций.

Задание 732

Применяя интенсивную технологию, бригада изготовила сверх плана 250 деталей, перевыполнив тем самым план на 5% . Сколько деталей изготовила бригада?

Решение

1) 250 : 5 * 100 = 50 * 100 = 5000 (д.) - должна была изготовить бригада по плану
2) 5000 + 250 = 5250 (д.) - всего изготовила бригада
Ответ: 5250 деталей.

Задание 733

В школе 700 учащихся. Среди них 357 мальчиков. Сколько процентов учащихся этой школы составляют мальчики?

Решение

357 : 700 = 0,51 часть всех учащихся составляют мальчики
0,51 = 51%
Ответ: 51%.

Задание 734

Фрекен Бок испекла 80 пирожков, и Карлсон тут же съел 10 пирожков. Сколько процентов всех пирожков съел Карлсон?

Решение

10 : 80 = 0,125 часть всех пирожков съел Карлсон
0,125 = 12,5%
Ответ: 12,5%.

Задание 735

В механическом цехе установлено 350 станков, из которых 35 находятся в ремонте. Сколько процентов станков находятся в действующем состоянии?

Решение

1) 350 − 35 = 315 (с.) - находится в действующем состоянии
2) 315 : 350 = 0,9 всех станков находится в действующем состоянии
0,9 = 90%
Ответ: 90%.

Задание 736

При плане 35 деталей в день рабочий сделал 42 детали. На сколько процентов он выполнил норму? На сколько процентов он перевыполнил норму?

Решение

1) 42 : 35 = 1,2 часть всего плана выполнил рабочий
    1,2 = 120%
2) 120% − 100% = 20% - на столько рабочий перевыполнил норму
Ответ: на 20%.

Задание 737

Сколько процентов соли содержит раствор, приготовленный из 35 г соли и 165 г воды?

Решение

1) 35 + 165 = 200 (г) - масса раствора
2) 35 : 200 = 0,175 всего раствора занимает соль
0,175 = 17,5%
Ответ: 17,5%.

Задание 738

В 4−А классе 40 учеников. С задачей справились 32 ученика. В 4−Б классе 35 учеников, а с задачей справились 28 учеников. Какой класс лучше справился с задачей?

Решение

1) 32 : 40 = 0,8 от всех учеников справились  с задачей в 4А
     0,8 = 80%
2) 28 : 35 = 0,8 от всех учеников справились с задачей в 4Б
    0,8 = 80%
Ответ: оба класса одинаково хорошо справились с задачей.

Задание 739

Найдите 0,3 числа:
а) 150;
б) 600;
в) 100;
г) 5.

Решение

а) 150 * 0,3 = 45

б) 600 * 0,3 = 180

в) 100 * 0,3 = 30

г) 5 * 0,3 = 1,5

Задание 740

Вычислите устно:
а) 1,45 + 0,15
* 4
+ 0,8
: 0,8
?
б) 9,8 - 5,9
: 1,3
+ 1,8
* 2
?
в) 30 * 0,01
+ 2,4
: 0,9
: 0,1
?
г) 0,2 * 50
: 2,5
+ 0,8
* 5
?
д) 8 * 0,2
: 0,8
- 0,6
* 5
?

Решение

а) 1,6, 6,4, 7,2, 9.

б) 3,9, 3, 4,8, 9,6.

в) 0,3, 2,7, 3, 30.

г) 10, 4, 4,8, 24.

д) 1,6, 2, 1,4, 7.

Задание 741

Представьте в виде десятичной дроби 3 1/2 ; 1 1/4 ; 2 1/5 ; 7 1/20 ; 9 1/25.

Решение

3 1/2 = 3,5
1 1/4 = 1,25
2 1/5 = 2,2
7 1/20 = 7,05
9 1/25 = 9,04

Задание 742

Восстановите цепочки вычислений и попробуйте объяснить, почему они приводят к одному ответу: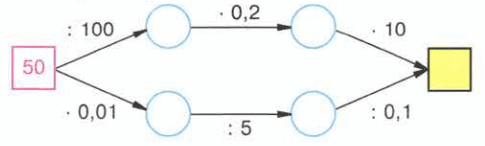

Решение

50 → 0,5 → 0,1 → 1
50 → 0,5 → 0,1 → 1
Деление производится на обратное умножению число.

Задание 743

Собственная скорость катера 18 км/ч. Отметьте её на координатном луче. Вычислите и отметьте на этом луче скорости катера против течения и по течению, если скорость течения 1,5 км/ч. Используя чертёж, подумайте:
а) как найти собственную скорость катера, если известны его скорости по течению и против течения;
б) как найти скорость катера против течения, если известны скорость течения и скорость катера по течению;
в) на сколько скорость катера по течению больше его скорости против течения?

Решение

а) При известных скоростях катера по течению и против собственная скорость катера равна среднему арифметическому этих скоростей.

б) При известной скорости катера по течению и скорости течения скорость против течения равна разности скорости по течению и удвоенной скорости течения.

в) Скорость катера по течению больше скорости против течения на величину удвоенной скорости течения.

Задание 744

Попробуйте представить правило нахождения среднего арифметического нескольких чисел и средней скорости в виде последовательности команд по схемам:...

Решение

Чтобы найти среднее арифметическое нескольких чисел, нужно:
1) найти сумму этих чисел;
2) найти число этих чисел;
3) разделить сумму чисел на их число.
Чтобы найти среднюю скорость, нужно:
1) найти пройденный путь;
2) найти общее время движения;
3) разделить пройденный путь на время движения.

Задание 745

Найдите значение выражения:
а) 2,0928 + 47,9072 : (7 − 0,195);
б) 100,5876 − 88,5856 : (6,0811 + 8,4889);
в) 687,8 + (88,0802 − 85,3712) : 0,045.
Проверьте ответ с помощью микрокалькулятора.

Решение

а) 2,0928 + 47,9072 : (7 − 0,195) = 2,0928 + 47,9072 : 6,805 = 2,0928 + 7,04 = 9,1328

б) 100,5876 − 88,5856 : (6,0811 + 8,4889) = 100,5876 − 88,5856 : 14,57 = 100,5867 − 6,08 = 94,5076

в) 687,8 + (88,0802 − 85,3712) : 0,045 = 687,8 + 2,709 : 0,045 = 687,8 + 60,2 = 748

Задание 746

Автобус шёл 3 ч по шоссе, 1,5 ч по грунтовой дороге и 0,5 ч по просёлочной дороге. Известно, что скорость автобуса по грунтовой дороге была в 2 раза больше скорости по просёлочной дороге, а скорость по шоссе в 3,5 раза больше скорости по просёлочной дороге. Найдите скорость движения автобуса по просёлочной дороге, если средняя скорость автобуса на всём пути 33,6 км/ч.

Решение

Пусть скорость автобуса по проселочной дороге − х км/ч ,
тогда его скорость по грунтовой дороге − 2х км/ч,
а скорость автобуса по шоссе − 3,5х км/ч.
Средняя скорость автобуса на всем маршруте равна:
(3,5х − 3 + 2x1,5 + х − 0,5) : (3 + 1,5 + 0,5) км/ч.
Составим уравнение:
(3,5х − 3 + 2x1,5 + х − 0,5) : (3 + 1,5 + 0,5) = 33,6
10,5х + 3х + 0,5х = 33,6 − 5 
14х = 168
х = 168 : 14
х = 12
Значит, скорость движения автобуса по просёлочной дороге 12 км/ч.
Ответ: 12 км/ч.

Задание 747

Марина сварила варенье, истратив 5/8 имевшегося у неё сахара. Сколько сахара осталось у Марины, если на варенье она израсходовала 0,8 кг сахара?

Решение

1) 0,8 : 5 * 8 = 0,16 * 8 = 1,28 (кг) - сахара было у Марины всего
2) 1,28 − 0,8 = 0,48 (кг) - сахараосталось
Ответ: 0,48 кг.

Задание 748

В куске было 112,2 м материи. В первый раз отрезали 3/17 куска, а во второй раз 7/17 куска. Сколько метров материи было отрезано за оба раза?

Решение

1) 3/17 + 7/17 = 10/17 куска материи было отрезано за оба раза
2) 112,2 : 17 * 10 = 6,6 * 10 = 66 (м) - материи было отрезано за оба раза
Ответ: 66 м.

Задание 749

Выполните действия:
1) (3,1 * 5,3 − 14,39) : 1,7 + 0,8;
2) (21,98 − 4,2 * 4,6) : 1,9 + 0,6.

Решение

1) (3,1 * 5,3 − 14,39) : 1,7 + 0,8 = (16,43 − 14,39) : 1,7 + 0,8 = 2,04 : 1,7 + 0,8 = 1,2 + 0,8 = 2

2) (21,98 − 4,2 * 4,6) : 1,9 + 0,6 = (21,98 − 19,32) : 1,9 + 0,6 = 2,66 : 1,9 + 0,6 = 1,4 + 0,6 = 2

Задание 750

Решите задачу:
1) Первое число в 2,4 раза больше третьего, а второе число на 0,6 больше третьего числа. Найдите эти три числа, если их среднее арифметическое равно 2,4.
2) Второе число на 0,8 больше первого, а третье число в 3,2 раза больше первого. Найдите эти три числа, если их среднее арифметическое равно 4,6.

Решение

1) Пусть у − третье число равно,
тогда первое число − 2,4y,
а второе: у + 0,6.
Среднее арифметическое этих чисел равно (2,4y + у + 0,6 + у) : 3.
Составим уравнение:
(2,4y + у + 0,6 + у) : 3 = 2,4
4,4y + 0,6 = 2,4 * 3
y = (7,2 − 0,6) : 4,4y
у = 1,5 − третье число,
2,4 − 1,5 = 3,6 − первое число,
1,5 + 0,6 = 2,1 − второе число.
Ответ: 3,6; 2,1; 1,5.

2) Пусть х − первое число, тогда второе число − х + 0,8, третье − 3,2х.
Среднее арифметическое этих чисел равно (х + x + 0,8 + 3,2x) : 3.
Составим уравнение:
(х + х + 0,8 + 3,2Х) : 3 = 4,6
5,2х + 0,8 = 4,6 * 3
x = (13,8 − 0,8) : 5,2
x = 2,5 − первое число,
2,5 + 0,8 = 3,3 − второе число,
3,2 * 2,5 = 8 − третье число.
Ответ: 2,5; 3,3; 8.

Задание 751

Запишите в виде процентов десятичные дроби 6,51; 2,3; 0,095.

Решение

6,51 = 6,51 * 100% = 651%
2,3 = 2,3 * 100% = 230%
0,095 = 0,095 * 100% = 9,5%

Задание 752

Запишите в виде десятичной дроби
42%; 8%; 7,25%; 568%.

Решение

42% = 42 * 0,01 = 0,42
8% = 8 * 0,01 = 0,08
7,25% = 7,25 * 0,01 = 0,0725
568% = 568 * 0,01 = 5,68

Задание 753

Слесарь и его ученик изготовили 1200 деталей. Ученик сделал 30%. всех деталей. Сколько деталей сделал ученик?

Решение

30% = 0,3
1200 * 0,3 = 360 (д.) - сделал ученик
Ответ: 360 деталей

Задание 754

На водопой пригнали 220 лошадей и жеребят. Жеребята составляли 15% всего табуна. Сколько жеребят было в табуне?

Решение

15% = 0,15
220 * 0,15 = 33 (ж.) - было в табуне
Ответ: 33 жеребёнка.

Задание 755

Геологи проделали путь длиной 2450 км. 10% пути они пролетели на самолёте, 60% пути проплыли в лодках, а остальную часть прошли пешком. Сколько километров геологи прошли пешком?

Решение

1) 100% − (10% + 60%) = 100% − 70% = 30% пути прошли геологи пешком
30% = 0,3
2) 2450 * 0,3 = 735 (км) - прошли геологи пешком
Ответ: 735 км.

Задание 756

Из молока получается 10% творога. Сколько творога получится из 32,8 кг молока? Из 58,7 кг молока?

Решение

10% = 0,1
В 32,8 кг молока 10% творога
1) 32,8 * 0,1 = 3,28 (кг) - творога получится из 32,8 кг молока
В 58,7 кг молока 10% творога
2) 58,7 * 0,01 * 10 = 0,587 * 10 = 5,87 (кг) - творога получится из 58,7 кг молока
Ответ: 3,28 кг, 5,87 кг.

Задание 757

Площадь одной комнаты 12 м², и она составляет 25% площади всей квартиры. Найдите площадь всей квартиры.

Решение

25% составляет 12 м²
25% = 0,25
12 : 0,25 = 48 (м²) - площадь всей квартиры
Ответ: 48 м².

Задание 758

Автотурист проехал в первый день 120 км, что составляет 15% всего намеченного пути. Какой длины намеченный путь?

Решение

15% составляет 120 км
15% = 0,15
120 : 0,15 = 800 (км) - длина намеченного пути 
Ответ: 800 км.

Задание 759

Засеяли 24% поля. Осталось засеять 45,6 га этого поля. Найдите площадь всего поля.

Решение

1) 100% − 24% = 76% поля осталось засеять
    76% составляет 45,6 га.
    76% = 0,76
2) 45,6 : 0,76 = 60 (га)  - площадь всего поля

Задание 760

Из пшеницы получается 80% муки. Сколько смололи пшеницы, если получили 2,4 т муки? Сколько муки получится из 2,5 т пшеницы?

Решение

80% = 0,8
2,4 т составляют 80%
1)  2,4 : 0,8 = 3 (т) - пшеницы смололи при получении 2,4 т муки
80% от 2,5 т
2) 2,5 * 0,8 = 2  (т) - муки получится из 2,5 т пшеницы
Ответ: 3 т, 2 т.

Задание 761

Масса сушёных яблок составляет 16% массы свежих яблок. Сколько надо взять свежих яблок, чтобы получить 4 т сушёных? Сколько сушёных яблок получится из 4,5 т свежих яблок?

Решение

16% = 0,16
4 т  составляют 16%
1)  4 : 0,16 = 25 (т) -  свежих яблок надо взять для получения 4 т сушёных яблок
16% от 4,5 т 
2) 4,5 * 0,16 = 0,72 (т) сушеных яблок получится из 4,5 т свежих яблок

Задание 762

Из 200 арбузов 16 оказались незрелыми. Сколько процентов всех арбузов составили незрелые арбузы?

Решение

16 : 200 = 0,08 всех арбузов оказались незрелыми
0,08 = 8%
Ответ: 8%.

Задание 763

В классе 17 мальчиков, а девочек на 6 больше. Сколько процентов класса составляют девочки и сколько процентов класса составляют мальчики?

Решение

1) 17 + 6 = 23 (уч.) - девочек в классе
2) 17 + 23 = 40 (уч.) - всего в классе
3)  23/40 = 0,575 от всех учеников в классе составляют девочки
     0,575 = 57,5%
4) 100% − 57,5% = 42,5% - мальчики
Ответ: 57,5%, 42,5%.

Задание 764

В санатории отдыхали мужчины и женщины. Мужчины составляли 40% всех отдыхающих. Какой процент всех отдыхающих составляли женщины?

Решение

100% − 40% = 60% всех отдыхающих составляли женщины
Ответ: 60%.

Задание 765

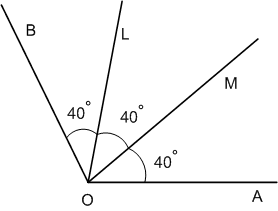
Выполните действия:
а) (3,8 * 1,75 : 0,95 − 1,02) : 2,3 + 0,4;
б) (11,28 + 3,4 : 0,85 * 1,55) : 4,6 − 0,8.

Решение

а) (3,8 * 1,75 : 0,95 − 1,02) : 2,3 + 0,4 = (7 − 1,02) : 2,3 + 0,4 = 2,6 + 0,4 = 3

б) (11,28 + 3,4 : 0,85 * 1,55) : 4,6 − 0,8 = (11,28 + 6,2) : 4,6 − 0,8 = 3,8 − 0,8 = 3

 

Пункт 41. Угол. Прямой и развернутый угол. Чертежный треугольник

Задание 766

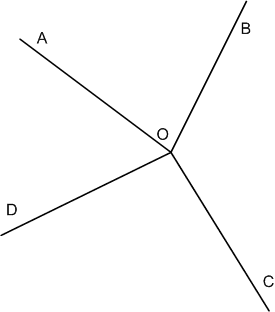
Назовите углы, изображённые на рисунке 168. Запишите их обозначения.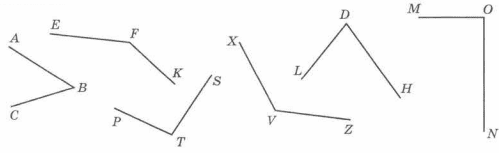

Решение

∠ABC, ∠EFK, ∠PTS, ∠XVZ, ∠LDH, ∠MON.

Задание 767

Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость?

Решение

Шесть углов: ∠АОВ, ∠AOC, ∠AOD, ∠BOC, ∠BOD, ∠COD.
Лучи делят плоскость на 4 части.

Задание 768

Укажите, какие точки на рисунке 169 лежат внутри угла КОМ. Какие точки лежат вне этого угла? Какие точки лежат на стороне ОК, a какие − на стороне ОМ?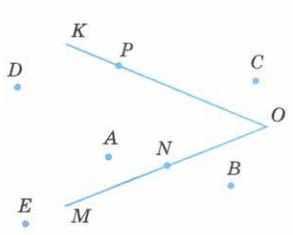

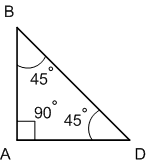
Решение

Внутри угла КОМ лежат точки А и D. Вне угла лежат точки В и С.
На стороне ОК лежит точка Р. На стороне ОМ лежат точки N и Е.

Задание 769

Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD.

Решение

Луч ОТ делит ∠MOD = ∠MOT + ∠TOD.

Задание 770

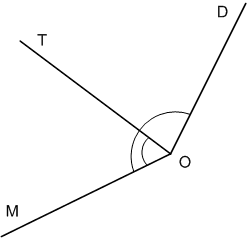
Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин − на угол ВОС, а ещё за 15 мин − на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170).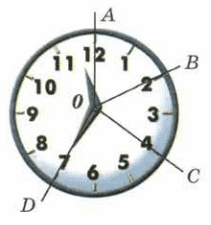

Решение

∠AOB = ∠BOC, ∠COD < ∠BOC, ∠AOC > ∠AOB, ∠AOC > ∠COD.

Задание 771

Изобразите с помощью чертёжного треугольника 4 прямых угла в разных положениях.

Решение

Задание 772

С помощью чертёжного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения.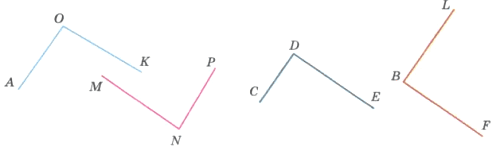

Решение

∠CDE и ∠FBL − прямые.

Задание 773

Укажите прямые углы в классной комнате.

Решение

Углы столов, углы стен и потолка и др.

Задание 774

Начертите прямоугольник со сторонами 6 см и 4 см и квадрат со стороной 7 см.

Решение

Задание 775

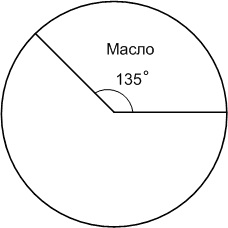
С помощью чертёжного треугольника начертите две прямые, которые при пересечении образуют прямые углы. На сколько частей они делят плоскость? Сколько развёрнутых углов на чертеже?

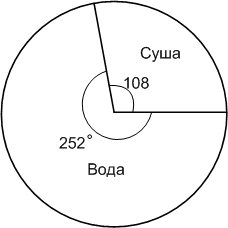
Решение

Четыре прямых угла ∠AOD, ∠AOC, ∠DOB, ∠BOC делят плоскость на четыре части.
Развёрнутые углы − ∠AOB и ∠DOC.

Задание 776

Начертите круг с центром О и радиусом 4,5 см. Разделите круг на четыре доли и закрасьте 3/4 круга.

Решение

Задание 777

Вычислите устно:
а) 8,1 - 0,9
: 8
* 0,2
+ 0,22
?
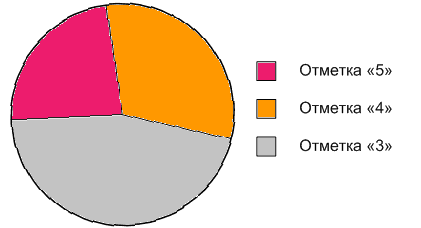
б) 0,62 - 0,4
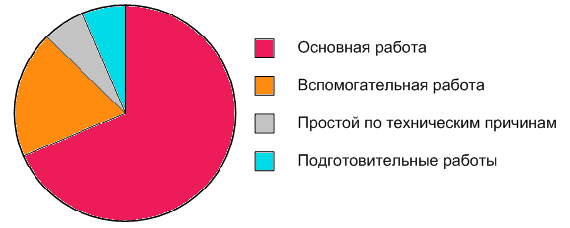
: 0,2
+ 3,4
* 2
?
в) 4,8 : 6
* 5
* 0,4
: 0,8
?
г) 7 : 100
+ 0,33
* 50
- 0,9
?
д) 1,25 : 5
+ 1,2
* 0,3
?

Решение

а) 7,2, 0,9, 0,18, 0,4.

б) 0,22, 1,1, 4,5, 9.

в) 0,8, 4, 1,6, 2.

г) 0,07, 0,4, 20, 19,1.

д) 2,5, 0,5, 1,7, 0,51.

Задание 778

Уменьшится или увеличится число, если его:
а) умножить на 2,5; 0,7; 0,01; 1,001;
б) разделить на 2,5; 0,7; 0,01; 1,001?

Решение

а) При умножении на 2,5 и 1,001 исходное число увеличится, а при умножении на 0,7; 0,01 исходное число уменьшится.

б) При делении на 2,5 и 1,001 частное меньше делимого, а при делении на 0,7; 0,01 частное больше делимого.

Задание 779

Расскажите, как найти 7% числа а. Найдите:
а) 8% от 400;
б) 30% от 20;
в) 10% от 46;
г) 25% от 28;
д) 20% от 5.

Решение

а) 400 : 100 * 8 = 32

б) 20 : 100 * 30 = 6

в) 46 : 100 * 10 = 4,6

г) 28 : 100 * 25 = 7

д) 5 : 100 * 20 = 1

Задание 780

Найдите число, если 5% этого числа равны:
20; 40; 100; 0,1; 0,6; 1,5.

Решение

20 : 5 * 100 = 400
40 : 5 * 100 = 800
100 : 5 * 100 = 2000
0,1 : 5 * 100 = 2
0,6 : 5 * 100 = 12
1,5 : 5 * 100 = 30

Задание 781

Составьте задачу по числовому выражению:
а) 0,09 * 200;
б) 208 * 0,4;
в) 130 * 0,1 + 80 * 0,1.

Решение

а) В 200 грамм раствора содержится 9% твердого вещества. Сколько грамм твердого вещества содержится в растворе?

0,09 * 200 = 18 (г) - твердого вещества в растворе
Ответ: 18 г.

б) Поле площадью 208 га на 40% засеяно пшеницей. Сколько га пшеницы засеяно?

208 * 0,4 = 83,2 (га) - занимает пшеница
Ответ: 83,2 га.

в) У Пети было 130 рублей, а у Васи 80 рублей. Сколько рублей потратили вмести мальчики в магазине, если каждый из них потратил 10% от имеющихся у них денег?

130 * 0,1 + 80 * 0,1 = 13 + 8 = 21 (р.) - потратили вместе мальчики
Ответ: 21 рубль.

Задание 782

Сколько процентов от 400 составляет число
200; 100; 4; 40; 80; 400; 600?

Решение

(200 : 400) * 100% = 50%
(100 : 400) * 100% = 25%
(4 : 400) * 100% = 1%
(40 : 400) * 100% = 10%
(80 : 400) * 100% = 20%
(400 : 400) * 100% = 100%
(600 : 400) * 100% = 150%

Задание 783

Найдите пропущенное число:
а)         б)
2 5 3    2 3 5
1 3 6    1 2 1
2 3 ?    4 2 ?

Решение

а) Число − 5. Правило: сумма чисел в строке равна 10.

б) Число − 1. Правило: сумма чисел в столбце равна 7.

Задание 784

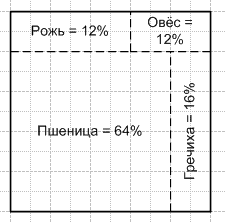
Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овёс − 8%, пшеница − 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?

Решение

2 * 8 = 16% поля занимает гречиха
Ответ: 16%.

Задание 785

За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года?

Решение

100% - 40% = 60 % - тетрадей осталось у Пети
30 т. составляют 60%
60% = 0,6
30 : 0,6  = 50 (т.) - осталось у Пети
Ответ: 50 тетрадей.

Задание 786

Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?

Решение

1) 6 + 34 = 40 (кг) - масса сплава
2) 34 : 40 = 0,85 сплава составляет медь
0,85 = 85%
Ответ: 85%.

Задание 787

Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м. Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.

Решение

Пусть x − высота башен Московского Кремля равна,
тогда высота Александрийского, маяка − 1,7x м,
высота здания Московского университета − (1,7x + 119) м.
Александрийский маяк выше башен Кремля на (1,7x − х) м.
Составим уравнение:
(1,7x − х) = 49
x = 49 : 0,7
х = 70
Значит, высота башен Кремля 70 м,
1,7 * 70 = 119 (м) - высота Александрийского маяка
119 + 119 = 238 (м) - высота здания Московского университета
Ответ: 70 м, 119 м, 238 м.

Задание 788

Найдите с помощью микрокалькулятора:
а) 4,5% от 168;
б) 147,6% от 2500;
в) 28,3% от 569,8;
г) 0,09% от 456800.

Решение

а) 168 : 100 * 4,5 = 1,68 * 4,5 = 7,56

б) 2500 : 100 * 147,6 = 25 * 147,6 = 3690

в) 569,8 : 100 * 28,3 = 5,698 * 28,3 = 161,2534

г) 456800 : 100 * 0,09 = 4568 * 0,09 = 411,12

Задание 789

Решите задачу:
1) Площадь огорода 6,4 а. В первый день вскопали 30% огорода, а во второй день − 35% огорода. Сколько аров осталось ещё вскопать?
2) У Серёжи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него ещё осталось?

Решение

1)
30% + 35% = 65% огорода вскопали всего
100% − 65% = 35% огорода осталось вскопать
6,4 : 100 * 35 = 2,24 (а) - осталось вскопать
Ответ: 2,24 а.

2)
35% + 40% = 75% времени потратил Сережа
100% − 75% = 25% свободного времени у него осталось
4,8 : 100 * 25 = 1,2 (ч) - свободного времени
Ответ: 1,2 ч.

Задание 790

Выполните действия:
1) ((23,79 : 7,8 − 6,8 : 17) * 3,04 − 2,04) * 0,85;
2) (3,42 : 0,57 * 9,5 − 6,6) : ((4,8 − 1,6) * (3,1 + 0,05)).

Решение

1) ((23,79 : 7,8 − 6,8 : 17) * 3,04 − 2,04) * 0,85 = (8,056 − 2,04) * 0,85 = 6,016 * 0,85 = 5,1136

2) (3,42 : 0,57 * 9,5 − 6,6) : ((4,8 − 1,6) * (3,1 + 0,05) = (57 − 6,6) : 10,08 = 50,4 : 10,08 = 5

Задание 791

Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла.

Решение

Задание 792

Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК?
Какая точка лежит внутри угла АМВ, но вне угла АМК? Какие точки лежат на сторонах угла АМК?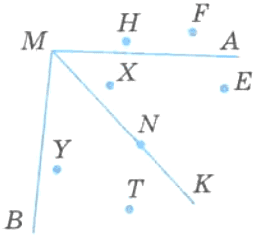

Решение

Внутри ∠AMK лежат точки X и Е.
Точки У и Т лежат внутри ∠AMB, но вне ∠AMК.
Точка N лежит на стороне ∠АМК.

Задание 793

Найдите с помощью чертёжного треугольника прямые углы на рисунке 173.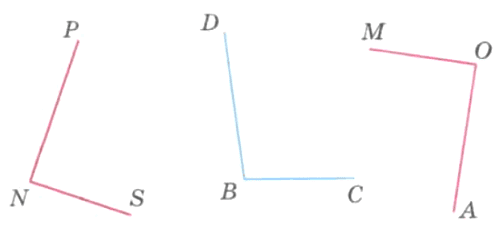

Решение

∠PNS и ∠МОА.

Задание 794

Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь.

Решение

P = 4 * 43 = 172 мм 17,2 см;
S = 43 * 43 = 1849 мм² = 18,49 см².

Задание 795

Найдите значение выражения:
а) 14,791 : а + 160,961 : b, если а = 100, b = 10;
б) 361,62с + 1848 : d, если с = 100, d =100.

Решение

а) При а = 100 и b = 10
14,791 : а + 160,961 : b = 14,791 : 100 + 160,961 : 10 = 0,14791 + 16,0961 = 16,24401

б) При с = 100 и d = 100
361,62с + 1848 : d = 361,62 * 100 + 1848 : 100 = 36162 + 18,48 = 36180,48

Задание 796

Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные − во второй. Сколько деталей изготовил рабочий во второй день?

Решение

100% − 60% = 40% деталей изготовил рабочий во второй день
450 : 100 * 40 = 180 (д.) - изготовил рабочий во второй день
Ответ: 180 деталей.

Задание 797

В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке?

Решение

1) 8000 + 2000 = 10000 (к.) - стало через год
2) 10000 : 8000 * 100% = 125% - книг стало в библиотеке
3) 125% − 100% = 25% - на столько увеличилось количество книг
Ответ: на 25%.

Задание 798

Грузовики в первый день проехали 24% намеченного пути, во второй день − 46% пути, а в третий − остальные 450 км. Сколько километров проехали эти грузовики?

Решение

1)100% − (24% + 46%) = 100% − 70% = 30% всего пути проехали грузовики в третий день
450 км составляет 30%
30% = 0,3
2) 450 : 0,3 = 1500 (км) - проехали грузовики
Ответ: 1500 км.

Задание 799

Найдите, сколько составляют:
а) 1% от тонны;
б) 1% от литра;
в) 5% от 7 т;
г) 6% от 80 км.

Решение

а) 1 т = 1000 кг, 1000 кг : 100 = 10 кг.

б) 1 л = 1000 с м 3 , 1000 с м 3 : 100 = 10 с м 3.

в) 7 т = 7000 кг, 7000 кг : 100 * 5 = 350 кг.

г) 80 км = 80000 м, 80000 м : 100 * 6 = 4800 м.

Задание 800

Масса детёныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детёнышем их масса равна 0,9 т?

Решение

Пусть х − масса детёныша, тогда 9у − масса взрослого моржа.
Составим уравнение:
у + 9у = 900
у = 90 : 10
y = 90
Значит, масса детёныша 90 кг
9 * 90 = 810 (кг) - масса взрослого моржа
Ответ: 810 кг.

Задание 801

Во время манёвров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?

Решение

Пусть солдат во втором отряде было х,
тогда в первом отряде было 6х солдат.
Составим уравнение:
х + 6х = 200 * (1 − 0,3)
7х = 140
х = 140 : 7
х = 20
Значит, 20 солдат было во втором отряде
6 * 20 = 120 (с.) - было в первом отряде
Ответ: 120 солдат.

 

Пункт 42. Измерение углов. Транспортир

Задание 802

По рисунку 178 определите градусные меры углов:
а) AKD, АКБ, AKF;
б) BKF, ВКЕ, ВКС, BKD;
в) DKC, DKE, DKF, СКЕ, CKF и EKF.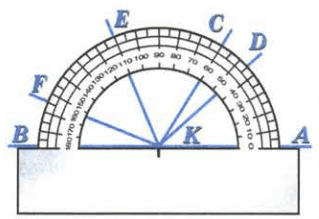

Решение

а) ∠AKD = 45°, ∠AKE = 110°, ∠AKF = 155°.

б) ∠BKF = 25°, ∠BKE = 70°, ∠BKE = 120°, ∠BKD = 135°.

в) ∠DKC = 60° − 45° = 15°, ∠DKE = 110° − 45° = 65°, ∠DKF = 155° − 45° = 110°, ∠CKE = 110° − 60° = 50°, ∠CKF = 155°− 60° = 95°, ∠EKF = 155° − 110° = 45°.

Задание 803

Начертите луч ОА. С помощью транспортира по одну сторону от луча ОА постройте:
∠AOB = 45°, ∠AOC = 30°, ∠AOD = 135°, ∠AOE = 90°.

Решение

∠AOB = 45°, ∠AOC = 30°, ∠AOD = 135°, ∠AOE = 90°.

Задание 804

Измерьте углы, изображённые на рисунке 179, и запишите результаты измерений.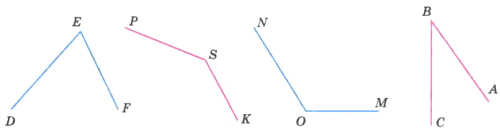

Решение

LDEF = 75°, ∠PSK = 135°, ∠NOM = 112°, ∠ABC = 50°.

Задание 805

Луч ОС лежит внутри угла АОВ, причём ∠AOC = 37°, ∠BOC = 19°. Чему равен угол АОВ?

Решение

∠AOB = ∠АОС + ∠BOC = 37° + 19° = 56°.

Задание 806

Какую часть развёрнутого угла составляют углы в 30°; 45°; 60°?
Какую долю прямого угла составляют углы в 30°; 15°; 60°; 75°?

Решение

30 ° = 30 : 180 = 1/6
45 ° = 45 : 180 = 1/4
60 ° = 60 : 180 = 1/3

30 ° = 30 : 90 = 1/3
15 ° = 15 : 90 = 1/6
60 ° = 60 : 90 = 2/3
75 ° = 75 : 90 = 5/6

Задание 807

Сколько градусов содержит угол, если он составляет:
а) 1/2 развёрнутого угла;
б) 1/3 развёрнутого угла;
в) 5/6 прямого угла;
г) 3/5 прямого угла;
д) 0,1 прямого угла;
е) 0,2 развёрнутого угла?

Решение

а) 1/2 * 180 ° = 180 ° : 2 = 90 °

6) 1/3 * 180 ° = 180 ° : 3 = 60 °

в) 5/6 * 90 ° = 90 ° : 6 * 5 = 75 °

г) 3/5 * 90 ° = 90 ° * 3 : 5 = 54 °

д) 0,1 * 90° = 9°

e) 0,2 * 180° = 36°

Задание 808

Сколько градусов содержит угол, если он составляет:
а) 20% от 360°;
б) 25% от 60°;
в) 45% развёрнутого угла;
г) 80% прямого угла?

Решение

а) 360° : 100 * 2 = 72°

б) 60° : 100 * 25 = 15°

в) 180° : 100 * 45 = 81°

г) 90° : 100 * 80 = 72°

Задание 809

Какой угол образуют часовая и минутная стрелки часов:
а) в 3 ч;
б) в 5 ч;
в) в 10 ч;
г) в 11 ч;
д) в 2 ч 30 мин;
е) в 5 ч 30 мин?

Решение

а) в 3 ч − угол 90°

б) в 5 ч − угол 180° : 6 * 5 = 150°

в) в 10 ч − угол 180° : 6 * 2 = 60°

г) в 11 ч − угол 180° : 6 = 30°

д) в 2 ч 20 мин − угол 120° − 70° = 50°

е) в 5 ч 30 мин − угол 180° − 165° = 15°

Задание 810

Постройте с помощью транспортира угол 70° и проведите луч, который делит угол пополам.
Такой луч называется биссектрисой угла.

Решение

Задание 811

С помощью транспортира проведите луч, который делит пополам прямой угол.

Решение

Задание 812

Постройте угол АОВ в 120° и разделите его на 3 равных угла.

Решение

Задание 813

Какие из углов острые и какие тупые, если ∠A = 67°; ∠B = 175°; ∠C = 92°; ∠D = 3°?

Решение

Острые углы: ∠A = 67°, ∠D = 3°.
Тупые углы: ∠B = 175°, ∠C = 92°.

Задание 814

С помощью чертёжного треугольника найдите на рисунке 180 острые, прямые и тупые углы. С помощью транспортира найдите их градусную меру.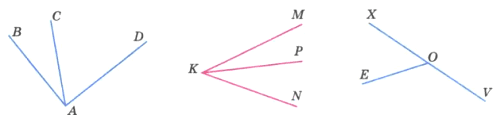

Решение

Острые углы: ∠BAC = 20°, ∠CAD = 70°, ∠PKM = 20°, ∠PKN = 38°, ∠MKN = 58°, ∠XOE = 55°.
Прямой угол: ∠BAD = 90°.
Тупой угол: ∠EOV = 25°.
Развернутый угол ∠XOV = 180°.

Задание 815

Начертите круг радиусом 3 см. Обозначьте его центр буквой О. Проведите через точку О прямую АВ. С помощью транспортира разделите развёрнутые углы AОВ с обеих сторон прямой на 3 равных угла. На сколько равных частей разделился круг?

Решение

Круг разделен на 6 равных частей.

Задание 816

Угол АОВ развёрнутый, а ОС − луч. Найдите градусные меры углов АОС и СОВ, если:
а) градусная мера угла АОС втрое больше, чем градусная мера угла СОВ;
б) градусная мера угла АОС на 60° больше градусной меры угла СОВ;
в) градусная мера угла АОС в 4 раза меньше, чем градусная мера угла СОВ.

Решение

а) Пусть ∠COB = x°, тогда ∠AOC = 3x°.
Сумма ∠COB + ∠AOC = ∠AOB = (x + 3х)°.
Составим уравнение:
х + 3х = 180
х = 180 : 4
х = 45°
∠COB = 45°, ∠AОС = 3 * 45 = 135°.

б) Пусть ∠COB = х°, тогда ∠AOC = (x + 60)°.
Сумма ∠COB + ∠AOC = ∠AOB = (х + x + 60)°.
Составим уравнение:
x + х + 30 = 180
x = (180 − 60) : 2
х = 60°
∠COB = 60°, ∠AOC = 60 + 60 = 120°.

в) Пусть ∠AOC = х°, тогда ∠COB = 4х°.
Сумма ∠COB + ∠AOC = ∠AOB = (х + 4x)°.
Составим уравнение:
х + 4х = 180
x = 180 : 5°
x = 36°
∠AOC = 36°, ∠COB = 4 * 36 = 144°.

Задание 817

Внутри прямого угла АОВ проведён луч ОС. Найдите градусные меры углов АОС и СОВ, если:
а) угол АОС в 5 раз больше угла СОВ;
б) разность градусных мер углов СОВ и АОС равна 46°;
в) угол АОС в 4 раза меньше угла СОВ.

Решение

а) Пусть ∠COB = x°, тогда ∠AOC = 5х°.
Сумма ∠COB + ∠AOC = ∠AOB = (х + 5х) градусов.
Составим уравнение:
х + 5x = 90
х = 90 : 6
х = 15°
∠COB = 15°, LAOC = 5 * 15 = 75°.

б) Пусть ∠COB = x°, тогда ∠AOC = (90 − x)°.
Сумма ∠COB + ∠AOC = ∠AОВ = (x − (90 − x)°.
Составим уравнение:
х − (90 − х) = 46
х + х − 90 = 46
х = (46 + 90) : 2
х = 68°
∠COB = 68°, ∠AOC = 90 − 68 = 22°.

в) Пусть ∠AOC = х°, тогда ∠СОВ = 4х°.
Сумма ∠COB + ∠AOC = ∠AOB = (x + 4x)°.
Составим уравнение:
x + 4х = 90
x − 90 : 5
х = 18°
∠AOC = 18°, ∠COB = 4 * 18° = 72°.

Задание 818

Чему равна градусная мера каждого угла прямоугольника? Чему равна сумма этих градусных мер? Чему равна сумма градусных мер углов каждого из треугольников ABC и CDA (рис. 181)?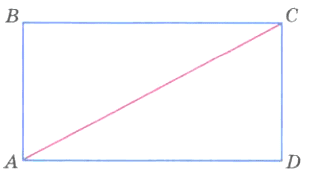

Решение

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
∠AВС + ∠BCD + ∠CDA + ∠DAB = 90° + 90° + 90° + 90° = 360°
∠ABC + ∠ВСА + ∠CAB = 180°
∠ACD + ∠CDA + ∠DAC = 180°

Задание 819

Измерьте каждый угол треугольника ACD, изображённого на рисунке 182, Найдите сумму градусных мер этих углов.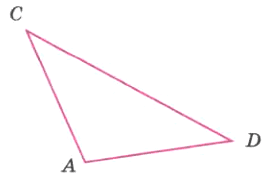

Решение

∠CAD = 110°, ∠ADC = 35°, ∠ACD = 35°
∠CAD + ∠ADC + ∠ACD = 110° + 35° + 35° = 180°

Задание 820

Начертите какой−нибудь треугольник и измерьте каждый его угол.
Проверьте, что сумма градусных мер углов треугольника равна 180°.
Запомните это свойство углов треугольника.

Решение

∠BAD + ∠ABD + ∠BDA = 90° + 45° + 45° = 180°

Задание 821

В треугольнике один из углов равен 75°, а другой − 80°. Чему равен третий угол этого треугольника?

Решение

180° − (75° + 80°) = 180° − 155° = 25°

Задание 822

В треугольнике ABC градусная мера угла ABC равна 40°, а градусная мера угла CAB в 3 раза больше. Найдите градусную меру угла АСВ.

Решение

∠АСВ = 180° − (∠ABC + ∠CAB) = 180° − (40° + 3 * 40°) = 180° − 160 = 20°

Задание 823

Вычислите устно:
а) 2,8 + 0,70
: 5
* 90
-3,5
?
б) 6 - 1,2
: 8
* 9
+ 1,9
?
в) 8,7 : 3
+ 2,6
- 1,5
* 0,6
?
г) 0,4 * 5
- 0,01
+ 0,28
: 0,15
?
д) 14 : 70
* 1,5
+ 3,7
* 0,25
?

Решение

а) 3,5, 0,7, 63, 59,5.

б) 4,8, 0,6, 5,4, 7,3.

в) 2,9, 5,5, 4, 2,4.

г) 2, 0,02, 0,3, 2.

д) 0,2, 0,3, 4, 1.

Задание 824

Назовите каждый из углов, изображённых на рисунке 183, а и б. Найдите среди этих углов прямые и развёрнутые углы.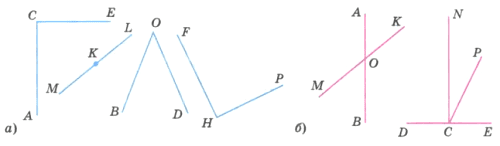

Решение

Углы: ∠АСЕ, ∠МКР, ∠BOD, ∠FHL, ∠ВОМ,
∠МОА, ∠АОК, ∠КОВ, ∠МОК, ∠АОВ, ∠ВСЕ, ∠DCN, ∠DCP, ∠NCP, ∠РСЕ, ∠NCE.
Прямые углы: ∠АСЕ, ∠FHP.
Развернутые углы: ∠МКР, ∠МОК, ∠AOB, ∠DCE.

Задание 825

Найдите 5%, 15%, 25%, 45% числа 360. Попробуйте предложить разные способы решения этой задачи.

Решение

360 : 100 * 5 = 360 : 20 = 18
360 : 100 * 15 = 18 * 3 = 54
360 : 100 * 25 = 360 : 4 = 90
360 : 100 * 45 = 18 * 9 =162

Задание 826

5% некоторого числа равны 11. Найдите 15%, 20%, 35%, 50%, 100% этого числа.

Решение

Число равно 11 : 5 = 100 = 220
220 : 100 * 15 = 33
220 : 100 * 20 = 44
220 : 100 * 35 = 77
220 : 100 * 50 = 110
220 : 100 * 100 = 220

Задание 827

В зале кинотеатра 600 зрителей.
а) Сколько человек составляют 1%, 5%, 10%, 40% всех зрителей?
б) Сколько процентов зрителей составляют 12 человек, 90 человек, 300 человек?

Решение

а) 600 : 100 * 1 = 6
600 : 100 * 5 = 30
600 : 100 * 10 = 60
600 : 100 * 40 = 240

б) (12 : 600) * 100% = 2%
(90 : 600) * 100% = 15%
(300 : 600) * 100% = 50%

Задание 828

а) Число 60 увеличили на 15. На сколько процентов увеличилось число?
б) Число 75 уменьшили на 15. На сколько процентов уменьшилось число?
в) Некоторое число увеличили в 2 раза. На сколько процентов увеличилось число?
г) Некоторое число уменьшили в 2 раза. На сколько процентов уменьшилось число?

Решение

а) 60 + 15 = 75
(75 : 60) * 100% = 125%
125% − 100% = 25%

б) 75 − 15 − 60
(60 : 75) * 100% = 80%
100% − 80% = 20%

в) 2х : х * 100% = 200
200% − 100% = 100%

г) 0,5х : х * 100% = 50
100% − 50% = 50%

Задание 829

Найдите пропущенные числа:

Решение

а) Число: 0,8/3,6.
Правило: числитель каждой следующей дроби на 0,1 меньше числителя предыдущей дроби, а знаменатель каждой следующей дроби на 0,8 больше знаменателя предыдущей дроби.

б) Число: 0,05/0,15.
Правило: числитель и знаменатель каждой дроби через одну в 4 раза меньше числителя и знаменателя предыдущей дроби через одну.

Задание 830

Стреляя в тире, Дима в 76% случаев попал в мишень. Сколько промахов допустил Дима, если всего он произвёл 50 выстрелов?

Решение

1) 100% − 76% = 24% случаев Дима не попал в мишень
2) 50 : 100 * 24 = 12 (п.) - совершил Дима
Ответ: 12 промахов.

Задание 831

За три дня в магазине продано 1280 кг яблок. В первый день продали 25% всех яблок, а во второй день − 45% всех яблок. Сколько килограммов яблок продали в третий день? Решите задачу двумя способами. Какой из этих способов проще?

Решение

1 способ.
    25% = 0,25
1) 1280 * 0,25 = 320 (кг) - яблок продано в первый день
    45% = 0,45
2) 1280 * 0,45 = 576 (кг) - яблок продано во второй день
3) 1280 − (320 + 576) = 1280 − 896 = 384 (кг) - яблок продано в третий день
Ответ: 384 кг.

2 способ.
1) 100% − (25% + 45%) = 100% − 70% = 30% всех яблок продано в третий день
2) 1280 : 100 * 30 = 384 (кг) - яблок  продано в третий день
Ответ: 384 кг.

Второй способ решения проще первого.

Задание 832

Объясните смысл предложения:
а) «Из молока получается 25% сливок»;
б) «В свёкле содержится 20% сахара».

Решение

а) Это означает, что из х л молока получается 0,25x л сливок.

б) Это означает, что из х кг свёклы получается 0,2х кг сахара.

Задание 833

При перегонке нефти получается 30% керосина. Сколько керосина можно получить из 12 т; из 28 т; из 36,5 т нефти?

Решение

30% = 0,3
1) 12 * 0,3 = 3,6 (т) - керосина получается из 12 т нефти
2) 28 * 0,3 = 8,4 (т) - керосина получается из 28 т нефти
3) 36,5 * 0,3 = 10,95  (т) - керосина получается из 36,5 т нефти
Ответ: 3,6 т, 8,4 т, 10,95  т.

Задание 834

Решите задачу:
1) Площадь поля 560 га. В первый день засеяли 3/7 поля, а остальное − во второй день.
Сколько гектаров засеяли во второй день?
2) Площадь поля 450 га. Овсом засеяли 2/5 поля, а пшеницей − остальную часть.
Сколько гектаров засеяли пшеницей?

Решение

1) 1 − 3/7 = 4/7 всего поля  засеяли во второй день,
     560 * 4/7 = 80 * 4 = 320 (га) -  асеяли во второй день
Ответ: 320 га.

2) 1 − 2/5 = 3/5 поля засеяли пшеницей
    450 * 3/5 = 90 * 3 = 270 (га) - засеяли пшеницей
Ответ: 270 га.

Задание 835

Начертите два угла − в 60° и в 100° − с общей вершиной так, чтобы они имели общую сторону и лежали по разные стороны от неё. Найдите градусную меру угла, образованного двумя другими сторонами этих углов.

Решение

∠AOB = 60°, ∠AOC = 100°, ∠BOC = 100° + 60° = 160°.

Задание 836

Начертите произвольный четырёхугольник ABCD, измерьте транспортиром его углы и сложите результаты измерений.

Решение

∠DAB = 90°, ∠CDA = 90°, ∠ABC = 90°, ∠BCD = 90°;
∠DAB + ∠CDA + ∠ABC + ∠BCD = 90° + 90° + 90° + 90° = 360°.

Задание 837

Начертите произвольный четырёхугольник ABCD и проведите прямые АС и BD. Измерьте транспортиром углы АОВ, ВОС, COD и DOA, где О − точка пересечения прямых АС и BD. Какие из этих углов имеют одинаковую градусную меру? Сумма градусных мер каких углов равна 180°?

Решение

∠COD = 90°,
∠BOC = 90°,
∠AOB = 90°,
∠AOD = 90°,
∠AOB = ∠COD, ∠BOC = ∠AOD;
∠AOB + ∠BOC = ∠BOC + ∠COD = ∠COD + ∠DOA = ∠AOD + ∠AOB = 180°.

Задание 838

Найдите градусные меры углов треугольника MNKy если угол М меньше угла N на 40° и больше угла К на 10°.

Решение

Пусть градусная мера ∠M равна х, тогда ∠N = (х + 40)°, а ∠К = (х − 10)°.
Составим уравнение:
x + x + 40 + x − 10 = 180
3x + 30 = 180
х = (180 − 30) : 3
х = 50°.
∠M = 50°, ∠N = 50 + 40 = 90°, ∠K = 50 − 10 = 40°.

Задание 839

Найдите градусные меры углов треугольника CDE, если угол С вдвое больше угла D и втрое меньше угла Е.

Решение

Пусть ∠D = х°, тогда ∠C = 2х°, a ∠E = 3 * 2х°.
Составим уравнение:
х + 2х + 3 * 2х = 180
х = 180 : 9
х = 20°.
∠D = 20°, ∠C = 2 * 20 = 40°, ∠E = 3 * 40 = 120°.

Задание 840

В механическом цехе установлено 400 станков. В первую смену работало 380 станков, а во вторую − 350 станков. Какой процент станков работал в первую смену и какой во вторую?

Решение

1)   (380 : 400) * 100% = 95% всех станков работало в первую смену,
2)   (350 : 400) * 100% = 87,5% всех станков работало во вторую смену
Ответ:  95%, 87,5%.

Задание 841

Никелевая руда содержит 1,3% никеля. Сколько тонн никеля получится из 24 860 т руды? Сколько тонн этой руды надо переработать, чтобы добыть 2405 т никеля?

Решение

    1,3% = 0,013
    1,3% от 24 860 т
1)   24860 * 0,013 = 323,18 (т) - никеля получится из 24860 т руды
    2405 т составляют 1,3%
2)  2405 : 0,013 = 185 000 (т) руды надо переработать для добычи 2405 т никеля
Ответ: 323,18 т, 185 000 т.

Задание 842

Магнитный железняк содержит 70% чистого железа. Сколько тонн чистого железа содержится в 4,6 т магнитного железняка?

Решение

70% от  4,6 т
70% = 0,7
4,6 * 0,7 = 3,22 (т) - чистого железа содержится в 4,6 т магнитного железняка 
Ответ: 3,22 т.

Задание 843

Из чайного листа после сушки получается 4,2% чая. Сколько получится чая из 225 кг чайного листа?

Решение

4,2% от 225 кг
4,2% = 0,042
225 * 0,042 = 9,45 (кг) - чая получится из 225 кг чайного листа.
Ответ: 9,45 кг.

Задание 844

Привезли 500 т руды с содержанием меди 6,5% и 700 т руды с содержанием меди 4,5%. Из какой руды получится больше меди?

Решение

1)  500 : 100 * 6,5 = 32,5 (т) - меди получится из 500 т руды, содержащей 6,5% меди
2) 700 : 100 * 4,5 = 31,5 (т) - меди получится из 700 т руды, содержащейся 4,5% меди
Ответ:  из первой руды получится больше меди.

Второй способ оформления задачи:

6,5% от 500 т
6,5% = 0,065
1)  500 * 0,065 = 32,5 (т) - меди получится из 500 т руды, содержащей 6,5% меди
4,5% от 700 т
4,5% = 0,045
2) 700 * 0,045 = 31,5 (т) - меди получится из 700 т руды, содержащейся 4,5% меди
Ответ:  из первой руды получится больше меди.

Задание 845

С помощью микрокалькулятора найдите значение выражения:
а) 284,3 * 159,6 + 51 189,1 : 32,1 − 651,2 * 34,8;
б) 376,64 : 4,4 : 3,2 + 0,479 * 0,37 * 44,5.

Решение

а) 284,3 * 159,6 + 51189,1 : 32,1 − 651,2 • 34,8 = 45374,28 + 1594,676 − 22661,76 = 24307,196

б) 376,64 : 4,4 : 3,2 + 0,479 • 0,37 • 44,5 = 26,75 + 7,886735 = 34,636735

 

Пункт 43. Круговые диаграммы

Задание 846

Известно, что 3 8 массы льняного семени составляет масло. Постройте круговую диаграмму содержания масла в льняном семени.

Решение

360° * 3 : 8 = 45 * 3 = 135°

Задание 847

Вода занимает 0,7 всей поверхности земного шара. Постройте круговую диаграмму распределения воды и суши на земной поверхности.

Решение

360° * 0,7 = 252° на диаграмме будет занимать вода;
360° − 252° = 108° на диаграмме будет занимать суша.

Задание 848

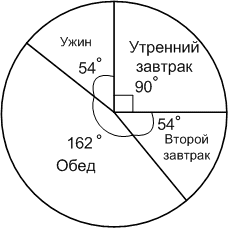
Врачи рекомендуют дневную норму питания распределить на 4 приёма: утренний завтрак − 25%, второй завтрак − 15%, обед − 45% и ужин − 15%. Постройте круговую диаграмму распределения дневной нормы питания.

Решение

360° * 0,25 = 90° на диаграмме будет занимать сектор утреннего завтрака;
360° * 0,15 = 54° сектор второго завтрака;
360° * 0,45 = 162° сектор обеда;
360° * 0,15 = 54° сектор ужина.

Задание 849

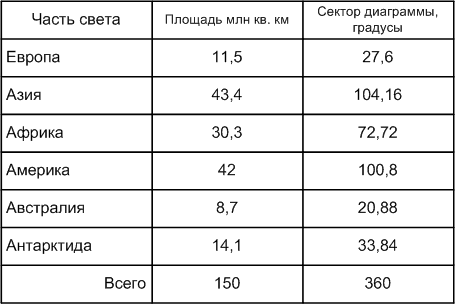
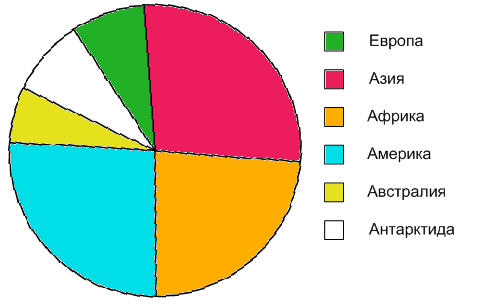
Постройте круговую диаграмму площадей частей света Земли, предварительно заполнив таблицу (используйте микрокалькулятор):

Решение

Задание 850

Вычислите устно:
а) 1 - 0,2
* 10
: 40
+ 3,8
?
б) 4,9 + 1,4
: 3
+ 3,9
: 12
?
в) 0,4 * 20
: 0,2
: 100
+ 2,6
?
г) 63 : 90
+ 0,5
* 4
- 0,9
?
д) 15 : 2,5
+ 2,1
: 2,7
- 0,6
?

Решение

а) 0,8, 8, 0,2, 4.

б) 6,3, 2,1, б, 0,5.

в) 8, 40, 0,4, 3;

г) 0,7, 1,2, 4,8, 3,9.

д) 6, 8,1, 3, 2,4.

Задание 851

Найдите:
а) 50% от 6 т; 1 ч; 1 дм; 90°;
б) 10% от 1 кг; 2000 р.; 1 а; 1 л; 180°.

Решение

а) 6 т * 50 : 100 = 3 т;
1 ч * 50 : 100 = 0,5 ч = 30 мин;
1 дм * 50 : 100 = 5 см;
90° * 50 : 100 = 45°.

б) 1 кг * 10 : 100 = 1000 г *10 : 100 = 100 г;
2000 p. * 10 : 100 = 200 p.;
1 a * 10 : 100 = 100 м² * 10 : 100 = 10 м²;
1 л * 10 : 100 = 1000 см³ * 10 : 100 = 100 см³;
180° * 10 : 100 = 18°.

Задание 852

Сколько процентов составляют:
а) 8 кг от 1 ц;
б) 15 с от 1 мин;
в) 35 см от 1 м;
г) 100 л от 1 м³?

Решение

а) 1 ц = 100 кг, (8 : 100) * 100% = 8%

б) 1 мин = 60 с, (15 : 60) * 100% = 25%

в) 1 м = 100 см, (35 : 100) * 100% = 35%

г) 1 м³ = 1000 л, (100 : 1000) * 100% = 10%

Задание 853

Найдите число, если:
а) 1% этого числа равен 1; 6; 0,7; 1,8;
б) 10% этого числа равны 0,3; 1; 15; 2,4;
в) 25% этого числа равны 2; 10; 25; 0,5; 1,2.

Решение

а) Если 1% числа равен х, то число равно х : 100 * 100 = 100х:
при х = 1 => 100 * 1 = 100;
при х = 6 => 100 * 6 = 600;
при х = 0,7 => 100 * 0,7 = 70;
при х = 1,8 => 100 * 1,8 = 180.

б) Если 10% числа равны х, то число равно х : 10 * 100 = 10х:
при х = 0,3 => 10 * 0,3 = 3;
при х = 1 => 10 * 1 = 10;
при х = 15 => 10 * 15 = 150;
при х = 2,4 => 10 * 2,4 = 2,4.

в) Если 25% числа равно х, то число равно х : 100 * 25 = 4х:
при х = 2 => 4 * 2 = 8;
при х = 10 => 4 * 10 = 40;
при х = 25 => 4 * 25 = 100;
при х = 0,5 => 4 * 0,5 = 2;
при х = 1,2 => 4 * 1,2 = 4,8.

Задание 854

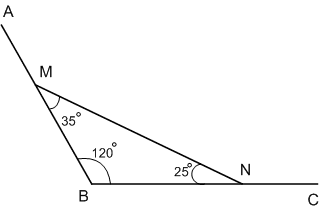
Вычислите градусную меру угла АОВ, используя рисунок 186.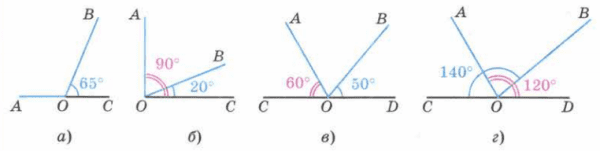

Решение

а) ∠AOB = 180° − 65° = 115°

б) ∠AOB = 90° − 20° = 70°

в) ∠AOB = 180° − (60° + 50°) = 180° − 110° = 70°

г) ∠BOD = 180° − 140° = 40°;
∠COA = 180° − 120° = 60°;
∠AOB = 180° − (40° + 60°) = 180° − 100° = 80°.

Задание 855

ABCD − прямоугольник, ∠ACB = 30° (рис. 187). Найдите градусную меру углов: ACD, ВАС, CAD.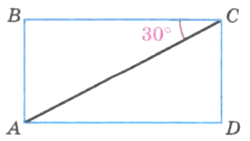

Решение

∠ACD = 90° − 30° = 60°;
∠ВАС = 180° − (90° + 30°) = 180° − 120° = 60°,
∠CAD = 90° − 60° = 30°.

Задание 856

Начертите угол ABC, равный 120°. На стороне ВА отложите отрезок ВМ, равный 3 см, а на стороне ВС − отрезок BN, равный 4 см. Соедините отрезком точки М и N. Измерьте стороны и углы получившегося треугольника и найдите периметр и сумму градусных мер углов этого треугольника.

Решение

ВM = 3 см, BN = 4 см, MN = 6 см,
PMBN = 3 + 4 + б = 13 см;
∠MBN = 120°, ∠BMN = 35°, ∠BNM = 25°,
∠MBN + ∠BMN + ∠BNM = 120° + 35°+ 25° = 180°.

Задание 857

В треугольнике ABC ∠A = 50°, a ∠B = 30°. Вычислите градусную меру угла С.

Решение

∠C = 180° − (50° + 30°) = 180° − 80° = 100°.

Задание 858

Молоко даёт 25% сливок, сливки дают 20% масла. Сколько масла получится из молока, надоенного за 15 дней от 360 коров, если каждая корова в среднем даёт 15 кг молока в день?

Решение

Получится 15 * 15 * 360 : 100 * 25 : 100 * 20 = 4050 кг масла.

Задание 859

Постройте круговую диаграмму распределения суши на Земле по следующим данным:

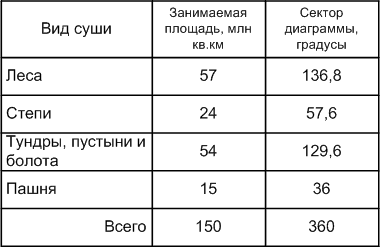
Решение

Задание 860

В классе 36 учеников. По математике за четверть отметку «5» имеют 8 человек, отметку «4» − 12 человек, а остальные − отметку «3». Постройте круговую диаграмму.

Решение

8 : 36 * 360° = 80° сектор отличников на диаграмме;
12 : 36 * 360° = 120° сектор ударников на диаграмме;
36 − (8 + 12) = 36 − 20 = 16 учеников получили отметку «3»,
16 : 36 * 360° = 160° сектор троечников на диаграмме.

Задание 861

Экипаж экскаватора работал 480 мин. Из них основная работа заняла 330 мин, вспомогательная работа − 90 мин, простой по техническим причинам − 30 мин и подготовительные работы − 30 мин. Постройте круговую диаграмму распределения рабочего времени этого экипажа.

Решение

330 мин : 480 мин * 360° = 247,5° сектор основной работы на диаграмме;
90 мин : 480 мин * 360° = 67,5° сектор вспомогательной работы на диаграмме;
30 мин : 480 мин * 360° = 22,5° сектор простоя по техническим причинам на диаграмме;
30 мин : 480 мин * 360° = 22,5° сектор подготовительных работ на диаграмме.

Задание 862

Велосипедист стал догонять пешехода, когда между ними было 2,1 км, и догнал его через 0,25 ч. Найдите скорость велосипедиста и скорость пешехода, если скорость пешехода была в 3,4 раза меньше скорости велосипедиста.

Решение

Пусть х − скорость пешехода, тогда скорость велосипедиста 3,4х км/ч.
Составим уравнение:
2,1 : (3,4х − х) = 0,25
2,4x = 2,1 : 0,25
х = 8,4 : 2,4 = 3,5 км/ч − скорость пешехода, а скорость велосипедиста равна 3,4 * 3,5 = 11,9 км/ч.

Задание 863

Сколько градусов содержит угол между часовой и минутной стрелками часов:
а) в 9 ч;
б) в 6 ч;
в) в 2 ч;
г) в 8 ч?

Решение

а) 90°

б) 180°

в) 180° : 3 = 60°

г) 180° : 3 * 2 = 120°