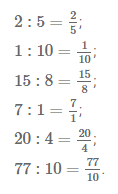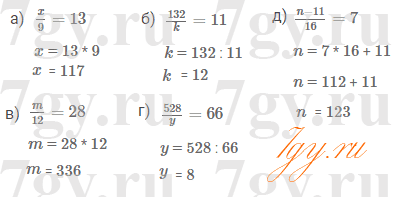Ответы к пункту 27. Деление и дроби, стр. 39
Задание № 202
Запишите в виде дроби частные:
2 : 5; 1 : 10; 15 : 8; 7 : 1; 20 : 4; 77 : 10.
Решение
Задание № 203
Запишите каждую из дробей 299/23,527/31 в виде частного и найдите его значение.
Решение
$\frac{299}{23}=299:23=13$
$\frac{527}{31}=527:31=17$
Задание № 204 с ответами
Заполните пустые клетки таблицы:
Задание № 205
За неделю израсходовано 3 кг сахара. Сколько килограммов сахара в среднем расходовали за один день?
Решение
3 : 7 = 3 (кг)
7
Ответ: 3/7 кг сахара в среднем расходовали за один день.
Задание № 206
Изделие на конвейере за 5 мин продвигается на 4 м. Найдите скорость движения конвейера.
Решение
4 : 5 = 4 (м/мин) = 400 см : 5 мин = 80 см/мин
5
Ответ: 80 см/мин.
Задание № 207
Из 4 м ткани сшили 7 юбок. Сколько ткани пошло на каждую юбку?
Решение
4 : 7=4 (м)
7
Ответ: 4/7 м ткани пошло на каждую юбку.
Задание № 208
Верёвку длиной в 7 м разрезали на 12 равных кусков. Найдите длину каждого куска.
Решение
7 : 12 = 7 (м)
12
Ответ: 7/12 м - длина каждого куска.
Задание № 209
Решите уравнение:
а) $\frac x9=13$
б) $\frac{132}k=11$
в) $\frac m{12}=28$
г) $\frac{528}y=66$
д) $\frac{n-11}{16}=7$
Решение уравнений
Задание № 210
Найдите значение выражения, применяя свойство деления суммы на число:
а) (48 + 80) : 16;
б) (3393 + 999) : 3;
в) 405 : 27 + 135 : 27;
г) 2926 : 19 + 874 : 19.
Решение
a) (48 + 80) : 16 = 48 : 16 + 80 : 16 = 3 + 5 = 8
б) (3393 + 999) : 3 = 3393 : 3 + 999 : 3 = 1131 + 333 = 1464
в) 405 : 27 + 135 : 27 = (405 + 135) : 27 − 540 : 27 = 20
г) 2926 : 19 + 874 : 19 = (2926 + 874) : 19 = 3800 : 19 = 200
Задание № 211
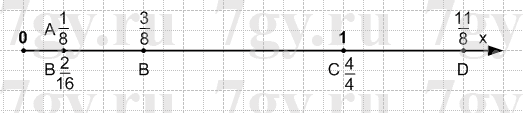
Расскажите, как на координатном луче отметить точки:
$A(\frac18),B(\frac38),C(\frac44),D(\frac{11}8),E(\frac2{16})$
Решение
Первым шагом необходимо выбрать единичный отрезок. Для удобства лучше выбрать отрезок, который является наименьшим общим кратным знаменателей указанных координат (в данном номере лучше выбрать за единичный отрезок 16 клеток тетради).
Для того чтобы узнать где на координатном луче поставить точку необходимо количество клеток, взятых за единичный отрезок, умножить на числитель координаты точки и поделить на знаменатель координаты точки. Получившийся результат будет показывать сколько клеток от начала координат Вам нужно отсчитать, чтобы поставить точку.
Например для точки A(1/8): 16 * 1 : 8 = 2 клетки тетради необходимо отсчитать вправо от начала координат, чтобы поставить точку А.
Задание № 212
Вычислите устно:
а) 55 - 47
* 9
- 34
: 19
* 24
?
б)
75 - 66
* 9
- 27
+ 18
: 18
?
в) 84 - 78
* 8
+ 12
: 5
* 30
?
г) 91 : 13
* 80
+ 240
- 500
: 15
?
д) 98 : 14
* 70
+ 210
: 35
* 15
?
Ответы
a) 8, 72, 38, 2, 48.
б) 7, 560, 800, 300, 20.
в) 9, 81, 54, 72, 4.
г) 7, 490, 700, 20, 300.
д) б, 48, 60, 12, 360.
Задание № 213
Представьте числа 64, 144, 1000 в виде суммы их половин, четвертей и восьмых по образцу: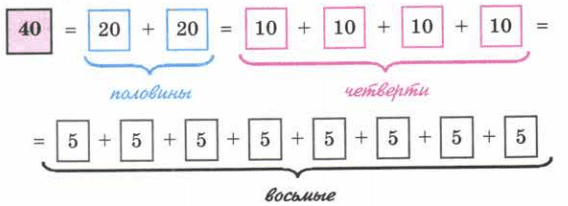
Решение
64 = 32 + 32 = 16 + 16 + 16 + 16 = 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8;
144 = 72 + 72 = 36 + 36 + 36 + 36 = 18 + 18 + 18 + 18 + 18 + 18 + 18 + 18;
1000 = 500 + 500 = 250 + 250 + 250 + 250 = 125 + 125 + 125 + 125 + 125 + 125 + 125 + 125.
Задание № 214
Сколько получится, если:
а) удвоить половину числа а;
б) утроить треть числа х?
Решение
а) $2\ast\frac a2=\frac a2+\frac a2=a$
б) $3\ast\frac{\operatorname х}3=\frac{\operatorname х}3+\frac{\operatorname х}3+\frac{\operatorname х}3=x$
Задание № 215
Восстановите цепочку вычислений:
Решение
a) 1 кг → 250 г → 400 г → 1200 с → 6.
б) 1 ч → 4 мин → 10 мин → 30 с → 6.
Задание № 216
Массы монет выпуска 1961 г. в 1 к., 2 к., 3 к. и 5 к. были равны соответственно 1 г, 2 г, 3 г и 5 г. Какую часть массы пятикопеечной монеты составляет масса каждой из остальных монет? Какую часть массы трёхкопеечной монеты составляет масса каждой из остальных монет?
Монета в 1 коп. составляет 1/5 от массы монеты в 5 коп.
Монета в 2 коп. − 2/5 от массы монеты в 5 коп.
Монета в 3 коп. − 3/5 от массы монеты в 5 коп.
Монета в 1 коп. составляет 1/3 от массы монеты в 3 коп.
Монета в 2 коп. − 2/3 от массы монеты в 3 коп.
Монета в 5 коп. 5/3 от массы монеты в 3 коп.
Задание № 217
За одно сокращение сердце человека выталкивает 150 см3 крови. Сколько крови перекачивает сердце человека за 1 мин, за 1 ч при пульсе 60 (пульс − число сокращений сердца за 1 мин)?
Решение
1) 150 * 60 = 9000 (см3) - крови перекачает сердце за 1 мин
9000 см3 = 9 л
2) 9000 * 60 = 540000 (см3) = 540 (л) - крови перекачает сердце за 1 час
Ответ: 9 л, 540 л.
Задание № 218 с ответами
Выполните действия:
а) $\frac8{25}+\frac7{25}+\frac9{25}=\frac{8+7+9}{25}=\frac{24}{25}$
б) $\frac{13}{15}-(\frac8{15}+\frac4{15})=\frac{13-(8+4)}{15}=\frac1{15}$
в) $(\frac{17}{100}+\frac{27}{100})-(\frac8{100}+\frac3{100})=\frac{17+27}{100}-\frac{8+3}{100}=\frac{44}{100}-\frac{11}{100}=\frac{44-11}{100}=\frac{33}{100}$
г) $(\frac{19}{23}-\frac8{23})+(\frac{16}{23}-\frac{11}{23})=\frac{19-8}{23}+\frac{16-11}{23}=\frac{11}{23}+\frac5{23}=\frac{11+5}{23}=\frac{16}{23}$
Задание № 219
Сколько:
а) граммов в 1/2 кг; в 3/4 кг; в 7/20 кг;
б) минут в 1/2 ч; в 3/4 ч; в 5/6 ч;
в) квадратных метров в 1/2 га; в 1/4 га; в 3/4 га;
г) кубических сантиметров в 1/2м3, в 1/5м3, в 2/5м3?
Решение
Задание № 220
В классе 40 человек. Из них 13 человек ещё не научились плавать. Какая часть учащихся класса умеет плавать?
Решение
40 − 13 = 27 (ч.) - умеют плавать
Это 27 от числа всех учащихся.
40
Ответ: 27.
40
Задание № 221
Кусок джинсовой ткани разрезали на равные части. Из 3 частей сшили брюки, а из 7 остальных частей − куртки. Какую часть материи израсходовали на брюки и какую на куртки?
Решение
3 + 7 = 10 (частей) составляет весь кусок
3 куска израсходовали на брюки
10
7 куска - на куртки
10
Задание № 222
К полднику в детском саду на четырёхместный стол поставили сок, молоко, какао и компот. Сколькими способами четверо детей могут выбрать себе один из напитков?
Решение
Четверо детей могли выбрать напитки 1 * 2 * 3 * 4 = 24 способами.
Задание № 223
По формуле а = bq + r найдите:
а) а, если b = 19, q = 64 и r = 18;
б) b, если а = 567, q = 37 и r = 12;
в) q, если а = 361, b = 25 и r = 11.
Решение
а) при b = 19, q = 64, r = 18;
a = bq + r = 19 • 64 + 18 = 1216 − 1 − 18 = 1234.
б) при a = 567, q = 37, r = 12;
b = (a − r) : q = (567 − 12) : 37 = 555 : 37 = 14.
в) при а = 361, b = 25, r = 11;
q = (a − r) : b = (361 − 11) : 25 = 350 : 25 = 14.
Задание № 224
Решите задачу:
1) Время движения подводной лодки на поверхности воды в 20 раз меньше, чем время движения под водой. Сколько времени подводная лодка находилась под водой, если это время на 57 ч больше, чем время движения на поверхности воды?
2) Подводная лодка прошла под водой путь, в 17 раз больший, чем путь на поверхности воды. Сколько километров прошла лодка под водой, если на поверхности воды она прошла на 320 км меньше, чем под водой?
Решение
1) Время движения на поверхности примем за 1 часть, тогда под водой - 20 частей. Разница между этими частями составляет 57 часов.
1) 57 : 19 = 3 (ч) - лодка находилась на поверхности
2) 3 * 20 = 60 (ч) - лодка находилась под водой
Ответ: 60 ч.
2) Путь на поверхности примем за 1 часть, тогда под водой - 17 частей. Разница между частями составит 320 км.
2) 320 : 16 = 20 (км) - лодка прошла на поверхности воды, а под водой она прошла
17 * 20 = 340 (км) - лодка прошла под водой
Ответ: 360 км.
Решение с помощью уравнений
1) Пусть подводная лодка двигалась на поверхности воды х ч, тогда под водой она находилась 20x ч.
Под водой лодка находилась на (20х − х) ч больше, чем на поверхности.
Составим и решим уравнение:
20х − x = 57
x = 57 : 19
х = 3 (ч)- лодка находилась на поверхности
20 : 3 = 60 (ч) - лодка находилась под водой
Ответ: 60 ч.
2) Пусть подводная лодка прошла на поверхности воды у км , тогда под водой она прошла 17у км.
Под водой лодка прошла на (17у − у) км больше, чем но поверхности.
Составим и решим уравнение:
17у − у = 320
у = 320 : 16
у = 20 (км) - лодка прошла на поверхности воды, а под водой она прошла
17 * 20 = 340 (км) - лодка прошла под водой
Ответ: 360 км.
Задание № 225
Выполните деление с остатком:
1) 2738 на 125;
2) 3049 на 134.
Решение
_2738 |125
250 |21
_238
125
113
_3049 |134
268 |22
_369
268
101
Задание № 226
В углах квадратной площадки установлены одинаковые столбы с четырьмя изоляторами для крепления проводов (рис. 130). Надо протянуть по два провода от столба А к столбу С и от столба В к столбу D так, чтобы провода не касались друг друга. Найдите несколько способов, как это можно сделать.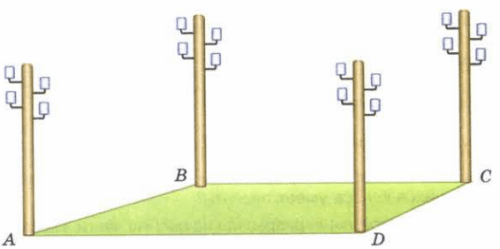
Ответ
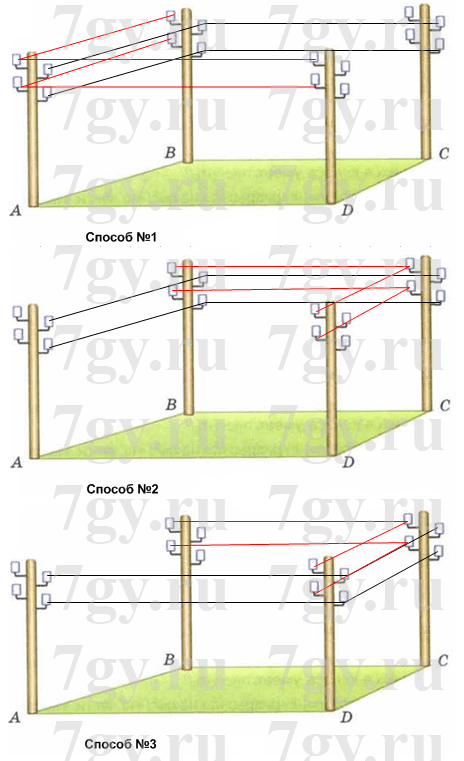
Задание № 227
Запишите в виде дроби частное:
а) 4 : 7;
б) 8 : 11;
в) 1 : 6;
г) 9 : 1.
Решение
а) $4:7=\frac47$
б) $8:11=\frac8{11}$
в) $1:6=\frac16$
г) $9:1=\frac91$
Задание № 228
Запишите дробь в виде частного:
а) 5/9;
б) 18/13;
в) 11/6;
г) 139/100.
Решение
а) $\frac59=5:9$
б) $\frac{18}{13}=18:13$
в) $\frac{11}6=11:6$
г) $\frac{139}{100}=139:100$
Задание № 229
7 м проволоки разрезали на 8 равных кусков. Сколько метров проволоки в одном куске?
Решение
7 : 8 = 7 (м) проволоки
8
Ответ: 7 м проволоки в одном куске.
8
Задание № 230
4 кг варенья разложили в 5 банок поровну. Сколько килограммов варенья в каждой банке?
Решение
4 : 5 = 4 (кг)
5
Ответ: 4 кг варенья в каждой банке.
5
Задание № 231
Две тракторные бригады вспахали вместе 762 га поля. Первая бригада работала 8 дней и вспахивала за день 48 га. Сколько гектаров поля вспахивала за день вторая бригада, если она работала 9 дней? Какая бригада вспахала больше и на сколько?
Решение
1) 8 * 48 = 384 (га) - вспахала первая бригада
2) 762 − 384 = 378 (га) - вспахала вторая бригада
3) 378 : 9 = 42 (га) - вспахивала за день вторая бригада
384 − 378 = 6 (га) - больше вспахала первая бригада, чем вторая.
Ответ: 42 га, на 6 га.
Задание № 232
Расстояние между двумя станциями 784 км. С этих станций одновременно навстречу друг другу вышли два поезда. Они встретились через 8 ч. Найдите скорость каждого поезда, если скорость первого на 10 км/ч больше скорости второго.
Решение
1) 10 * 8 = 80 (км) - на столько обгонит один поезд
2) 784 - 80 = 704 (км) - прошли бы оба поезда с одинаковой скоростью
3) 704 : 2 = 352 (км) - пройдет первый поезд
4) 352 : 8 = 44 (км/ч) - скорость первого поезда
5) 44 + 10 = 54 (км/ч) - скорость второго поезда
Ответ: 44 км/ч, 54 км/ч.
Решение с помощью уравнения
Пусть скорость второго поезда х км/ч, тогда скорость первого поезда (х + 10) км/ч.
Скорость сближения поездов равна (х + х + 10) км/ч, они встретились через 784 : (х + х + 10) ч.
Составим и решим уравнение:
784 : (х + х + 10) = 8
2х + 10 = 784 : 8
х = (98 − 10) : 2
х = 44 (км/ч) − скорость второго поезда
44 + 10 = 54 (км/ч) - скорость первого поезда
Ответ: 44 км/ч, 54 км/ч.
Задание № 233
Выполните деление с остатком:
а) 874 267 на 301;
б) 765 420 на 523.
Решение
а) 874 267 : 301 = 2904 (ост.163)
Проверка: 301 * 2904 + 163 = 874267
б) 765 420 : 523 = 1463 (ост.271)
Проверка: 532 * 1463 + 271 = 765420
Задание № 234
Найдите делимое, если делитель равен 78, неполное частное 96 и остаток 17.
Решение
78 * 96 + 17 = 7488 + 17 = 7505
