Параграф 5. Обыкновенные дроби

Ответы к пункту 22. Окружность и круг, стр. 7

Задание 1

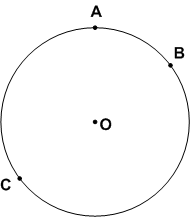
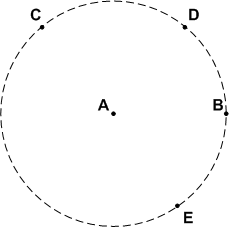
Какие из точек, отмеченных на рисунке 97:
а) лежат на окружности;
б) лежат внутри круга;
в) не лежат на окружности;
г) лежат вне круга?

Решение

а) В, D.

б) А, О, E.

в) А О, Е, С, F.

г) С, F.

Задание 2

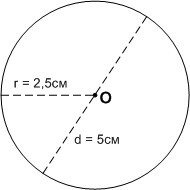
Отметьте в тетради точку О. Постройте окружность с центром в этой точке. Измерьте радиус окружности. Чему равен её диаметр?

Задание 3

Начертите окружность и отметьте на ней три точки А, В и С. Назовите дуги, на которые эти точки делят окружность.

Решение

Точки A, В, С делят окружность на дуги АС, АВ, СВ.

Задание 4

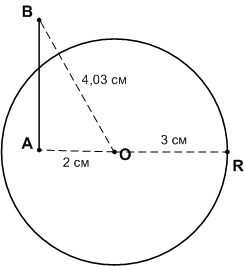
Изобразите круг, радиус которого 3 см. Отметьте точку А внутри круга и точку В вне круга. Измерьте расстояние от центра круга до точки А и до точки В. Сравните эти расстояния с радиусом круга. Соедините точки А и В отрезком. Пересекается ли он с окружностью?

Решение

ОА = 2 см < ОR = 3 см; ОВ = 4,03 см > ОR = 3 см.
Отрезок АВ пересекается с окружностью.

Задание 5

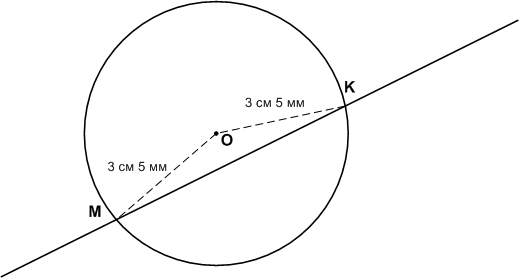
Начертите окружность с центром в точке О и радиусом 3 см 5 мм. Проведите прямую, которая пересекает окружность в точках М и К. На каком расстоянии от центра окружности находятся эти точки?

Решение

ОМ = OK = 3 см 5 мм.

Задание 6

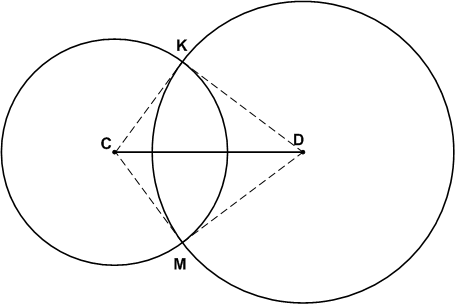
Начертите отрезок CD, равный 5 см. Проведите окружность с центром С и радиусом 3 см, а также другую окружность с центром D и радиусом 4 см. Обозначьте точки пересечения окружностей буквами А и В. Чему равны длины отрезков АС, СВ, DA и BD?

Решение

СK = СM = 3 см, DK = DM = 4 см.

Задание 7

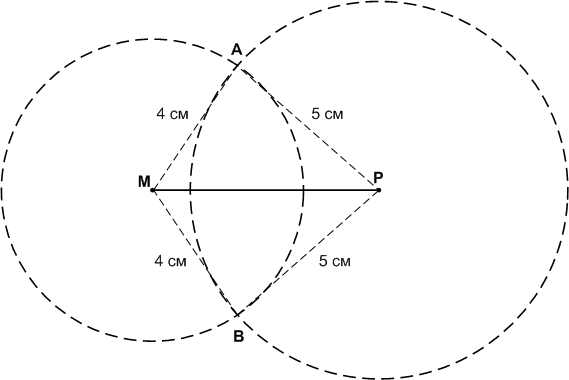
Начертите отрезок MP, равный 6 см. Найдите две точки А и В, которые находились бы на расстоянии 4 см от точки М и 5 см от точки Р.

 

Задание 8

Автомобиль приближается к городу, по улицам которого разрешается ехать со скоростью не более чем 60 км/ч. В кабине автомобиля установлен спидометр − прибор, показывающий скорость движения. Посмотрите на спидометр (рис. 98). Нарушит ли шофёр правила уличного движения, если не снизит скорость? На сколько и в какую сторону передвинется стрелка, когда скорость снизится до 50 км/ч? Каким будет показание спидометра, когда автомобиль остановится?

Решение

На рисунке спидометр показывает скорость 90 км/ч. Значит, если шофёр не снизит скорость, то нарушит правила дорожного движения. При снижении скорости до 50 км/ч, стрелка спидометра передвинется влево на 4 деления. При остановке автомобиля спидометр покажет скорость 0 км/ч.

Задание 9

На рисунке 99 изображена шкала прибора, показывающего, сколько литров бензина осталось в баке автомобиля. Сколько литров бензина сейчас в баке? На сколько делений и в какую сторону передвинется стрелка прибора, если:
а) в бензобак нальют ещё 20 л бензина;
б) при движении будет израсходовано 30 л бензина?

Решение

а) В баке 40 л бензина. Если влить еще 20 л бензина, то стрелка передвинется на 6 делений вправо и покажет 60 л.

б) В баке 40 л бензина. Eсли будет израсходовано 30 л бензина, то стрелка передвинется на 9 делений влево и покажет 10 л.

Задание 10

Какое время показывают часы на рисунке 96? Какое время будут показывать часы, если минутную стрелку передвинуть:
а) назад на 3 больших деления;
б) вперёд на 20 малых делений?

Решение

а) На часах 3 ч 30 мин. Если минутную стрелку передвинуть назад на 3 больших деления, то часы покажут 3 ч 15 мин.

б) На часах 3 ч 30 мин. Если минутную стрелку передвинуть вперёд на 20 маленьких делений, то часы покажут 3 ч 50 мин.

Задание 11

Вычислите устно:

Решение

a) 360, 240, 3, 90.

б) 4, 100, 240, 4.

в) 250, 25, 1000, 700.

г) 70, 140, 350, 7.

д) 400, 8, 1000, 840.

Задание 12

Миллион уменьшили в 100 раз и результат уменьшили на тысячу. Сколько получили?

Решение

1000000 : 100 − 1000 = 10000 − 1000 = 9000.

Задание 13

Укажите координаты точек А, B, С и D, если М(10) (рис. 100). Сравните координаты точек В и С; С и D.

Решение

Одна клетка на рисунке соответствует 2 единицам.
Следовательно координаты других точек: В(6), С(17), A(24), D(28); 6 < 17, 17 < 28.

Задание 14

Сколько сантиметров:
а) в четверти метра;
б) в десятой доле дециметра;
в) в десятой доле метра;
г) в двадцать пятой доле метра?

Решение

a) 1 м = 100 см, 1 дм = 10 cм:
100 см : 4 = 25 см

б) 1 м = 100 см, 1 дм = 10 cм:
100 см : 10 = 10 см

в) 1 м = 100 см, 1 дм = 10 cм:
10 см : 10 = 1

г) 1 м = 100 см, 1 дм = 10 cм:
100 см : 25 = 4 см.

Задание 15

Сколько килограммов:
а) в десятой доле центнера;
б) в сотой доле тонны;
в) в двадцатой доле центнера;
г) в двадцатой доле тонны?

Решение

а) 1 ц = 100 кг, 1 т = 1000 кг:
100 кг : 10 = 10 кг

б) 1 ц = 100 кг, 1 т = 1000 кг:
1000 кг : 100 = 10 кг

в) 1 ц = 100 кг, 1 т = 1000 кг:
100 кг : 20 = 5 кг

г) 1 ц = 100 кг, 1 т = 1000 кг:
1000 кг : 20 = 50 кг

Задание 16

Представьте себе, что один куб с ребром 1 дм разрезали на кубики с ребром 1 см и из этих маленьких кубиков сложили башню, поставив их один на другой. Второй куб с ребром 1 дм разрезали на кубики с ребром 1 мм и из этих кубиков так же сложили башню. Какая из этих башен выше? Во сколько раз?

Решение

Объем куба с ребром 1 дм − V = 1 дм³ = 1000 см³ = 1000000 мм³.
Высота башни из кубиков с ребром 1 см равна 1 * 1000 = 1000 см = 10000 мм, а высота башни из кубиков с ребром 1 мм равна 1 * 1000000 = 1000000 мм.
Поэтому вторая башня выше первой в 1000000 : 10000 = 100 раз.

Задание 17

Проверьте, справедливы ли равенства:
1³ + 2³ = ( 1 + 2 )² ;
1³ + 2³ + 3³ = ( 1 + 2 + 3 )² ;
1³ + 2³ + 3³ + 4³ = ( 1 + 2 + 3 + 4 )² .
Попробуйте рассказать, какова в этих равенствах зависимость между квадратами и кубами чисел. Проверьте, выполняется ли это свойство для пяти, шести чисел.

Решение

1³ + 2³ = 1 + 8 = 9 ,
( 1 + 2 )² = 3² = 9 ;

1³ + 2³ + 3³ = 1 + 8 + 27 = 36 ,
( 1 + 2 + 3 )² = 6² = 36 ;

1³ + 2³ + 3³ + 4³ = 1 + 8 + 27 + 64 = 100 ,
( 1 + 2 + 3 + 4 )² = 10² = 100

Сумма кубов n первых натуральных чисел равна квадрату суммы этих чисел.

1³ + 2³ + 3³ + 4³ + 5³= 1 + 8 + 27 + 64 + 125 = 225 ,
( 1 + 2 + 3 + 4 + 5)² = 15² = 225

1³ + 2³ + 3³ + 4³ + 5³ + 6³= 1 + 8 + 27 + 64 + 125 + 216 = 441 ,
( 1 + 2 + 3 + 4 + 5 + 6 )² = 21² = 441

Задание 18

Найдите объём и площадь наружной поверхности бака без крышки, изображённого на рисунке 101. Сколько понадобится краски, чтобы покрасить этот бак снаружи и изнутри, если на покраску 1 дм² нужно 2 г краски? Сколько литров бензина можно влить в этот бак?

Решение

V бака = 80 * 90 * 70 = 504000 (см³ ).
S наружн.поверхности = 90 * 70 + 2 * ( 80 * 90 + 80 * 70 ) = 6300 + 2 * 12800 = 31900 (см² )
31900 * 2 : 100 * 2 = 1276 (г) краски потребуется  на покраску бака.
504000 : 1000 = 504 (л) - бензина можно влить в бак

Задание 19

Сторона одного куба 9 см, а другого 5 см; На сколько объём первого куба больше объёма второго? На сколько площадь поверхности первого куба больше площади поверхности второго?

Решение

1) 9³ − 5³ = 729 − 125 = 604 (см³ ) - на столько объем первого куба больше объёма второго куба.
2) ( 9² − 5² ) = 6 * 56 = 336 (см² ) - на столько площадь поверхности первого куба больше.

Задание 20

Найдите площадь фигуры, изображённой на рисунке 102. Площадь одной клетки 25 мм².

Решение

1) 7 + 2 * 5 = 17 (клеток) - в фигуре
2) 17 * 25 = 425 (мм²) - площадь фигуры
Ответ: 425 мм².

Задание 21

На одной чашке весов стоит банка с вареньем, а на другой − гиря в 1 кг. Весы находятся в равновесии. Сколько граммов варенья находится в банке, если пустая банка легче варенья в 4 раза?

Решение от

Пусть пустая банка весит х г, тогда варенье весит 4х г.
Общая масса банки с вареньем равна (х + 4х) г.
Составим и решим уравнение:
х + 4х = 1000
5x = 1000
х = 1000 : 5
х = 200 (г) - весит пустая банка
4 * 200 = 800 (г) - весит варенье
Ответ: 800 г  варенья находится в банке.

Задание 22

Решите задачу:
1) На крыше дома сидели голуби. Когда к ним прилетели ещё 15 голубей, а 18 голубей улетели, то на крыше оказалось 16 голубей. Сколько голубей сидело на крыше первоначально?
2) Когда от товарного состава отцепили 6 вагонов, а прицепили к нему 19 вагонов, в нём стало 50 вагонов. Сколько вагонов было в составе первоначально?

Решение задач

1) Пусть на крыше сидели х голубей, тогда на ней стало (х + 15 − 18) голубей.
Составим и решим уравнение:
х + 15 − 18 = 16
х = 16 + 3
х = 19 (г.)
Ответ: 19 голубей сидело на крыше первоначально.

2) Пусть в составе было х вагонов, тогда в составе стало (z − 6 + 19) вагонов.
Составим и решим уравнение:
z − 6 + 19 = 50
z = 50 − 13
z = 37 (в.)
Ответ: 37 вагонов было в составе первоначально.

!Задание 23

Выполните действия:
1) (1 445 561 : 3587 − 208) * 356 − 3580;
2) (1 420 288 : 4672 + 259) * 234 − 1742.

Решение

1) (1445561 : 3587 − 208) * 356 + 3580 = (403 − 208) * 356 + 3580 = 69420 − 3580 = 65840

2) (1420288 : 4672 + 259) * 234 − 1742 = (304 + 259) * 234 − 1742 = 131742 − 1742 = 130000

Задание 24

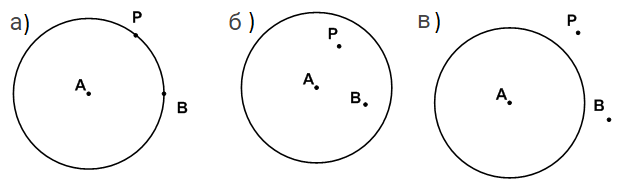
Начертите круг с центром А и радиусом 2 см. Отметьте две точки:
а) лежащие на окружности;
б) лежащие внутри круга;
в) лежащие вне круга.

Страница 12

Задание 25

Отметьте две точки А и В так, чтобы АВ = 3 см. С помощью циркуля постройте ещё три точки С, D и Е, которые находились бы от точки А на расстоянии 3 см.

Задание 26

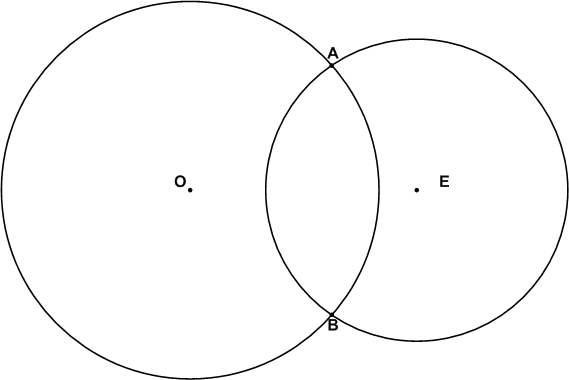
Отметьте две точки К и Р так, чтобы КР = 6 см. Постройте окружность с центром К и радиусом 5 см и окружность с центром Р и радиусом 4 см. Пересекаются ли эти окружности?

Решение

Окружности пересекаются в точках А и B.

Задание 27

Отметьте точки О и Е так, чтобы ОЕ = 8 см. Постройте окружность с центром О и радиусом 2 см и окружность с центром Е и радиусом 4 см. Пересекаются ли эти окружности?

Решение

Окружности не пересекаются.

Задание 28

В старину часто пользовались солнечными часами, они известны более 3000 лет. В солнечных часах время определяется по положению тени от наклонного стержня на циферблате (циферблат и стержень располагали так, чтобы в полдень тень от стержня была направлена на отметку 12 ч). подумайте, что общего у солнечных часов (рис. 103) с современными, в чём их достоинства и недостатки.

Решение

Солнечные и современные часы показывают время, их достоинство в том, что они не требуют энергии для своей работы, а недостаток в том, что они не показывают время ночью и ими неудобно пользоваться.

Задание 29

Решите уравнение:
а) (х − 152) * 59 = 6018;
б) 975 * (у − 361) = 14 625;
в) (30 142 + z) : 876 = 49;
г) 51 815 : (р − 975) = 1205;
д) 13х + 15x − 24 = 60;
е) 18у − 7у − 10 = 12.

Решение

а) (х − 152) * 59 = 6018
x − 152 = 6018 : 59
x = 102 + 152
х = 254
Ответ: 254.

б) 975 * (у − 361) = 14625
у − 361 = 14625 : 975
у = 15 + 361
у = 376
Ответ: 376.

в) (30142 + z) : 876 = 49
30142 + z = 49 * 876
z = 42924 − 30142
z = 12782
Ответ: 12782.

г) 51815 : (р − 975) = 1205
р − 975 = 51815 : 1205
р = 43 + 975
р = 1018
Ответ: 1018.

д) 13х + 15x − 24 = 60
28х = 60 + 24
х = 84 : 28
х = 3
Ответ: 3.

е) 18у − 7у − 10 = 12
11у = 12 + 10
у = 22 : 11
у = 2
Ответ: 2.

Задание 30

Выполните деление с остатком числа 987654 на 391.

Решение

_987654 |391   
  782       |2525
_2056
  1955
  _1015
      782
    _2334
      1955
        379
987654 = 2525 * 391 + 379.

Задание 31

Найдите объём фигуры, изображённой на рисунке 12. Объём каждого кубика 1 см³.

Решение

а) 2 * 2 * 5 = 20 (см³ )
Ответ: объем фигуры 20 см³ .

б) 10 * 10 * 10 = 1000 (см³ )
Ответ: объем фигуры 1000 см³ .

в) 10 * 10 * 5 = 500 (см³)
Ответ: объем фигуры 500 см³ .

Задание 32

Масса 1 л бензина 650 г. В бензобак автомобиля входит 95 л бензина. Какова масса бензина в полном баке этой автомашины?

Решение

95 * 650 = 61750 (г)  -  масса бензина в бензобаке.
61750 г = 61 кг 750 г
Ответ: 61 кг 750 г.

Задание 33

По формуле а = bq + r найдите число а, если делитель b равен 81, неполное частное q равно 561 и остаток r равен 23.

Решение

Если b = 81, q = 561, r = 23;
a = bq + r = 81 * 561 + 23 = 45441 + 23 = 45464.

!Задание 34

Найдите значение выражения:
а) 507 * 664 − 296 085;
б) 485 979 + 691 * 308;
в) 12³ + 5³ * 4 ;
г) ( 10³ + 8³ ) : 18 .

Решение

а) 507 * 664 − 296085 = 336648 − 296085 = 40563

б) 485979 + 691 * 308 = 485979 + 212828 = 698807

в) 12³ + 5³ * 4 = 144 * 12 + 125 * 4 = 1728 + 500 = 2228

г) ( 10³ + 8³ ) : 8 = ( 1000 + 512 ) : 18 = 1512 : 18 = 84