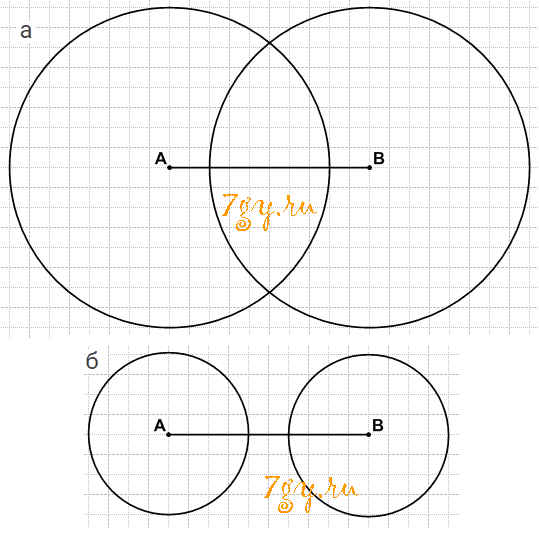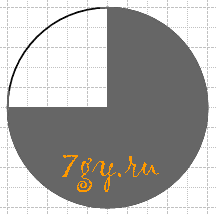Ответы к пункту 23. Доли. Обыкновенные дроби, стр. 13

Задание 35

Начертите в тетради квадрат со стороной в 6 клеток. Разделите его на три доли. Начертите отдельно треть квадрата.

Задание 36

Разделите тремя способами квадрат со стороной 4 см на 4 доли. Начертите четверть квадрата, половину квадрата.

Задание 37

Какая часть фигуры закрашена (рис. 109)?

Решение

а) закрашена 1/7 часть отрезка 

б) закрашена 1/3 часть квадрата 

в) закрашена 1/4 часть круга 

г) закрашена 1/2 часть треугольника 

д) закрашено 2/5 части прямоугольника 

е) закрашено 2/5 части круга 

ж) закрашено 1/3 части треугольника 

з) закрашено 5/6 части прямоугольника 

и) закрашено 4/10 части квадрата 

к) закрашено 5/5 частей круга 

л) закрашена 1/2 часть квадрата 

м) закрашено 3/5 части прямоугольника 

н) закрашено 7/8 частей круга 

o) закрашено 8/100 частей квадрата

Задание 38

Как называется:
а) одна сотая доля метра;
б) одна тысячная доля тонны;
в) одна двадцать четвёртая доля суток;
г) одна шестидесятая доля часа;
д) одна миллионная доля квадратного метра;
е) одна миллионная доля кубического метра?

Решение

a) 1 см

б) 1 кг

в) 1 ч

г) 1 мин

д) 1 мм

е) 1 см³

Задание 39

Прочитайте записи: 1/7 отрезка, 1/100 кг, 1/12 суток, 1/3 дороги, 1/4 дыни, 1/2 яблока.

Решение

Одна седьмая часть отрезка, одна сотая часть килограмма, одна двенадцатая часть суток, одна третья часть дороги, одна четвёртая часть дыни, одна вторая часть яблока.

Задание 40

Купили кусок ткани длиной 2 м 50 см и из 1/5 куска сшили платье для куклы. Сколько сантиметров ткани ушло на это платье?

Решение

250 * $\frac15$ = 50 (см) -  ткани ушло на платье.
Ответ: 50 см.

 

Задание 41

Купили дыню массой 2 кг 400 г. Ване отрезали 1/5 дыни, а Маше − 1/6 дыни. Чему равна масса каждого отрезанного куска? Сколько граммов дыни осталось?

Решение

1) 2400 * $\frac15$ = 480 (г) -  дыни отрезали Ване. 
2) 2400 * $\frac16$ = 400 (г) -  дыни отрезали Маше.
3) 2400 − (480 + 400) = 2400 − 880 = 1520 (г) - дыни осталось.
Ответ: 480 г, 400 г, 1520 г.

Задание 42

Петя готовил уроки 1 ч 40 мин. На математику он потратил 1/5 этого времени, а на историю − 1/4 оставшегося времени. Сколько минут Петя готовил уроки по математике и сколько по истории?

Решение

 
1) 100 * $\frac15$ = 20 (мин) - потратил Петя на математику.
2) (100 − 20) * $\frac14$ = 80 * 1/4 = 20 (мин) - потратил Петя на историю.
Ответ: по 20 минут.

Задание 43

Начертите квадрат со стороной 6 клеток. Разделите его на 3 доли и закрасьте 2/3 квадрата. Какая часть квадрата осталась незакрашенной?

Решение

Не закрашенной осталась 1/3 часть квадрата.

Задание 44

Начертите отрезок длиной 8 см. Отметьте цветным карандашом 5/8 отрезка. Какая часть отрезка осталась неотмеченной?

Решение

Не отмеченными остались 3/8.

Задание 45

Прочитайте дроби: 2/7 , 3/4 , 9/10 , 6/12 , 3/1000 , 5/247 , 7/90000 .
Назовите числитель и знаменатель каждой дроби.

Решение

2/7 − две седьмых,
3/4 − три четвертых,
9/10 − девять десятых,
6/12 − шесть двенадцатых,
3/1000 − три тысячных,
5/247 − пять двести сорок седьмых,
7/90000 − семь девяносто тысячных.
Числитель вверху, знаменатель внизу.

Задание 46

Запишите в виде обыкновенной дроби:
а) три шестых;
б) одна треть;
в) половина;
г) три четверти;
д) семь десятых;
е) одиннадцать сотых;
ж) одиннадцать сорок восьмых.

Решение

а) $\frac36$

б) $\frac13$

в) $\frac12$

д) $\frac34$

е) $\frac{11}{100}$

ж) $\frac{11}{48}$

Задание 47

Дорога от Фабричного до Ильинского равна 8 км (рис. 110). Лена прошла по этой дороге 3 км. Какую часть дороги она прошла?

Решение

Длина всей дороги равна 8 км.
Поэтому 1 км составляет 1/8 всей дороги, а 3 км - 3/8 дороги.
Значит, Лена прошла 3/8 дороги.

Задание 48

В январе 31 день, а в году 365 дней. Какую часть года составляет январь? апрель? февраль?

Решение

Один день − $\frac{1}{365}$ часть года.

В январе 31 день,поэтом у он составляет $\frac{31}{365}$ года.

В апреле 30 дней − $\frac{30}{365}$ года.

В феврале 28 дней − $\frac{28}{365}$ года.

Задание 49

В январе 1995 года с 1 января по 10 января были зимние каникулы, 15, 22 и 29 января были воскресными днями, а остальные − учебными. Какую часть января составили свободные от учёбы дни? Какую часть составили учебные дни?

Решение от

В январе 31 день, поэтому 1 день составляет $\frac{1}{31}$ часть января.

Свободным от учебы в январе были 13 дней, что составляет $\frac{13}{31}$ часть месяца.

Учебных дней в январе было 31 − 13 = 18, что составляет − $\frac{18}{31}$ часть месяца.

Задание 50

Площадь поля 16 км². Пшеницей засеяли 11 км², рожью − 5 км². Какая часть поля засеяна пшеницей и какая рожью?

Решение

По условию 1 км² составляет 1/16 часть поля, следовательно пшеницей засеяно 11/16 поля, а рожью 5/16 поля.

Задание 51

Дорога от Фабричного до Отдыха составляет 3/4 дороги от Фабричного до Ильинского. Чему равно расстояние от Фабричного до Отдыха, если от Фабричного до Ильинского 8 км?

Решение

Разделим всю дорогу на 4 доли (рис. 111).
Тогда длина одной доли дороги равна 8 : 4, то есть 2 км.
А длина 3/4 дороги, то есть трёх таких долей, равна 2 * 3, то есть 6 км.
Значит, от Фабричного до Отдыха 6 км.

Задание 52

Длина дороги 20 км. Заасфальтировали 2/5 дороги. Сколько километров дороги заасфальтировали? Сколько осталось заасфальтировать?

Решение

Длина одной пятой дороги равна 20 : 5 = 4 км, следовательно 2/5 дороги составляют 2 * 4 = 8 км, и осталось заасфальтировать 20 − 8 = 12 км.

Задание 53. На базу в Антарктиду доставили 22 собаки. Из 5/11 всех собак составили упряжку, на которой отправились в поход. Сколько собак не вошло в упряжку?

Решение

1) 22 : 11 * 5 = 10 (с.) -  вошли в упряжку.
2) 22 − 10 = 12 (с.) - не вошло в упряжку.
Ответ: 12 собак не вошло в упряжку.

Задание 54. Купили 5 кг 600 г сахара и израсходовали на варенье 7/8 всего сахара. Сколько сахара пошло на варенье? Сколько сахара осталось?

Решение

1) 5600 : 8 * 7 = 4900 (г) - израсходовали на варенье.
4900 г = 4 кг 900 г
2) 5600 − 4900 = 700 (г) - сахара осталось.
Ответ: 4900 г сахара израсходовали на варенье, 700 г осталось.

Задание 55

Сколько молока в бидоне, если 1/5 этого молока составляет 13 л?

Решение

Всего в бидоне в пять раз больше, то есть
13 * 5 = 65 (л)  молока.

Задание 56

Дорога от Фабричного до Кратова равна 5 км, что составляет 5/8 дороги от Фабричного до Ильинского. Найдите расстояние от Фабричного до Ильинского.

Решение

Так как пять восьмых дороги составляют 5 км, то одыа восьмая этой дороги равна 5 : 5, то есть 1 км. А тогда вся дорога в 8 раз длиннее, чем 1 км, то есть имеет длину 1 * 8, или 8 км.
Итак, от Фабричного до Ильинского 8 км.

 

Задание 57

Человек прошёл 2/3 дороги. Какова длина всей дороги, если он прошёл 4 км?

Решение

4 : 2 * 3 = 6 (км)
Ответ: длина всей дороги 6 км.

Задание 58

Велосипедист проехал 2/9 дороги. Какова длина дороги, если он проехал 40 км?

Решение

Из условий задачи следует что 2/9 пути равны 40 км, значит 1/9 пути равна 40 : 2 = 20 км, а длина всего пути 20 * 9 = 180 км.

40 : 2 9 = 180 (км)
Ответ: длина дороги 180 км.

Задание 59

Миша исписал 10 страниц тетради, что составляет 5/6 всей тетради. Сколько страниц в тетради?

Решение

Из условий задачи следует что 5/6 тетради составляют 10 страниц, значит 1/6 тетради составляют 10 : 5 = 2 страницы, а всего в тетради 2 * 6 = 12 страниц.

10 : 5 * 6 = 12 (стр.)
Ответ? в тетради 12 страниц.

Задание 60

В куске материи 96 м. Для детского сада взяли 3/8 этого куска, а для детских яслей 5/12 куска. Для кого взяли больше материи − для детского сада или для яслей? На сколько метров?

Решение

1) 96 : 8 * 3 = 12 * 3 = 36 (м) - материи взяли для детского сада. 
2) 96 : 12 * 5 = 8 * 5 = 40 (м) - материи для яслей.
3) 40 − 36 = 4 (м) - материи больше взяли для яслей.
Ответ: на 4 м материи больше взяли для яслей.

Задание 61

Вычислите устно:

Решение

a) 810, 9, 450, 600.

б) 10, 300, 550, 11.

в) 630, 9, 360, 500.

г) 8, 1000, 5, 600.

Задание 62

Десятую часть миллиона уменьшили на 10 000 и результат уменьшили в тысячу раз. Сколько получили?

Решение

(1000000 : 10 − 10000) : 1000 = (100000 − 10000) : 1000 = 90000 : 1000 = 90.

Задание 63. Имеется круг, диаметр которого 10 см. Найдутся ли две точки этого круга, расстояние между которыми: 5 см; 1 см; 10 см; 12 см? Ответьте на те же вопросы для окружности радиусом 5 см.

Решение

Максимальное расстояние между точками круга не превышает длину диаметра этого круга, следовательно у круга с диаметром 10 см есть точки, между которыми 5 см, 1 см, 10 см, но не существует точек между которыми расстояние 12 см. Круг радиусом 5 см это то же самое, что и круг диаметром 10 см.

Задание 64

Приведите примеры предметов, имеющих форму окружности; круга; дуги окружности; полукруга.

Решение

Окружность: обруч, кольцо.
Круг: тарелка, крышка, колесо.
Дуга окружности: лезвие серпа; ободок; подкова.
Полукруг: арбузная долька, полумесяц.

Задание 65

Поставьте вместо многоточия необходимые слова: ««Отрезок называется диаметром, если он ... и он ...»

Решение

Отрезок называется диаметром, если он соединяет 2 точки окружности и он проходит через ее центр.

Задание 66

Сколько минут:
а) в трети часа;
б) в четверти часа;
в) в половине часа;
г) в десятой доле часа;
д) в двенадцатой доле часа;
е) в шестой доле половины часа?

Решение

а) $\frac13$ ч = 60 : 3 = 20 мин

б) $\frac14$ ч = 60 : 4 = 15 мин

в) $\frac12$ ч = 60 : 2 = 30 мин

г) $\frac1{10}$ ч = 60 : 10 = 6 мин

д) $\frac1{12}$ ч = 60 : 12 = 5 мин

е) $\frac16$ от $\frac12$ ч = 30 : 6 = 5 мин

Задание 67

Сколько секунд:
а) в 5 минутах;
б) в четверти часа;
в) в одном часе;
г) в четверти минуты;
д) в трети минуты;
е) в половине минуты?

Решение

a) 5 мин = 5 * 60 = 300 с

б) $\frac14$ ч = 60 * 60 : 4 = 900 с

в) 1 ч = 60 * 60 = 3600 с

г) $\frac14$ мин = 60 : 4 = 15 с

д) $\frac13$ мин = 60 : 3 = 20 с

е) $\frac12$ мин = 60 : 2 = 30 с

 

Задание 68

Сколько в действительности времени, если часы, отражённые в зеркале (рис. 113), показывают 9 ч; 8 ч; 6 ч 15 мин; 10 ч 40 мин? Когда часы и их отражение покажут одинаковое время?

Решение

Показания часов в зеркале и их показания в действительности симметричны относительно вертикальной оси проходящей через цифры 6 и 12. Поэтому 9 ч в зеркале − 3 ч в действительности, 8 ч − 4 ч, 6 ч 15 мин − 5 ч 45 мин, 10 ч 40 мин − 1 ч 20 мин. Одинаковое время на часах будет когда минутная и часовая стрелки находятся одновременно на вертикальной оси, то есть в 12 ч и 6 ч.

Задание 69. Отметьте точки А и В так, что АВ = 5 см. Проведите окружности одинакового радиуса с центрами А и B так, чтобы они:
а) пересекались в двух точках;
б) не имели общих точек.

Задание 70

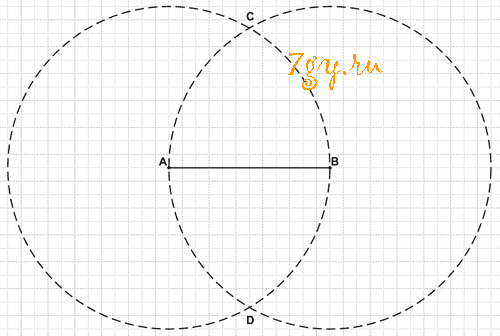
Начертите отрезок АВ = 6 см. Найдите точки, которые удалены от А и от В на 6 см.

Решение

Точки C и D удалены от А и от В на 6 см.

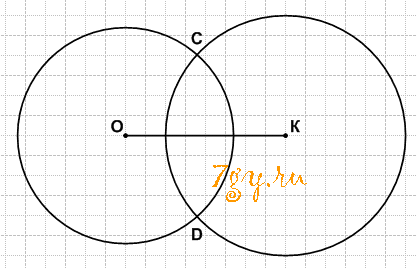
Задание 71. Начертите окружность с центром в точке О и радиусом 2 см 6 мм (рис. 114). Отметьте такую точку К, чтобы ОК = 4 см. Найдите с помощью циркуля на окружности точки, удалённые от точки К на 3 см.

Решение

Точки С и D удалены от точки K на 3 см.

Задание 72

 

Бетонный блок имеет длину 12 дм, ширину 8 дм и высоту 5 дм. Из таких блоков сложили стену длиной 240 дм, шириной 24 дм и высотой 30 дм. Сколько блоков потребовалось для этого?

Решение

1) 12 * 8 * 5 = 480 (дм³) - объем одного блока.
2) 240 * 24 − 30 = 172800 (дм³) - объем стены.
3) 172 800 : 480 = 360 (б.) - потребовалось
Ответ: на строительство стены потребовалось 360 блоков.

Задание 73

На книжную полку ставят 6 разных книг. Сколькими способами эти книги можно разместить на полке?

Решение

6! = 1 * 2 * 3 * 4 * 5 * 6 = 720 (способами)

Задание 74

Решите задачу:
1) В двух спортивных секциях поровну участников. Если в каждую из них войдут ещё по 2 участника, то всего в них будет 36 человек. Сколько человек занимается в каждой секции?
2) В трёх классах поровну учащихся. Если в каждый класс добавить ещё по 3 учащихся, то всего в них будет 129 учащихся. Сколько человек учится в каждом классе?

Решение

1) Пусть в каждой секции занимается х человек, тогда после пополнения всего будут
заниматься 2 * (х + 2) человека.
Составим и решим уравнение:
2(х + 2) = 36
х + 2 = 36 : 2 = 18
х = 18 − 2
х = 16 (ч.)
Ответ: по 16 человек занимается в каждой секции.

2) Пусть в каждом классе х учащихся, тогда в каждом классе станет (x + 3) учащихся.
Общее число учащихся будет 3 * (х + 3) человека.
Составим и решим уравнение:
3 * (х + 3) = 129
у + 3 = 129 : 3 = 43
у = 43 − 3
у = 40 (уч.)
Ответ: по 40 учащихся в каждом классе.

!Задание 75

Выполните действия:
1) 90 720 : (207 : 23 * 840);
2) 22 624 : 56 * (816 : 8);
3) 14 700 : 21 : 7 * 49;
4) 140 : 10 : (49 : 7) : (10 : 5).

Решение

1) 90720 : (207 : 23 * 840) = 90720 : (9 * 840) = 90720 : 7560 = 12

2) 22624 : 56 * (816 : 8) = 404 * 102 = 41208

3) 14700 : 21 : 7 − 49 = 700 : 7 − 49 = 100 * 49 = 4900

4) 140 : 10 : (49 : 7) : (10 : 5) = 14 : 7 : 2 = 2 : 2 = 1

Задание 76. Начертите круг радиусом 2 см и закрасьте 3/4 круга.

Задание 77

Из трёхлитрового бидона с молоком взяли 2 л молока. Какую часть всего молока взяли?

Решение

1 л молока составляет 1/3 часть бидона, следовательно всего взяли 2/3 молока.

Задание 78

Площадь квадрата 16 см². Найдите, чему равна площадь:
а) 3/4 квадрата;
б) половины квадрата.

Решение

a) 16:4*3 = 4*3 = 12 (см²)

б) 16:2 = 8 (см²)

Задание 79

На огороде собрали 42 кг огурцов и 5/7 всех огурцов засолили. Сколько килограммов огурцов засолили?

Решение

1/7 часть огурцов равна 42 : 7 = 6 кг, значит засолили 5 * 6 = 30 кг огурцов.

42 : 7 * 5 = 30 (кг) - огурцов засолили.
Ответ: 30 кг огурцов.

 

Задание 80

Мастерская получила 700 м шёлка. Из 2/7 полученной ткани сшили блузки, а из 2/5 полученной ткани сшили платья. Сколько метров шёлка осталось?

Решение

1) 700 : 7 * 2 = 100 * 2 = 200 (м) - ткани пошло на блузки,
2) 700 : 5 * 2 = 140 * 2 = 280 (м) - ткани пошло на платья.
3) 700 − (200 + 280) = 700 − 480 = 220 (м) - ткани осталось.
Ответ: 220 м шёлка осталось.

Задание 81

До перерыва шахматисты играли 4/5 всего времени партии. Сколько времени продолжалась партия, если до перерыва шахматисты играли 2 ч?

Решение

1) 120 м : 4 = 30 мин - 1/5 часть времени партии.
2) 30 * 5 = 150 мин = 2 ч 30 мин продолжалась партия.
Ответ: партия продолжалась 2 ч 30 мин.

Задание 882

До обеда выгрузили 7/10 зерна, находившегося в товарном вагоне. Сколько тонн зерна было в вагоне, если выгрузили 42 т?

Решение

42 : 7 * 10 = 60 (т) - зерна было в вагоне.
Ответ: 6 т.

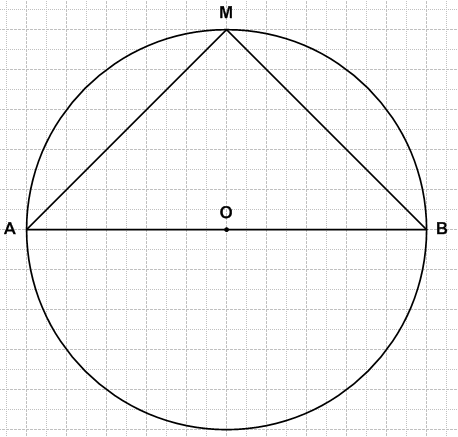
Задание 83

Постройте круг радиусом 5 см. Проведите в нём диаметр АВ. Отметьте на окружности точку М и соедините её с точками А и В. Измерьте: диаметр АВ, отрезок АМ, отрезок MB. Какой из этих отрезков самый длинный?

Решение

AB = 10 см − самый длинный
AM = MB = 7 см 7 мм

Задание 84

Какую часть 1 м³ составляет 1 см³? Какую часть 1 м² составляет 1 см²?

Решение

1) $1{\operatorname м}^3=1000000{\operatorname с}{\operatorname м}^3,1{\operatorname с}{\operatorname м}^3=\frac1{1000000}{\operatorname м}^3$
2) $1{\operatorname м}^2=10000{\operatorname с}{\operatorname м}^2,1{\operatorname с}{\operatorname м}^2=\frac1{10000}{\operatorname м}^2$

Задание 85

Найдите значение выражения:
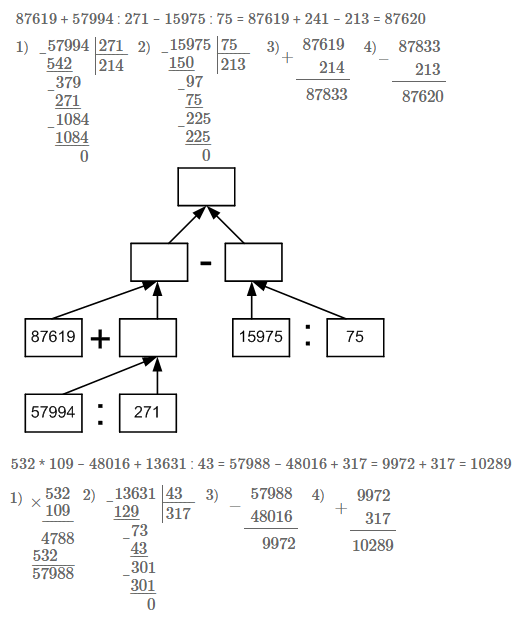
а) 87619 + 57994 : 271 − 15975 : 75;
б) 532 * 109 − 48016 + 13631 : 43.
Для выражения а) составьте программу и схему вычисления.

Решение

а) 1) Делим 57994 на 271;
2) Делим 15975 на 75;
3) 87619 + результат 1 действия;
4) Результат 3 действия − результат 2 действия.

Задание 86

Разгадайте кроссворд, помещённый на форзаце в конце учебника.

Решение

По горизонтали:
1. Двести. 3. Вершок. 8. Секунда. 9. Деление. 10. Уравнение. 14. Дециметр.
По вертикали:
2. Игрек. 4. Штрих. 5. Баррель. 6. Фунт. 7. Единица. 11. Мера. 12. Литр. 13. Промилле.

Задание 87

Иван Иванович отправился из дому на рыбную ловлю. Три часа он ехал поездом со скоростью 75 км/ч. Потом а ч он шёл пешком со скоростью 5 км/ч, наконец, 2 ч плыл на лодке по озеру со скоростью v км/ч. Какой путь проделал Иван Иванович от вокзала до места рыбалки? Найдите значение получившегося выражения, если:
а) а = 3, v = 6;
б) а = 4, v = 10.

Решение

а) Составим и упростим выражение 3 * 75 + а * 5 + 2 * v = 225 + 5а + 2v (км)
При а = 3 и v = 6
225 + 5а + 2v = 225 + 5 * 3 + 2 * 6 = 225 + 15 + 12 = 252 (км)

б) Составим и упростим выражение 3 * 75 + а * 5 + 2 * v = 225 + 5а + 2v (км)
При а = 4 и v = 10
225 + 5а + 2v = 225 + 5 * 4 + 2 * 10 = 225 + 20 + 20 = 265 (км)

Задание 88

Мотоциклист и велосипедист едут навстречу друг другу. Через сколько часов они встретятся, если расстояние между ними 272 км, скорость велосипедиста 12 км/ч, а скорость мотоциклиста 56 км/ч?

Решение

272 : (12 + 56) = 272 : 68 = 4 (ч)
Ответ: мотоциклист и велосипедист встретятся через 4 часа.

Задание 89

По рисунку 115 найдите площади треугольников ABC, ACD, ABO и ВСО.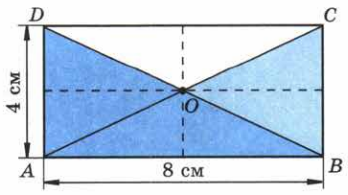

Решение

S ABCD = AB * AD = 8 * 4 = 32 см²;
S ABC = S ABCD : 2 = 30 : 2 = 16 см²;
S ACD = S ABC = 16 см²,
S ABO = S ABCD : 4 = 32 : 4 = 8 см²,
S ВСО = S ABCD : 4 = 32 : 4 = 8 см².

Задание 90

У продавца 80 кг яблок. Первый покупатель приобрёл 10 кг яблок, а остальные а покупателей − по 6 кг каждый. Сколько яблок осталось у продавца? Какие значения может принимать а?

Решение

У продавца осталось 80 − (10 + 6 * а) = 70 − 6а (кг) яблок.
В полученном выражении а может принимать натуральные значения от 0 до 11.