Пункт 33. Приближенные значения чисел. Округление чисел. Страница 81

Задание 420

Между какими соседними натуральными числами расположена каждая из дробей: 6,78; 83,74; 126,2? К какому из этих чисел дробь ближе?

Решение

6 < 6,78 < 7;
дробь 6,78 расположена ближе к числу 7; 83 < 83,74 < 84;
дробь 83,74 расположена ближе к числу 84; 126 < 126,2 < 127;
дробь 126,2 расположена ближе к числу 126.

Задание 421

Длина прямоугольника х см, а его ширина у см. Укажите приближённые значения с недостатком и с избытком для периметра и для площади этого прямоугольника, если:
а) 7 < х < 8, 3 < у < 4;
б) 20 < х < 25, 16 < у < 18.

Решение

а) P = 2(a + b), S = ab, где а − длина, b − ширина прямоугольника:
при 7 < x < 8, 3 < y < 4,
то 2 * (7 + 3) < Р < 2 * (8 + 4) => 20 < Р < 24;
7 * 3 < S < 8 * 4 => 21 < S < 32.

б) P = 2(a + b), S = ab, где а − длина, b − ширина прямоугольника:
при 20 < х < 25, 16 < у < 18,
то 2 * (20 + 16) < Р < 2 * (25 + 18) => 72 < Р < 86,
20 * 16 < 5 < 25 * 18 => 320 < S < 450.

Задание 422

Округлите до единиц дроби:
7,265; 11,638; 0,23; 8,5; 300,499; 6,5108; 0,8.

Решение

7,265 ≈ 7
11,638 ≈ 12
0,23 ≈ 0
8,5 ≈ 9
300,499 ≈ 300
6,5108 ≈ 7
0,8 ≈ 1

Задание 423

Старинная русская мера массы пуд равна 16,38 кг. Округлите это значение до целых, до десятых. Старинная русская мера длины верста равна 1067 м. Округлите это значение до десятков, до сотен. Старинная русская мера длины сажень равна 2,13 м. Округлите это значение до целых, до десятых.

Решение

1 пуд = 16,38 кг ≈ 16 кг, 16,38 кг ≈ 16,4 кг;
1 верста = 1067 м ≈ 1070 м; 1067 м ≈ 1100 м;
1 сажень = 2,13 м ≈ 2 м, 2,13 м ≈ 2,1 м.

Задание 424

Округлите дроби:
а) 2,781; 3,1423; 203,962; 80,46 до десятых;
б) 0,07268; 1,35506; 10,081; 76,544; 4,455 до сотых;
в) 167,1; 2085,04; 444,4; 300,7; 137 до десятков.

Решение

а) 2,781 ≈ 2,8
3,1423 ≈ 3,1
203,962 ≈ 204,0
80,46 ≈ 80,5

б) 0,07268 ≈ 0,07
1,35506 ≈ 1,36
10,081 ≈ 10,08
76,544 ≈ 76,54
4,455 ≈ 4,46

в) 167,1 ≈ 170
2085,04 ≈ 2090
444,4 ≈ 440
300,7 ≈ 300
137 ≈ 140

Задание 425

Одна деталь имеет массу 13,26 кг, вторая − 14,43 кг, третья − 1,66 кг, а четвёртая − 15,875 кг. Найдите общую массу этих четырёх деталей и округлите результат до десятых долей килограмма. Сравните ответ с результатом, полученным, если сначала округлить данные задачи до десятых долей, а потом её решить.

Решение

Общая масса деталей равна 13,26 + 14,43 + 1,66 + 15,875 = 45,225 (кг)
45,225 кг ≈ 45,2 кг
13,26 кг ≈ 13,3 кг;
14,43 кг ≈ 14,4 кг;
1,66 кг ≈ 1,7 кг;
15,875 кг ≈ 15,9;
13,3 + 14,4 + 1,7 + 15,9 = 45,3 (кг)
видно, что результат округления суммы не равен сумме округлённых слагаемых.

Задание 426

Трасса лыжных гонок состоит из 4 участков. Первый участок имеет длину 4,35 км, второй − 5,75 км, третий − 6,95 км и четвёртый − 2,8 км. Найдите длину всей трассы и округлите ответ:
а) до десятых долей километра;
б) до целых километров.

Решение

а)  4,35 + 5,75 + 6,95 + 2,8 = 19,85 (км) - длина всей трассы
     19,85 км ≈ 19,9 км
Ответ: 19,9 км.

б)  4,35 + 5,75 + 6,95 + 2,8 = 19,85 (км) - длина всей трассы
    19,85 км ≈  20 км
Ответ: 20 км.

Задание 427

Найдите периметр четырёхугольника ABCD, если АВ = 6,2 дм, CD больше АВ на 3,14 дм, но меньше ВС на 2,31 дм; AD больше ВС на 1,2 дм. Ответ округлите:
а) до десятых долей дециметра;
б) до целых дециметров.

Решение

а) CD = 6,2 + 3,14 = 9,34 (дм)
ВС = 9,34 + 2,31 = 11,65 (дм)
AD = 11,65 + 1,2 = 12,85 (дм)
PABCD = 6,2 + 9,34 + 11,65 + 12,85 = 40,04 (дм)
40,04 дм ≈ 40,0 дм.

б) CD = 6,2 + 3,14 = 9,34 (дм)
ВС = 9,34 + 2,31 = 11,65 (дм)
AD = 11,65 + 1,2 = 12,85 (дм)
PABCD = 6,2 + 9,34 + 11,65 + 12,85 = 40,04 (дм)
40,04 дм ≈ 40 дм.

Задание 428

Вычислите устно:
а)6² + 2²
+ 50
: 15
* 20
− 25
?
б) 3³ + 5²
: 13
* 25
+ 150
: 125
?
в) 4³ − 3²
: 11
* 40
− 75
: 25
?
г) 2³ + 9²
+ 21
: 11
* 18
: 45
?

Решение

а) 36 + 4 = 40, 90, 6, 120, 95.

б) 27 + 25 = 52, 4, 100, 250, 2.

в) 64 − 9 = 55, 5, 200, 125.

г) 8 + 81 = 89, 110, 10, 180, 4.

Задание 429

Восстановите цепочку вычислений: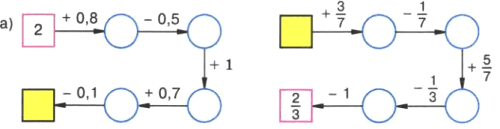

Решение

а) 2 → 2,8 → 2,3 → 3,3 → 4 → 3,9

б) 1 → 1 3/7 → 1 2/7 → 2 → 1 2/3 → 2/3

Задание 430

На координатном луче число х расположено между числами а и b. Определите, к какому из чисел ближе х, если:
а) а = 2,3, b = 2,7, х = 2,6;
б) а = 1,34, b = 1,35, х = 1,342;
в) а = 5,6, b = 5,7, х = 5,65.

Решение

а) x расположено ближе к числу b:
х − а = 2,6 − 2,3 = 0,3 > b − х − 2,7 − 2,6 = 0,1

б) х расположено ближе к числу а:
х − а = 1,342 − 1,34 = 0,002 < b − х = 1,35 − 1,342 = 0,008

в) х расположено на одинаковом расстоянии от чисел а и b:
х − а = 5,65 − 5,6 = 0,05 = b − х = 5,7 − 5,65 = 0,05

Задание 431

К числу 76890 приписали справа нуль, два нуля, три нуля. Во сколько раз увеличилось число? Прочитайте каждое из получившихся чисел.

Решение

Число увеличилось в 10 раз;
768900 − семьсот шестьдесят восемь тысяч девятьсот. Число увеличилось в 100 раз;
7689000 − семь миллионов шестьсот восемьдесят девять тысяч. Число увеличилось в 1000 раз;
76890000 − семьдесят шесть миллионов восемьсот девяносто тысяч.

Задание 432

В числе 89452200 зачеркнули два последних нуля. Во сколько раз уменьшилось число?

Решение

Число уменьшилось в 100 раз.

Задание 433

Укажите два числа, которые на координатном луче расположены между числами:
а) 2,1 и 2,2;
б) 0,8 и 0,9;
в) 0 и 0,02;
г) 3,1 и 3,11.

Решение

а) 2,1 < 2,15 < 2,17 < 2,2

б) 0,8 < 0,85 < 0,89 < 0,9

в) 0 < 0,015 < 0,018 < 0,02

г) 3,1 < 3,101 < 3,102 < 3,11

Задание 434

Шахматная доска состоит из 8 рядов по 8 клеток в каждом из них. Какую часть доски составляет:
а) один ряд клеток;
в) одна клетка;
б) 3 ряда клеток;
г) 7 клеток?
Шахматный конь может двигаться на две клетки по вертикали или горизонтали и на одну клетку в сторону. Подумайте, может ли конь переместиться из клетки А шахматной доски в клетку В.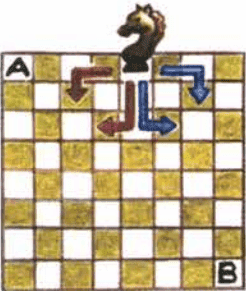

Решение

а) Всего на шахматной доске 8 * 8 = 64 клетки:
1 ряд клеток = 8 клеткам = 8/64 = 1/8 шахматной доски.

б) Всего на шахматной доске 8 * 8 = 64 клетки:
3 ряда клеток = 24 клеткам = 24/64 = 3/8 шахматной доски.

в) Всего на шахматной доске 8 * 8 = 64 клетки:
1 клетка = 1/64 доски.

г) Всего на шахматной доске 8 * 8 = 64 клетки:
7 клеток = 7/64 шахматной доски.

Да, шахматный конь может переместиться из клетки А в клетку В.

Задание 435

Какую часть кубического метра составляет:
а) 1 л;
б) 10 дм³;
в) 100 л;
г) 100 см³?

Решение

а) 1л = 1/1000 = 0,01 м³

б) 10 д м 3 = 10/1000 = 0,01 м³

в) 100 л = 100/1000 = 0,01 м³

г) 100 см³ = 100/1000000 = 0,0001 м³

Задание 436

Найдите число, которое:
а) на 1 3/11 больше 3 7/11;
б) на 8/17 меньше 1.

Решение

а) $3\frac7{11}+1\frac3{11}=3+1+\frac7{11}+\frac3{11}=4\frac{10}{11}$

б) $1-\frac8{17}=\frac{17}{17}-\frac8{17}=\frac9{17}$

Задание 437

Используя рисунок 150, найдите число а: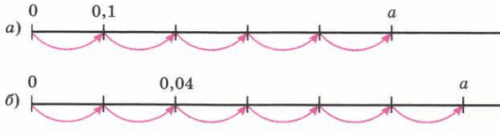

Решение

а) a = 0,1 + 0,1 + 0,1 + 0,1 + 0,1 = 0,5

б) a = 0,04 + 0,04 + 0,04 = 0,12

Задание 438

Согласны ли вы с утверждением: «Если участки огорожены заборами одинаковой длины, то площади этих участков равны»? Подтвердите своё мнение примерами.

Решение

Это утверждение неверно. Например, прямоугольный участок длиной 6 м и шириной 12 м имеет
Р = 2 * (6 + 12) = 36 м;
S = 6 * 12 = 72 м², но квадратный участок со стороной 9 м имеет такой же
Р = 4 * 9 = 36 м, но S = 9 * 9 = 81 м².

Задание 439

Скорость течения реки 60 м/мин. Продвигается ли лодка, в каком направлении и с какой скоростью, если её собственная скорость:
а) 90 м/мин направлена по течению;
б) 90 м/мин направлена против течения;
в) 60 м/мин направлена по течению;
г) 60 м/мин направлена против течения?

Решение

а) 60 + 90 = 150 (м/мин) - скорость лодки по течению реки
Ответ: лодка движется по течению со скоростью 150 м/мин.

б) 90 − 60 = 30 (м/мин) - скорость лодки против течения реки
Ответ: лодка движется против течения со скоростью 30 м/мин

в) 60 + 60 = 120 (м/мин) - скорость лодки по течению реки
Ответ: лодка движется по течению со скоростью 120 м/мин

г) 60 − 60 = 0 (м/мин) - скорость лодки против течения, то есть лодка не двигается.
Ответ: лодка не движется.

Задание 440

Запишите 4 числа, первое из которых 4,612, а каждое следующее на 2,154 больше предыдущего.

Решение

4,612 + 2,154 = 6,766
6,766 + 2,154 = 8,92
8,92 + 2,154 = 11,074
Ответ: 4,612; 6,766; 8,92; 11,074

Задание 441

Найдите значение выражения 84 − а и выражения а + 6,546,
если a = 30,4; 2,454; 83,998.

Решение

при a = 30,4
84 − a = 84 − 30,4 = 53,6;
a + 6,546 = 30,4 + 6,546 = 36,946;

при a = 2,454
84 − a = 84 − 2,454 = 81,546;
a + 6,546 = 2,454 + 6,546 = 9;

при a = 83,998
84 − a = 84 − 83,998 = 0,002;
a + 6,546 = 83,998 + 6,546 = 90,544.

Задание 442

Представьте произведение 2,75 * 3 в виде суммы и найдите его значение.

Решение

2,75 * 3 = 2,75 + 2,75 + 2,75 = 5,5 + 2,75 = 8,25.

Задание 443

Выполните действия:
а) 68,7 − (44 + 0,375);
б) 90,4 + 65,4 − 90,8;
в) 504 − 47,9 + (58,7 − 49);
г) 17,654 − (37 − 22,9) + 0,345.

Решение

а) 68,7 − (44 + 0,375) = 68,7 − 44,375 = 24,325

б) 90,4 + 65,4 − 90,8 = 155,8 − 90,8 = 65

в) 504 − 47,9 + (58,7 − 49) = 456,1 − 9,7 = 465,8

г) 17,654 − (37 − 22,9) + 0,345 = 17,654 − 14,1 + 0,345 = 3,554 + 0,345 = 3,899

Задание 444

Вместо звёздочки поставьте знак >, = или < так, чтобы получилось верное равенство или неравенство:
а) 0,483 * 0,479;
б) 4,781 * 4,79;
в) 95,3 * 95,300;
г) 0,045 * 0,0045.

Решение

а) 0,483 > 0,479

б) 4,781 < 4,79

в) 95,3 = 95,300

г) 0,045 > 0,0045

Задание 445

Собственная скорость лодки 4,5 км/ч, скорость течения 2,5 км/ч. Найдите скорость лодки при движении по течению и против течения. Какой путь пройдёт лодка по течению за 4 ч и какой путь она пройдёт против течения за 3 ч?

Решение

1) 4,5 + 2,5 = 7 (км/ч) - скорость лодки по течению
2) 4,5 − 2,5 = 2 (км/ч) - скорость лодки против течения
3) 7 * 4 = 28 (км) - пройдет лодка за 4 часа по течению
4) 2 * 3 = 6 (км) - пройдет лодка за 3 ч против течения
Ответ: 28 км, 6 км.

Задание 446

Решите задачу:
1) В школу завезли 24 т угля. За зиму израсходовали 7/8 привезённого угля. Сколько тонн угля осталось?
2) Маляры израсходовали 5/6 купленной краски для ремонта школы. Сколько краски осталось, если купили её 300 кг?

Решение

1) 1 − 7/8 = 1/8 привезённого угля осталась
   24 : 8 = 3 (т) - осталось
Ответ: 3 т.

2) 1 − 5/6 = 1/6 купленной краски осталось
    300 : 6 = 50 (кг) - осталось
Ответ: 50 кг.

Задание 447

Округлите дроби:
а) 1,69; 1,198; 37,444; 37,5444; 802,3022 до целых;
б) 0,3691; 0,8218; 0,9702; 81,3501 до десятых.

Решение

а) 1,69 ≈ 2
1,198 ≈ 1
37,44 ≈ 37
37,5444 ≈ 38
802,3022 ≈ 802

б) 0,3691 ≈ 0,4
0,8218 ≈ 0,8
0,9702 ≈ 1,0
81,3501 ≈ 81,4

Задание 448

Для каждого из чисел найдите натуральные приближённые значения с недостатком и с избытком:
3,97; 21,609; 10,394; 1,057.

Решение

3 < 3,97 < 4
21 < 21,609 < 22
10 < 10,394 < 11
1 < 1,057 < 2

Задание 449

==

Решение

                    76,3681  36,4545  194,0817  97,5983
до дес-ков     80             40           190          100
до един.         76             36            194         98
до десятых    76,4          36,5        194,1       97,6
до сотых        76,37       36,45       194,08     97,60
до тыс-ных    76,368     36,455     194,082   97,598

Задание 450

Запишите число, которое:
а) меньше миллиона в 10 раз; на 10;
б) больше миллиона в 10 раз; на 10;
в) больше числа 709 в 100 раз; в 1000 раз;
г) меньше числа 623 100 000 в 10 раз; в 1000 раз; в 100 000 раз.

Решение

а) 100000, 999990.

б) 10000000, 1000010.

в) 70900, 709000.

г) 62310000, 623100, 6231.

Задание 451

Найдите значение выражения:
а) 8000 * 60000;
б) 1700 * 800000;
в) 250000 * 600 * 40;
г) 19000 * 20000 * 50.

Решение

а) 8000 * 60000 = 480000000

б) 1700 * 800000 = 1360000000

в) 250000 * 600 * 40 = 10000000 * 600 = 6000000000

г) 19000 * 20000 * 50 = 19000 * 1000000 = 19000000000

Задание 452

Собственная скорость теплохода 21,6 км/ч. Скорость течения 4,9 км/ч. Найдите скорость теплохода по течению и против течения.

Решение

1) 21,6 + 4,9 = 26,5 (км/ч) - скорость теплохода по течению
2) 21,6 − 4,9 = 16,7 (км/ч) - скорость теплохода против течения
Ответ: 26,5 км/ч, 16,7 км/ч.

Задание 453

Теплоход шёл по озеру 3 ч со скоростью 27 км/ч, а потом 4 ч по реке, впадающей в это озеро. Найдите весь путь, который прошёл теплоход за эти 7 ч, если скорость течения реки 3 км/ч.

Решение

1)  27 * 7 = 81 (км) - теплоход прошёл по озеру
2) (27 − 3) * 4 = 96 (км) - теплоход прошёл по реке против течения
3) 81 + 96 = 177 (км)- всего прошел теплоход
Ответ: 177 км.

Задание 454

В сокровищнице Кощея Бессмертного 32 000 ларцов, в каждом ларце 210 одинаковых по массе слитков золота и серебра. Какова масса запасов золота и серебра у Кощея, если масса десятка слитков 900 г?

Решение

(32000 * 210) : 100 * 900 = 672000 * 900 = 604800000 (г) - масса запасов золота и серебра
604800000 г = 604,8 т
Ответ: 604,8 т.

Задание 455

Поставьте вместо звёздочек пропущенные цифры:
а) + 6*3*785
         3*4*82
        *9367**
б) + 37*743*
        4*4*2*5
        *106*93

Решение

а) + 6631785
   304982
       6936767

б) + 3757438
4349255
       8106693