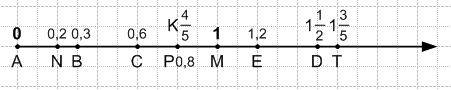Итоговое повторение, стр. 175

Задание 935

Приведите примеры:
а) натуральных чисел;
б) обыкновенных дробей;
в) чисел, не являющихся натуральными;
г) десятичных дробей.

Решение

а) 1; 2; 100; 10000.

б) 1/2 ; 1/3 ; 5/20 ; 10/100.

в) 0 ; 1/3 ; 1,5 ; 0,001.

г) 5,2; 18,5; 100,01; 0,0001.

Задание 936

Среди следующих чисел укажите натуральные:
18 ; 1/2 ; 1 ; 0 , 6 ; 0 ; 105 ; 12 , 4.

Решение

18; 1; 105 − натуральные числа.

Задание 937

Пятизначное число оканчивается цифрой 6. В этом числе переставили две последние цифры, но оно не изменилось. Какая цифра стояла в числе перед цифрой 6?

Решение

6.

Задание 938

На сколько изменится семизначное число, оканчивающееся на 40, если эти две цифры поменять местами?

Решение

***40 − ***04 = 36.

Задание 939

Верно ли, что если цифры, из которых составлено шестизначное число, записать в обратном порядке, то получится опять шестизначное число?

Решение

Нет, если шестизначное число оканчивается на 0.

Задание 940

В каком порядке выполняются действия в выражении без скобок, если в нём встречаются только сложение и деление?

Решение

Сначала деления − слева направо, а затем сложения − слева направо.

Задание 941

Вычислите устно:
а) 10 : 4
- 1,3
* 0,4
+ 0,32
?
б) 4 - 3,4
* 1,4
+ 0,06
: 1,8
?
в) 3 : 300
+ 0,37
: 1,9
* 8
?
г) 70 : 20
: 10
* 4
+ 1,04
?
д) 9,8 : 7
* 3
- 0,3
+ 2,1
?
е) 49 : 70
+ 9,8
: 5
: 0,3
?
ж) 3,9 + 2,7
: 11
* 13
?
з) 4,6 + 2,2
- 30,5
* 0,1
?

Решение

а) 2,5, 1,2, 0,48, 0,8.

б) 0,6, 0,84, 0,9, 0,5.

в) 0,01, 0,38, 0,2, 1,6.

г) 3,5, 0,35, 1,4, 2,44.

д) 1,4, 4,2, 3,9, 6.

e) 0,7, 10,5, 2,1, 7.

ж) 6,6, 0,6, 7,8, 5,05.

з) 6,8, 34, 3,5, 0,35.

Задание 942

Выполните действия:
1) 5555 + (82320 : 84 − 693) * 66;
2) 32087 − 87 * (67 + 62524 : 308);
3) 467915 + 137865 : (31353 − 48 * 609);
4) 51003 − (4968 + 709 * 52) + 203;
5) 612228 + (53007 − 52275 : 615);
6) 343 * (324378 : 54 − 4862) + 777;
7) 18408 : (268 * 75 − 19746) + 959;
8) (86 * 217 + 275116) : 859 + 279569.

Решение

1) 5555 + (82 320 : 84 − 693) * 66 = 5555 + (980 − 693) * 66 = 5555 + 287 * 66 = 555 + 18 942 = 24497

2) 32087 − 87 * (67 + 62524 : 308) = 32087 − 87 * (67 + 203) = 32087 − 87 * 270 = 32087 − 23490 = 8597

3) 467915 + 137865 : (31353 − 48 * 609) = 467915 + 137865 : (31353 − 29232) = 467915 + 137865 : 2121 = 467915 + 65 = 467980

4) 51003 − (4968 + 709 − 52) + 203 = 51003 − (4968 + 36 868) + 203 = 51003 − 41836 + 203 = 9167 + 203 = 9370

5) 612228 + (53007 − 52275 : 615) = 612228 + (53007 − 85) − 612228 + 52922 = 665150

6) 343 * (324378 : 54 − 4862) + 777 = 343 * (6007 − 4862) + 777 = 343 * 1145 + 777 = 392735 + 777 = 393512

7) 18408 : (268 * 75 − 19746) + 959 = 18408 : (20100 − 19746) + 959 = 18408 : 354 + 959 = 52 + 959 = 1011

8) (86 * 217 + 275116) : 859 + 279569 = (18662 + 275116) : 859 + 279569 = 293778 : 859 + 279569 = 342 + 279569 = 279911

Задание 943

Сформулируйте и запишите с помощью букв:
а) свойства сложения чисел;
б) свойства вычитания чисел;
в) свойства умножения чисел.
Приведите примеры, когда использование свойств арифметических действий упрощает вычисления.

Решение

а) a + b = b + a; (a + b) + c = a + (b + c)

б) a − (b + c) = a − b − c, a − (b − c) = a − b + c

в) a − b = b − а; (аb)с = а(bс); (а + b)c = ac + bc; (a − b)c = ac − bc

Задание 944

При каком условии:
а) сумма двух чисел равна одному из них;
б) разность равна уменьшаемому, нулю;
в) произведение равно одному из множителей, нулю;
г) частное равно делимому, нулю, единице?
Как найти делимое, если известны делитель, неполное частное и остаток?

Решение

а) если второе число равно 0

б) если вычитаемое равно 0, уменьшаемое равно вычитаемому

в) если второй множитель равен 1;
если хотя бы один из множителей равен 0.

г) Если делитель равен 1.
Если делимое равно 0, а делитель не равен 0.
Если делимое равно делителю, кроме случая, когда они оба равны 0.

Задание 945

Выполните деление с остатком:
а) 27450 на 89;
б) 30394 на 307.

Решение

а) 27450 = 89 * 308 + 38

б) 30394 = 307 * 99 + 1

Задание 946

При делении числа с на 12 получили в частном 7 и в остатке 5. Чему будут равны частное и остаток при делении числа с на 7?

Решение

Так как 5 < 7, то в остатке также будет 5, а неполное частное будет равно 12.

Задание 947

Найдите значение выражения:
а) 85 + 203x + 102x + 91, если х = 76; 201;
б) 79у − (23у − 15у), если у = 15; 309.

Решение

а) 85 + 203x + 102x + 9 = 305x + 176
При x = 76
305 * 76 + 176 = 23356
При x = 201
305 * 201 + 176 = 61481

б) 79y − (23y − 15y) = 79y − 23y + 15y = 71y
При у = 15
71 * 15 = 1065
При у = 309
71 * 309 = 21939

Задание 948

Какая дробь называется правильной; неправильной? Как представить в виде неправильной дроби число 2 1/7 ; 4?
Как выделить целую часть числа 19/6?

Решение

Правильной называется дробь у которой числитель меньше знаменателя.
Неправильной называется дробь у которой числитель больше или равен знаменателю.
$2\frac17=2+\frac17=\frac{14}7+\frac17=\frac{15}7$
$4=\frac41$
$\frac{19}6=\frac{6\ast3}6+\frac16=3\frac16$

Задание 949

Запишите в виде неправильной дроби число:
а) 3 12/13;
б) 203 11/15;
в) 4 11/12;
г) 704 9/14.

Решение

а) $3\frac{12}{13}=\frac{39}{13}+\frac{12}{13}=\frac{51}{13}$

б) $203\frac{11}{15}=\frac{3045}{15}+\frac{11}{15}$

в) $4\frac{11}{12}=\frac{48}{12}+\frac{11}{12}=\frac{59}{12}$

г) $704\frac9{14}=\frac{9856}{14}+\frac9{14}=\frac{9865}{14}$

Задание 950

Выполните действия:
а) 4 3/8 − ( 3 5/7 − 1 5/7 ) + 1 5/8;
б) 12 7/12 − 4 5/12 − ( 20 3/4 − 19 3/4 ).

Решение

а) $4\frac38-(3\frac57-1\frac57)+1\frac58=4\frac38-2+1\frac58=6-2=4$

б) $12\frac7{12}-4\frac5{12}-(20\frac34-19\frac34)=8\frac2{12}-1=7\frac2{12}$

Задание 951

В коробку положили 15 конфет «Маска», 20 конфет «Ромашка» и 40 ирисок. Какую часть всех конфет составляют конфеты каждого сорта?

Решение

15 + 20 + 40 = 75 (к.) - было всего
масок 15/75,
ромашек 20/75,
а ирисок 40/75.

Задание 952

Сколькими способами 4 пассажира могут разместиться в четырёхместном купе поезда?

Решение

4! = 1 * 2 * 3 * 4 = 24 (с.)
Ответ: 24 способами.

Задание 953

Мастерская за месяц должна сшить 38 костюмов. В первую неделю было сшито 7 костюмов, во вторую − 11 костюмов. Какую часть всех костюмов осталось сшить?

Решение

За первую неделю сшили 7/38,
за вторую неделю 11/38,
за первые две недели сшили 7/38 + 11/38 = 18/38,
тогда осталось сшить 1 − 18/38 = 38/38 − 18/38 = 20/38.

Задание 954

За месяц завод должен отгрузить 42 вагона продукции. В первую неделю отгрузили 12 вагонов, во вторую неделю − 8 вагонов. Какую часть всех вагонов осталось отгрузить заводу?

Решение

В первую неделю отгрузили 12/42, во вторую 8/42,
1 − 12/42 = 42/42 − 12/42 − 8/42 = 22/42 -  часть всех вагонов осталось отгрузить
Ответ: 22/42 часть всех вагонов.

Задание 955

Длина одной стороны четырёхугольника составляет 3/11 его периметра, длина другой 4/11 периметра, а сумма длин этих сторон равна 28 см. Найдите периметр четырёхугольника.

Решение

1) 3/11 + 4/11 = 7/11 - составляет длина первой и второй сторон вместе
2) 28 : 7 * 11 = 44 (см) - периметр
Ответ: 44 см.

Задание 956

Число лет сына составляет 2/11 числа лет отца, а число лет дочери 5/11 числа лет отца. Сколько лет отцу, если сыну и дочери вместе 28 лет?

Решение

1) 2/11 + 5/11 = 7/11 числа лет отца сыну и дочери вместе,
2) 28 : 7 * 11 = 44 (года) - отцу.
Ответ: 44 года.

Задание 957

В палатку привезли 1260 кг картофеля. В первый день было продано 2 3 всего картофеля, во второй день 5/7 г остатка. Сколько килограммов картофеля осталось после двух дней продажи?

Решение

1) 1 − 2/3 = 1/3 всего картофеля осталось после первого дня
2)  1260 * 1/ 3 = 1260 : 3 = 420 (кг) - картофеля осталось после первого дня
3)  1 − 5/7 = 2/7 - картофеля осталось после второго дня
4) 420 * 2/7 = 420 : 7 * 2 = 120 (кг) - картофеля осталось после двух дней продажи
Ответ: 120 кг.

Задание 958

Приняв за единичный отрезок длину 10 клеток тетради, отметьте на луче точки, координаты которых равны:
а) 0 ; 1 ; 0,3 ; 3/5 ; 0,6 ; 1 2/5 ; 1,2;
б) 0 ; 1 ; 0,2 ; 4/5 ; 0,8 ; 1 3/5 ; 1,4.

Решение

Задание 959

Назовите какое−нибудь значение координаты точки С, лежащей на координатном луче между точками А и В, если:
а) А(2) и В(5);
б) А(2) и В(3);
в) А(2,8) и В(3,5);
г) А(2,9) и В(3);
д) А(4/5) и В(1).

Решение

а) C(3,2)

б) С(2,8)

в) С(3)

г) C(2,99)

д) C(0,85)

Задание 960

Как на координатном луче расположены точки А(х) и В(у), если:
а) х > у;
б) х = у;
в) х < у?

Решение

а) А правее В

б) А и В одна и та же точка

в) А левее В

Задание 961

Как сравнить:
а) четырёхзначное и пятизначное натуральные числа;
б) два шестизначных числа, первое из которых начинается цифрой 7, а второе − цифрой 5;
в) натуральное число и 0;
г) обыкновенные дроби с одинаковыми знаменателями;
д) десятичные дроби с разными целыми частями;
е) десятичные дроби с одинаковыми целыми частями?

Решение

а) Пятизначное всегда больше четырехзначного

б) То число, которое начинается на 7 всегда больше того, что начинается на 5

в) Натуральное число всегда больше, чем 0.

г) Из двух обыкновенных дробей с одинаковыми знаменателями больше то, у которого больше числитель

д) Из двух десятичных дробей с разными целыми частями больше то, у которой больше целая часть.

е) Из двух десятичных дробей с одинаковыми целыми частями больше та, у которой больше дробная часть.

Задание 962

Сравните числа:
а) 4357 и 986;
б) 7615 и 7613;
в) 0,75 и 1,000;
г) 12,815 и 2,819;
д) 1,2 и 1 3/5;
е) 3/4 и 7/8;
ж) 1 3/5 и 1 1/2;
з) 1 4/5 и 9/10;
и) 5/8 и 1/2.

Решение

а) 4357 > 986

б) 7615 > 7613

в) 0,75 < 1,000

г) 12,815 > 2,819

д) 1,2 < 1 3/5

е) 3/4 = 6/8 < 7/8

ж) 1 3/5 = 1,6 > 1 1/2 = 1,5

з) 1 4/5 = 1,8 < 9/10 = 1,9

и) 5/8 > 1/2 = 4/8

Задание 963

Приведите примеры округления:
а) натурального числа до тысячи;
б) десятичной дроби до единиц;
в) десятичной дроби до сотых.

Решение

а) 1900 ≈ 2000; 23100 ≈ 23000.

б) 0,6 ≈ 1; 0,01 ≈ 0.

в) 0,052 ≈ 0,05; 10,602 ≈ 10,60.

Задание 964

Как найти среднее арифметическое нескольких чисел? Как найти среднюю скорость?

Решение

Для нахождения среднего арифметического нескольких чисел нужно сумму этих чисел разделить на количество этих чисел. Средняя скорость равна частному от деления пройденного пути на время.

Задание 965

Вычислите устно:
а) 6 : 1,2
- 5
* 0,97
+ 3,15
?
б) 9 : 1,5
- 5
* 0,25
+ 6
?
в) 3 * 1,6
-1,2
: 12
+ 1,2
?
г) 0,6 * 6
+ 1,2
: 40
* 50
?
д) 30 * 3
- 4,8
: 0,7
* 0,01
?
е) 2 * 1,9
- 2,2
: 0,8
: 0,1
?
ж) 7 - 0,7
: 0,9
* 0,02
+ 0,66
?
з) 1,5 * 6
: 5
* 2
+ 2,4
?

Решение

а) 5, 0, 0, 3,15.

б) 6, 1, 0,25, 6,25.

в) 4,8, 3,6, З, 4,2.

г) 3,6, 4,8, 0,12, 6.

д) 9, 4,2, 6, 0,06.

е)3,8, 1,6, 2, 20.

ж) 6,3, 7, 0,14, 0,8.

з) 9, 1,8, 3,6, 6.

Задание 966

На рисунке 188 изображена шкала расстояний от города А до города B. Каждое деление шкалы соответствует расстоянию 20 км. Точками M, N, P отмечены расстояния, которые прошла автомашина через каждый час, двигаясь из города А в город В.
Определите:
а) чему равно расстояние от города А до города В;
б) какое расстояние прошла автомашина за первые два часа; за вторые два часа;
в) на каком расстоянии от города В была автомашина через 2 ч после выхода из города А;
г) какое расстояние прошла автомашина за 3 ч;
д) с какой средней скоростью шла автомашина в первые 2 ч; во вторые 2 ч.

Решение

а) 360 км

б) 180 км; 180 км.

в) 180 км

г) 300 км

д) 180 : 2 = 90 км/ч; 180 : 2 = 90 км/ч.

Задание 967

Какую дробь называют десятичной? Приведите примеры таких дробей и назовите по порядку первые четыре разряда, стоящие в десятичной дроби справа от запятой. Изменится ли десятичная дробь, если к ней справа приписать один или несколько нулей? Как представить обыкновенную дробь в виде десятичной? Приведите пример.

Решение

Десятичная дробью называют дробь, знаменатель которой кратен 10, например: 0,5; 1,1; 100,255;
При приписывании нулей справа от запятой в конец дроби, дробь не меняется:
1/10 = 0,1 ;
5 5/1000 = 5,005.

Задание 968

По какому правилу выполняется:
а) сложение (вычитание) обыкновенных дробей с одинаковыми знаменателями;
б) сложение (вычитание) десятичных дробей;
в) умножение десятичных дробей;
г) умножение десятичной дроби на 10, 100, 1000 и т. д.;
д) деление десятичной дроби на натуральное число;
е) деление числа на десятичную дробь;
ж) умножение десятичной дроби на 0,1; 0,01; 0,001 и т. д.;
з) деление десятичной дроби на 10, 100, 1000 и т. д.;
и) деление десятичной дроби на 0,1; 0,01; 0,001 и т. д.?

Решение

а) Числители складываются (вычитаются), а знаменатель остается тем же.

б) Как натуральные числа, с учётом запятой.

в) Дроби умножаются как натуральные числа, с учётом запятой.

г) Запятая сдвигается вправо на 1; 2; 3 знака и т. д.

д) Дробь делится на число, только в частном запятая сдвигается влево на число знаков после запятой в делимом.

е) Число делится на дробь, только в частном запятая сдвигается вправо на число знаков после запятой в делителе.

ж) В дроби запятая сдвигается влево на 1; 2; 3 знака и т. д.

з) В дроби запятая сдвигается влево на 1; 2; 3 знака и т. д.

и) В дроби запятая сдвигается вправо на 1; 2; 3 знака и т. д.

Задание 969

Найдите значение выражения:
а) 427 051 : 839 − 390 912 : 768 + 252 000 : 1260 + 249 249 : 249;
б) 917 580 : (194 + 25 * 37) − 386;
в) (23,79 : 7,8 − 6,8 : 17) * 3,04 − 2,04 * 0,85;
г) (15,36 − 4,36 * (20,74 : 6,8 − 7,6 : 19)) * 0,25;
д) ((3,2 + 0,32) : 0,1 − (50 − 7,2) * 0,1) * 100;
е) ((4,3 − 1,08) : 0,1 + (40 − 8,4) * 0,1) * 100.

Решение

а) 427051 : 839 − 390912 : 768 + 252000 : 1260 + 249249 : 249 = 509 − 509 + 200 + 1001 = 1201

б) 917580 : (194 + 25 * 37) − 386 = 917580 : (194 + + 925) − 386 = 917580 : 1119 − 386 = 820 − 386 = 434

в) (23,79 : 7,8 − 6,8 : 17) * 3,04 − 2,04 * 0,85 = (3,05 − 0,4) * 3,04 − 1,734 = 2,65 * 3,04 − 1,734 = 8,056 − 1,734 = 6,322

г) (15,36 − 4,36 * (20,74 : 6,8 − 7,6 : 191)) * 0,25 = (15,36 − 4,36 * (3,05 − 0,4) * 0,25 = (15,36 − 4,36 * 2,65) * 0,25 = (15,36 − 11,55) * 0,25 = 3,806 * 0,25 = 0,9515

д) ((3,2 + 0,32) : 0,1 − (50 − 7,2) * 0,1) * 100 = (3,52 : 0,1 − 42,8 * 0,1) * 100 = (35,2 − 4,28) * 100 = 30,92 * 100 = 3092

e) ((4,3 − 1,08) : 0,1 + (40 − 8,4) * 0,1) * 100 = (3,22 : 0,1 + 31,6 * 0,1) * 100 = (32,2 + 3,16) * 100 = 35,36 * 100 = 3536

Задание 970

Найдите значение выражения:
а) 8 * (1,4x + 13,6y) + 13 * (0,8x − 0,6у) при х = 1; у = 1;
б) 3 * (2,9р − 1,9m) + 2 * (2,3р + 0,7m) при р = 0,1; m = 0.

Решение

а) 8 * (1,4x + 13,6y) + 13 * (0,8x − 0,6y) = 8 * 1,4x + 8 * 13,6у + 13 * 0,8х − 13 * 0,6y =
= 11,2x + 10,4x + 108,8y − 7,8y = 21,6x + 101y;
при x = 1, у = 1 => 21,6 * 1 + 101 * 1 = 21,6 + 101 = 122,6.

б) 3 * (2,9р − 1,9m) + 2 * (2,3р + 0,7m) = 3 * 2,9р − 3 * 1,9m + 2 * 2,3р + 2 * 0,7m = 8,7р − 5,7m + 4,6р + 1,4m = 13,3р − 4,3m;
при р = 0,1, m = 0 => 13,3 * 0,1 − 4,3 * 0 = 1,33.

Задание 971

Надо было перевезти 51 т зерна. Зерно перевозили в машине с двумя прицепами. Сколько сделали поездок, если в кузов машины входило 4,8 т зерна, а в каждый из прицепов − 2,7 т?

Решение

1) 4,8 + 2,7 * 2 = 4,8 + 5,4 = 10,2 (т) - может перевезти машина с двумя прицепами за один раз
2) 51 : 10,2 = 5 (поездок) - потребуется для перевозки 51 т зерна
Ответ: 5 поездок.

Задание 972

За первые 14 рабочих дней завод изготовил 560 стиральных машин, а затем стал изготавливать в день на 5 машин больше. Сколько машин выпустил завод за 20 рабочих дней?

Решение

1) 560 : 14 = 40 (м.)  - в день изготавливал завод сначала
2) 20 − 14 = 6 (д.) - завод работал с повышенной производительностью
3) 40 + 5 = 45 (м.) - стал изготавливать завод в день
4) 45 * 6 = 270 (м.) - изготовил завод за последние 6 дней
4) 560 + 270 = 830 (м.) - изготовил завод за 20 дней
Ответ: 830 машин.

Задание 973

Отцу 40 лет, сыну 5 лет. Во сколько раз отец будет старше сына через 2 года? На сколько лет отец старше сына сейчас и на сколько лет будет старше через 2 года?

Решение

1) 40 − 5 = на 35 (лет) - отец старше сына сейчас
2)  40 + 2 = 42 (г.) будет отцу через 2 года,
3) 5 + 2 = 7 (лет) - будет сыну
4) 42 : 7 = в 6 (раз) - отец будет старше сына
Ответ: в 6 раз.

Задание 974

В классе 7 человек хорошо умеют плавать. Сколькими способами из них можно составить команду из трёх человек для участия в школьных соревнованиях?

Решение

7 * 6 * 5 = 210 (с.) - можно составить команду
Ответ: 210 способами.

Задание 975

По какому правилу находится
а) неизвестное слагаемое;
б) неизвестное уменьшаемое;
в) неизвестное вычитаемое;
г) неизвестный множитель;
д) неизвестное делимое;
е) неизвестный делитель?

Решение

а) из суммы вычитается известные слагаемые

б) к разности прибавляется вычитаемое

в) из уменьшаемого вычитается разность

г) произведение делится на известный множитель

д) делитель умножается на частное

е) делимое делится на частное

Задание 976

Решите уравнение:
а) 22x + х − 10 = 59;
б) 14у − 2у + 76 = 100;
в) (7а − 2а) * 8 = 80;
г) (15b + b) : 4 = 3;
д) (0,87m − 0,66m) * 10 : 2 : 3 = 0;
е) 10 * (1,37k − 0,12k) : 5 : 8 = 0.

Решение

а) 22z + x − 10 = 59
23x = 59 + 10
x = 69 : 23
х = 3

б) 14y − 2y + 76 = 100
12y = 100 − 76
у = 24 : 12
у = 2

в) (7a − 2a) * 8 = 80
5a = 80 : 8 
a = 10 : 5
а = 2

г) (15b + b) : 4 = 3
16b = 3 * 4 
16b =  12
b = 12 : 16
b = 0,75

д) (0,87m − 0,66m) * 10 : 2 : 3 = 0
0,87m − 0,66m = 0
(0,87 − 0,66) * m = 0
m = 0

е)10 * (1,37k − 0,12k) : 5 : 8 = 0
1,37k − 0,12k = 0
(1,37 − 0,12) * k = 0
k = 0

Задание 977

В одном пакете 3 яблока и 10 слив, а в другом − 3 яблока и 15 слив. Какова масса одного яблока и какова масса одной сливы, если масса первого пакета 0,5 кг, а масса второго 0,6 кг?

Решение

1) 15 - 10 = 5 (с.) - на столько больше слив во втором пакете
2) 0,6 − 0,5 = 0,1 (кг) - масса пяти слив
3) 0,1 : 5 = 0,02 (кг) - масса одной сливы
4) 0,5 − 0,02 * 10 = 0,3 (кг) - весят 3 яблока
5) 0,3 : 3 = 0,1 (кг) - весит одно яблоко
Ответ: 0,1 кг и  0,02 кг.

Задание 978

Масса деревянного бруска объёмом 4 дм³ равна 2,8 кг. На сколько килограммов масса стального бруска такого же объёма больше, если известно, что масса стального бруска объёмом 3 дм³ равна 23,4 кг?

Решение

1) 23,4 : 3 = 7,8 (кг) - масса 1 дм³ стали
2) 7,8 * 4 = 31,2 (кг) - весят 4 дм³ стали
3) 31,2 − 2,8 = 28,4 (кг) - на столько 4 дм³ стали тяжелее 4 д м 3 дерева
Ответ: на 28,4 кг.

Задание 979

Масса слонихи вместе со слонёнком равна 7,2 т. Какую массу имеет слонёнок, если он легче слонихи в 5 раз?

Решение

Пусть масса слоненка х,
тогда масса слонихи 5х.
Составим уравнение:
х + 5х = 7,2
6х = 7,2
х = 7,2 : 6
х = 1,2
Значит, 1,2 т весит слоненок
Ответ: 1,2 т.

Задание 980

Саша спросил Сеню: «Сколько тебе лет?» Сеня ответил: «Если число моих лет увеличить в 3 раза, а потом уменьшить на 17, то получится 16 лет». Сколько лет Сене?

Решение

Пусть Сене х лет
Составим уравнение:
3х − 17 = 16
3х = 33
х = 11
Значит, Сене 11 лет.
Ответ: 11 лет.

Задание 981

Если число лет Кати увеличить на 11 и полученный результат уменьшить в 6 раз, то будет 4. Сколько лет Кате?

Решение

Пусть Кате х лет
Составим уравнение:
(х + 11) : 6 = 4
х + 11 = 4 * 6
х = 24 − 11
х = 13
Значит, Кате 13 лет.
Ответ: 13 лет.

Задание 982

Один раз в год наступают сутки, когда день на 40 мин длиннее ночи. Сколько времени длится ночь в эти сутки?

Решение

Пусть ночь длится х мин,
тогда день длится х + 40 мин,
60 * 24 = 1440 (мин) - всего в сутках.
Составим уравнение:
х + (х + 40) = 1440
2х = 1440 − 40
х = 1400 : 2
х = 700
Значит, 700 минут длится ночь
700 мин = 11 ч 40 мин.
Ответ: 11 ч 40 мин.

Задание 983

На чтение девочка потратила в 3 раза меньше времени, чем на прогулку. Сколько времени заняла прогулка, если она продолжалась на 40 мин больше, чем чтение?

Решение

Пусть прогулка у девочки длилась х минут,
тогда чтение (х : 3) мин.
Составим уравнение:
х − х : 3 = 40
2х = 40 * 3
х = 120 : 2
х = 60
Значит, 60 минут длилась прогулка.
60 мин = 1 час.
Ответ: 1 час.

Задание 984

Что называется процентом? Как найти один процент числа? Как найти несколько процентов числа?

Решение

Процентом называется одна сотая часть. Чтобы найти 1% от числа, нужно число разделить на 100.
Чтобы найти 5 процентов от числа, нужно число разделить на 100 и умножить на 5.

Задание 985

На складе было 3,2 т риса. 80% всего риса отправили в магазин и палатку, причём в магазин отправили на 1,28 т больше, чем в палатку. Сколько риса отправили в палатку?

Решение

Пусть в палатку отправили х т,
тогда в магазин х + 1,28 т,
а всего в палатку и магазин 3,2 : 100 * 80 = 2,56 т.
Составим уравнение:
х + (х + 1,28) = 2,56
2х = 2,56 − 1,28
х = 1,28 : 2
х = 0,64
Значит, 0,64 т отправили в палатку.
Ответ: 0,64 т.

Задание 986

На дровяном складе продали в первый день 17% всех дров, во второй день − 18%, а в третий − лишь 5% всех дров. После этого на складе осталось 6000 м³ дров. Сколько кубических метров дров было на складе и сколько продали в первый день?

Решение

1) 100 − (17 + 18 + 5) = 60% (д.) осталось на складе
2) 6000 : 60 * 100 = 10000 (м³) - дров было на складе
3) 10000 : 100 * 17 = 1700 (м³) - дров продали в первый день
Ответ: 10000 м³ и 1700 м³.

Задание 987

Какие отрезки, лучи и прямые на рисунке 189 пересекаются? Какие из этих фигур пересекают окружность?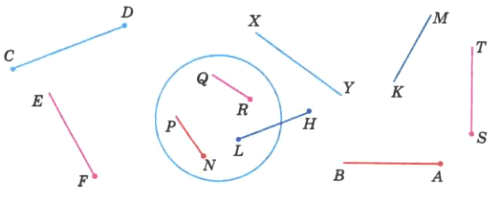

Решение

Пересекаются: FE и NP, FE и RQ, XY и KM, XY и LH, XY и AB, ST и KM, AB и KM, KM и NР, NP и RQ.
Окружность пересекают: NP, RQ, LH, AB, KM.

Задание 988

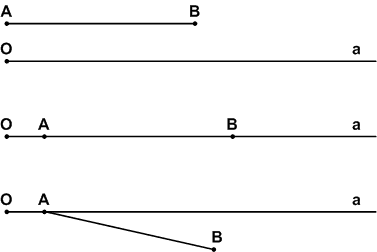
Выполните рисунки:
а) начертите отрезок и отметьте точку, лежащую на отрезке, и точку, не лежащую на нём;
б) начертите прямую и отметьте на ней точку М; ответьте, как называются части, на которые точка М делит прямую;
в) начертите отрезок и луч так, чтобы они не пересекались; чтобы отрезок лежал на луче; чтобы отрезок и луч имели одну общую точку;
г) начертите угол и прямую так, чтобы прямая пересекала только одну сторону угла.

Решение

а)


б) Точка М делит прямую на два луча.


в)

г) 

Задание 989

Можно ли сравнить:
а) два отрезка, зная их длины;
б) два угла, зная их градусные меры?

Решение

а) Из двух отрезков больше тот, у которого больше длина.

б) Из двух углов больше тот, у которого больше градусная мера.

Задание 990

На луче РК взята точка М так, что РМ = 5 см. Сколько отрезков длиной 3 см можно отложить на луче от точки М? Сколько отрезков длиной 7 см можно отложить на луче от точки М?

Решение

Отрезки длиной 3 см можно отложить влево 1, а вправо любое количество;
длиной 7 см − влево ни одного, а вправо любое количество.

Задание 991

На прямой отмечены точки А, В, С и D (рис. 190) так, что АВ = CD. Поставьте вместо звёздочки знак или = так, чтобы для длин отрезков получилось верное равенство или неравенство:
а) ВА * DC;
б) АС * СВ;
в) АС * BD;
г) AD* ВС.

Решение

а) ВА = DC

б) АС > СВ

в) АС = BD

г) AD > ВС

Задание 992

На отрезке MN отмечены две точки С и D так, что точка С лежит между точками N и D. Найдите длину отрезка MNy если DC = 2 см, DN = 6 см, МС = 5 см.

Решение

MN = MD + DC + CN = (MC − DC) + DC + DN − DC = MC + DN − DC = 6 + 5 − 2 = 9 см.

Задание 993

Стороны многоугольника ABCDE равны: АВ = 6,4 см, ВС = 5 см, CD = 6,3 см, DE = 5,8 см и АЕ = 3 см. Найдите периметр этого многоугольника. Как называется такой многоугольник? Что такое периметр многоугольника?

Решение

PABCDE = AB + BC + CD + DE + AE = 6,4 + 5 + 6,3 + 5,8 + 3 = 26,5 см.
ABCDE − пятиугольник.

Задание 994

С помощью какого инструмента можно найти:
а) длину отрезка;
б) градусную меру угла?
В каких единицах измеряются эти величины?

Решение

а) с помощью линейки

б) с помощью транспортира

Длина измеряется в миллиметрах, сантиметрах, дециметрах, метрах и километрах.
Углы измеряется в градусах.

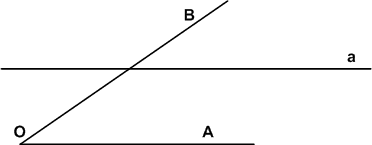
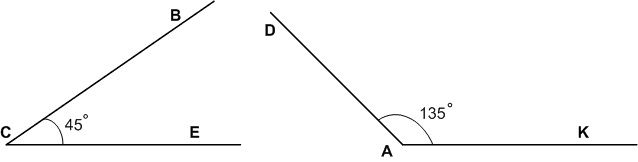
Задание 995

Начертите острый угол ВСЕ и тупой угол DAK и определите их градусные меры. Начертите прямой угол Р и развёрнутый угол М. Какова градусная мера прямого угла? развёрнутого угла? Какую часть развёрнутого угла составляет угол в 1°?

Решение

∠ВСЕ = 45° < 90° − острый угол, 90° < ∠DAK = 135° < 180° − тупой угол,
∠P = 90° − прямой угол, ∠M = 180° − развернутый угол.
Угол в 1° составляет 1/180 часть развернутого угла.

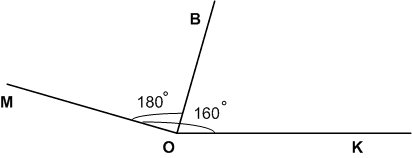
Задание 996

Начертите угол МОК в 160°. Проведите луч ОВ так, чтобы он разделил угол МОК пополам. Как называется такой луч?

Решение

Луч ОB называется биссектрисой угла МОК.

Задание 997

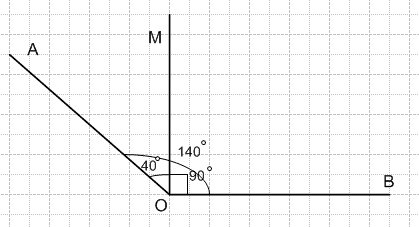
Начертите четырёхугольник ABCD, у которого ∠A = 40°, ∠B = 140°, ∠C = 50°. Измерьте величину угла D.

Решение

Величина угла ∠D = 130°.

Задание 998

Угол АОВ на рисунке 191 разделён на 5 равных углов. Назовите углы, которые составляют 3/5 угла АОВ. Найдите величину угла СОР, если угол АОВ равен 100°.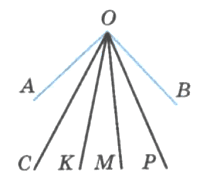

Решение

∠ AOM =∠ COP =∠ KOB = 3/5 ∠ AOB;
∠ COP = 100 * 3/5 = 60 °.

Задание 999

На рисунке 192 угол АОС равен углу DOB. Докажите, что угол АО В равен углу COD.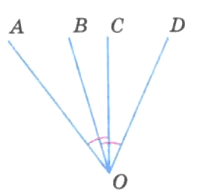

Решение

∠AOB + ∠DOB = ∠AOD;
∠COD + ∠AOC = ∠AOD;
∠AOB = ∠AOD − ∠DOB;
∠COD = ∠AOD − ∠AOC.
Так как ∠DOB = ∠AOC => ∠AOB = ∠COD.

Задание 1000

Прямые АВ и CD (рис. 193) пересекаются в точке О. Докажите, что углы АОС и BOD равны.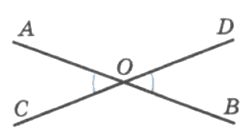

Решение

∠AOB = ∠COD = 180°;
∠COD = ∠AOC + ∠AOD;
∠AOB = ∠AOD + ∠BOD;
∠AOD + ∠AOC = ∠AOD+ ∠BOD;
∠AOC = ∠BOD + ∠AOD − ∠AOD;
∠AOC = ∠BOD.

Задание 1001

Не пользуясь транспортиром, определите угол между стрелками часов на рисунке 194.

Решение

а) 30° * 2 = 60°

б) 5 * 30° = 150°

в) 1,5 * 30° = 45°

г) 3,5 * 3° = 10,5°

д) 4,5 * 30° = 135°

Задание 1002

Вычислите устно:
а) 0,5 * 4
: 0,1
- 0,8
: 30
?
б) 2 - 0,6
* 0,3
: 6
+ 0,23
?
в) 7,2 : 0,1
: 7,2
* 0,36
+ 0,7
?
г) 7,5 * 10
: 50
: 5
* 0,4
?
д) 57 * 0,1
: 3
+ 4,4
: 0,9
?
ж) 0,82 - 0,4
: 0,6
* 5
- 2,5
?
з) 4,4 : 11
: 0,1
* 0,25
: 20
?
е) 0,25 * 2
* 0,6
+ 3,7
: 10
?

Решение

а) 2, 20, 19,2, 0,64.

б) 1,4, 4,2, 0,7, 0,93.

в) 7,2, 10, 3,6, 4,3.

г) 75, 1,5, 0,3, 0,12.

д) 5,7, 1,9, 6,3, 7.

e) 0,42, 0,7, 3,5, 1.

ж) 0,4, 4, 1, 0,05.

з) 0,5, 0,3, 4, 0,4.

Задание 1003

Паша пустился догонять Борю, когда тот отбежал от него на 360 м, и догнал через 9 мин. С какой скоростью бежал Паша, если скорость Бори была 0,2 км/мин?

Решение

Пусть х - скорость Паши,
тогда он догонял Борю со скоростью х − 0,2 , это скорость сближения.
Составим уравнение:
(х − 0,2) * 9 = 0,36
х − 0,2 = 0,04
х = 0,240
Значит, скорость Паши 0,240 км/мин.
Ответ: 0,240 км/мин.

Задание 1004

Серёжа стал догонять Колю, когда тот находился от него на расстоянии 840 м, и догнал через 6 мин. Найдите скорость Коли, если его скорость была в 2 раза меньше скорости Серёжи.

Решение

Пусть х − скорость Коли,
тогда 2х − скорость Сережи.
Составим уравнение:
(2х − х) * 6 = 840
х = 840 : 6
х = 140
Значит, скорость Коли 140 м/мин.
Ответ: 140 м/мин.

Задание 1005

Из двух пунктов одновременно навстречу друг другу вышли грузовая и легковая машины. Скорость грузовой автомашины в 2 раза меньше скорости легковой. Найдите скорость каждой автомашины, если известно, что расстояние между пунктами 480 км и машины встретились через 4 ч.

Решение

Пусть скорость грузовой машины − х,
тогда скорость легковой − 2x.
Составим уравнение:
(х + 2x) * 4 = 480
3х = 480 : 4 = 120
х = 120 : 3
х = 40 
Значит, 40 км/ч − скорость грузовой машины,
40 * 2 = 80 (км/ч) - скорость легковой машины
Ответ: 40 км/ч и 80 км/ч.

Задание 1006

Два поезда вышли навстречу друг другу одновременно из двух городов, расстояние между которыми 592 км. Через 4 ч они встретились. Какова скорость каждого поезда, если известно, что скорость одного из них на 8 км/ч больше скорости другого?

Решение

Пусть х − скорость первого поезда,
тогда х + 5 − скорость второго поезда.
Составим уравнение:
х * 3 + (х + 5) * 3 = 495
3х + 3х = 495 − 15
х = 480 : 6
х = 80
Значит, 80 км/ч − скорость первого поезда,
80 + 5 = 85 (км/ч) − скорость второго поезда.
Ответ: 80 км/ч и 85 км/ч.

Задание 1007

Из города А в город В выехал велосипедист. Через 3 ч после его выезда навстречу ему из города В выехал мотоциклист со скоростью 42 км/ч. Через 2 ч после выезда мотоциклиста они встретились. Найдите скорость велосипедиста, если расстояние между городами А и В равно 144 км.

Решение

Пусть х − скорость велосипедиста,
он ехал 3 + 2 = 5 часов.
Составим уравнение:
5х = 144 − 2 * 42 = 144 − 84 = 60
х = 60 : 5
х = 12
Значит, скорость велосипедиста 12 км/ч.
Ответ: 12 км/ч.

Задание 1008

Из одного и того же пункта одновременно в противоположных направлениях вышли два пешехода. Через 3 ч расстояние между ними стало 21 км. Найдите скорость второго пешехода, если скорость первого 4 км/ч.

Решение

Пусть х − скорость второго пешехода,
тогда скорость удаления пешеходов x + 4 км/ч.
Составим уравнение:
(х + 4) * 3 = 21
х + 4 = 7
х = 7 − 4
х = 3
Значит, скорость второго пешехода 3 км/ч.
Ответ: 3 км/ч.

Задание 1009

Из одной и той же точки шоссе в противоположных направлениях выехали два велосипедиста, один со скоростью 12 км/ч, а другой со скоростью 14 км/ч. Первый велосипедист выехал на час раньше второго. Через сколько времени после выезда первого велосипедиста расстояние между велосипедистами будет равно 64 км?

Решение

Пусть первый велосипедист ехал х часов,
тогда второй ехал х − 1 ч.
Составим уравнение:
12x − 14(х − 1) = 64
12x + 14x − 14 = 64
26х = 64 + 14 = 78
x = 78 : 26
х = 3
Значит, 3 часа ехал первый велосипедист.
Ответ: 3 часа.

Задание 1010

Скорость течения 2,2 км/ч. Собственная скорость катера 15,3 км/ч. Какой путь прошёл катер, если по течению он шёл 3 ч, а против течения 4 ч?

Решение

 (15,3 + 2,2) * 3 + (15,3 − 2,2) * 4 = 104,9 (км) - прошел катер
Ответ: 104,9 км

Задание 1011

Теплоход прошёл по течению 145 км за 5 ч. Сколько времени ему потребовалось на обратный путь, если скорость течения 4,5 км/ч?

Решение

1) 145 : 6 = 29 (км/ч) - скорость теплохода по течению
2)  29 − 2 * 4,5 = 20 (км/ч) - скорость против течения
3)  145 : 20 = 7,25 (ч) -  затратил теплоход на обратный путь
7,25 ч = 7 ч 15 мин. 
Ответ: 7 ч 15 мин.

Задание 1012

Назовите известные вам единицы измерения длины, площади, объёма.

Решение

Длина: метр, сантиметр, миллиметр;
Площадь: га, акр, сотка;
Объем: литр, декалитр, кубический метр.

Задание 1013

Сколько аров в гектаре? квадратных метров в аре? квадратных сантиметров в квадратном дециметре? квадратных сантиметров в квадратном метре?

Решение

1 га = 100 а, 1 а = 100 м², 1 дм² = 100 см², 1 м² = 10000 см².

Задание 1014

Какую часть квадратного сантиметра составляет квадратный миллиметр? Какую часть квадратного метра составляет квадратный сантиметр? Какую часть гектара составляет квадратный метр? Какую часть квадратного километра составляет гектар?

Решение

1 мм² = 0,01 см², 1 см² = 0,0001 м², 1 м² = 0,0001 га, 1 га = 0,01 км².

Задание 1015

Выразите:
а) в метрах: 6 дм, 23 см, 29 дм, 129 см, 2 м 3 дм;
б) в квадратных метрах: 3 дм², 27 дм², 288 дм²;
в) в часах: 11 мин, 35 мин, 73 мин, 1 ч 24 мин;
г) в тоннах: 4 кг, 15 кг, 240 кг, 1250 кг.

Решение

а) 6 дм = 0,6 м
23 см = 0,23 м
29 дм = 2,9 м
129 см = 1,29 м
2 м 3 дм = 2,3 м

б) 3 д м² = 0,03 м²
27 дм² = 0,27 м²
288 дм² = 2,88 м²

в) 11 мин = 11/60 ч
35 мин = 35/60 ч
73 мин = 1 13/60 ч
1 ч 24 мин = 1 24/60 ч

г) 4 кг = 0,004 т
15 кг = 0,015 т
240 кг = 0,24 т
1250 кг = 1,25 т

Задание 1016

Самый длинный день в Москве длится 1057 мин. Выразите в часах продолжительность этого дня. Какова продолжительность самой короткой ночи?

Решение

1057 мин 17 * 30 + 37 мин = 17 ч 37 мин;
24 ч − 17 ч 37 мин = 6 ч 23 мин. - продолжительность самой короткой ночи
Ответ: 6 ч 23 мин.

Задание 1017

Как найти:
а) площадь прямоугольника;
б) площадь квадрата;
в) объём прямоугольного параллелепипеда;
г) объём куба?
Запишите эти правила в виде формул.

Решение

а) S = ab, где а и b − длины его сторон.

б) S = а², где а − длина его стороны.

в) V = аbс, где а, b, с − длины его ребер.

г) V = а³, где а длина ребра куба.

Задание 1018

Сколько кубических сантиметров в кубическом дециметре? Сколько кубических дециметров в кубическом метре? Чему равен литр? Какую долю кубического дециметра составляет кубический сантиметр? Какую долю кубического метра составляет кубический сантиметр?

Решение

1 дм³ = 1000 см³; 1 м³ = 1000 дм³; 1 л = 1 дм³; 1 см³ = 0,001 дм³; 1 с м³ = 0,000001 м³.

Задание 1019

Из скольких прямоугольников состоит поверхность прямоугольного параллелепипеда? Сколько граней, рёбер, вершин имеет прямоугольный параллелепипед? Какой прямоугольный параллелепипед называют кубом? Из каких фигур состоит поверхность куба? Каковы рёбра куба?

Решение

Из 6 прямоугольников; 6 граней, 12 ребер, 8 вершин.
Кубом называется прямоугольный параллелепипед, у которого все ребра равны.
Поверхность куба состоит из 6 квадратов. Все ребра куба равны между собой.

Задание 1020

Как формулируется:
а) свойство площадей равных фигур;
б) свойство площадей фигуры и её частей;
в) свойство объёмов равных фигур;
г) свойство объёмов фигуры и её частей?

Решение

а) площади равных фигур равны

б) площадь фигуры равна сумме площадей ее частей

в) объемы равных фигур равны

г) объем фигуры равен сумме объемов ее частей

Задание 1021

Найдите площадь прямоугольника, стороны которого равны 24,6 см и 18,5 см. Выразите площадь в квадратных дециметрах.

Решение

S = ab = 24,6 * 18,5 = 455,1 см² = 4,551 дм².

Задание 1022

а) Найдите объём прямоугольного параллелепипеда с измерениями 28,2 см, 30 см и 25,5 см и выразите его в кубических дециметрах.
б) Найдите объём куба с ребром 8 дм и выразите его в кубических метрах.

Решение

а) V = abc = 28,2 * 30 * 25,5 = 21573 см³ = 21,573 дм³

б) V = а³ = 83 = 256 дм³ = 0,256 м³

Задание 1023

Два прямоугольника имеют одну и ту же площадь. Длина первого прямоугольника равна 0,6 м, а ширина − 4 дм. Чему равна длина второго прямоугольника, если его ширина 30 см? Найдите и сравните периметры этих прямоугольников.

Решение

0,6 м = 60 см, 4 дм = 40 см;
S = 60 * 40 = 2400 см²,
a = S : b = 2400 : 30 = 80 см.
P 1 = 2 * (60 + 40) = 2 * 100 = 200 см;
P 2 = 2 * (80 + 30) = 2 * 110 = 220 см.
P 2 > P 1.

Задание 1024

Периметр прямоугольника 0,36 м. Его длина в 2 раза больше ширины. Чему равна площадь прямоугольника?

Решение

Пусть ширина прямоугольника равна х,
тогда его длина равна 2х.
Составим уравнение:
(х + 2х) * 2 = 0,36
3х = 0,36 : 2 = 0,18
х = 0,18 : 3
х = 0,06
Значит, 0,06 м − ширина прямоугольника,
0,06 − 2 = 0,12 (м) − длина прямоугольника.
S = a b = 0,06 * 0,12 = 0,0072 м² - площадь
0,0072 м² = 72 см²
Ответ: 72 см².

Задание 1025

Найдите площадь поверхности и объём прямоугольного параллелепипеда, длина которого равна 12 см, ширина − 7,5 см, а высота − 10 см.

Решение

S = 2 ( a b + а с + b c ) = 2 * (12 * 7,5 + 12 * 10 + 10 * 7,5 ) = 570 (см²) - площадь поверхности
V = a b c = 12 * 10 * 7,5 = 900 (см³) - объем
Ответ: 570 см², 900 см³.

Задание 1026

Ширина прямоугольного параллелепипеда равна а см, длина на 5 см больше ширины, а высота равна 4 см. Составьте выражение для нахождения объёма параллелепипеда.

Решение

V = a * (a + 5) * 4 = 4a * (a + 5).

Задание 1027

Из деревянного бруска, длина которого 8 см, ширина 0,6 дм и высота 4 см, вырезали куб с ребром 0,04 м. Чему равен объём оставшейся части бруска?

Решение

0,6 дм = 6 см; 0,04 м = 4 см.
1)  43 = 64 (см³) - объем куба
2) V = abc = 8 * 6 * 4 = 192 (см³)- объем бруска
3) 192 − 64 = 128 (см³) - объем оставшейся части
Ответ: 128 см³.

Задание 1028

Какой объём занимает вода, налитая в мензурку (рис. 195)? Числа на шкале мензурки означают кубические сантиметры (миллилитры).

Решение

Налито 250 см³ воды.

Задание 1029

Какие из квадратов на рисунке 196 равны?

Решение

Равны между собой внешний квадрат верхнего
рисунка и внешний квадрат нижнего, внутренний квадрат верхнего и внутренний нижнего рисунка.

Задание 1030

Среди фигур, обозначенных буквами, найдите равные фигуры (рис. 197).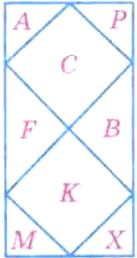

Решение

C = K, A = P = M = X, F = B.

Задание 1031

На рисунке 198 изображён куб. Назовите рёбра верхней и нижней граней, переднюю грань, вершины правой грани, равные рёбра.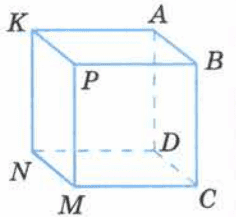

Решение

Ребра верхней грани: АВ, ВР, РК, КА.
Ребра нижней грани: CD, DN, NM, МС.
Передняя грань ВРМС.
Вершины правой грани: А, В, С, D.
Все рёбра куба равны между собой.

Задание 1032

Пятиугольное поле ABCDM, план которого изображён на рисунке 199, разбито на четыре части отрезками АС и ВМ. Назовите эти части и найдите площадь поля, если площади треугольных частей равны 50 тыс. м², 60 тыс. м², 170 тыс. м², а четырёхугольной − 380 тыс. м².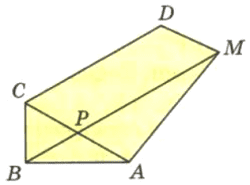

Решение

Поле разбито на части: АВР, СРВ, АРМ, CDMP.
Площадь равна сумме площадей частей поля
S = 50 + 60 + 170 + 380 = 660 тыс. м².

Задание 1033

Дополните каждый треугольник, изображённый на рисунке 200, до прямоугольника и найдите площади треугольников.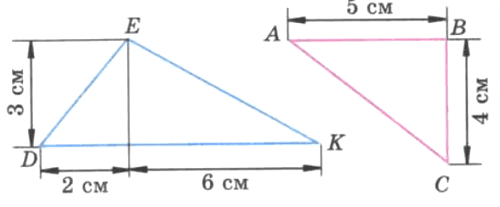

Решение

S DEK = S DMEP * 2 + S PENK : 2 = 3 * 2 : 2 + 6 * 3 : 2 = 12 (см).
S ABC = S ABCF : 2 = 5 * 4 : 2 = 10 (см²).

Задание 1034

Каким свойством обладают точки окружности? Какой отрезок называют радиусом окружности? Диаметром окружности? Начертите окружность и проведите три радиуса этой окружности и её диаметр.

Решение

Точки окружности равноудалены от центра окружности.
Радиус − отрезок, один конец которого находится в центре окружности, а другой лежит на ней.
Диаметр − отрезок проходящий через центр окружности, оба конца которого лежат на ней.

Задание 1035

Начертите окружность и проведите два её радиуса, образующие прямой угол.

Решение

Задание 1036

Начертите окружность с центром О и радиусом 4,7 см. Постройте два отрезка АВ и АС длиной 3 см так, чтобы точки А, В и С лежали на окружности.

Решение

Задание 1037

Запишите все трёхзначные числа, для записи которых используются только цифры 3 и 0.

Решение

300, 330, 303, 333.

Задание 1038

Выполните действия:
а) (246535 − 85897) : 1306;
б) 157464 : (14904 : 23);
в) 1600731 : (5163 − 356);
г) 515453 : (261 924 : 156);
д) (97548 + 69432) : (16400 − 15388);
е) 1067154 : 4807 − 189 + 707 * 390.

Решение

а) (246535 − 85897) : 1306 = 160638 : 1306 = 123

б) 157464 : (14904 : 23) = 157464 : 648 = 243

в) 1600731 : (5163 − 356) = 1600731 : 4807 = 333

г) 515453 : (261924 : 156) = 515453 : 1679 = 307

д) (97548 + 69 432) : (16400 − 15388) = 166980 : 1012 = 165

е)1067154 : 4807 − 189 + 707 * 390 = 222 − 189 + 275730 = 275763

Задание 1039

Составьте выражение и найдите его значение:
а) сумму 369 и 471 разделите на разность 872 и 842;
б) произведение чисел 38 и 48 разделите на сумму 39 и 57.

Решение

а) (369 + 471) : (872 − 842) = 840 : 30 = 28

б) (38 * 48) : (39 + 57) = 1824 : 96 = 19

Задание 1040

Решите уравнение:
а) 13x + 12x + 15 = 240;
б) (14x − 2х) : 17 = 312.

Решение

а) 13x + 12x + 15 = 240
25x = 225
x = 225 : 25
х = 9

б) (14x − 2x) : 17 = 312
12x = 312 * 17 = 5304
x = 5304 : 12
х = 442

Задание 1041

Верно ли неравенство 398 + 24 * 87 < 3100?

Решение

Да, верно: 398 + 24 * 87 = 398 + 2088 = 2486 < 3100.

Задание 1042

Подсчитайте, сколько печатных знаков:
а) на странице, если в ней 40 строк, а в строке 58 знаков (основной шрифт);
б) в строке, если на странице 48 строк, а всего на странице 3360 знаков (петит).

Решение

а) 40 * 58 = 2320 знаков

б) 3360 : 48 = 70 знаков

Задание 1043

Выделите целую часть числа:
а) 347/15;
б) 3271/32;
в) 437/24;
г) 4389/43.

Решение

а) $\frac{347}{15}=23\frac2{15}$

б) $\frac{3271}{32}=102\frac7{32}$

в) $\frac{437}{24}=18\frac5{24}$

г) $\frac{4389}{43}=102\frac3{43}$

Задание 1044

Выполните действия:
а) 7 3/17 + 8 5/17 − 1 6/17;
б) 5 7/10 − ( 4 3/10 − 2 1/10 );
в) 10 7/15 − 3 1/15 + 4 4/15;
г) 9 9/11 − ( 3 2/11 − 2 3/11 ).

Решение

а) $7\frac3{17}+8\frac5{17}-1\frac6{17}=7+8-1+\frac{3+5-6}{17}=14+\frac2{17}=14\frac2{17}$

б) $5\frac7{10}-(4\frac3{10}-2\frac1{10})=5\frac7{10}-2\frac2{10}=3\frac5{10}$

в) $10\frac7{15}-3\frac1{15}+4\frac4{15}=10-3+4+\frac{7-1+4}{15}=11+\frac{10}{15}=11\frac{10}{15}$

г) $9\frac9{11}-(3\frac2{11}-2\frac3{11})=9\frac9{11}-\frac{10}{11}=8\frac{10}{11}$

Задание 1045

Из 15 гусей белыми были 7, а остальные − серыми. Какую часть всех гусей составляли серые гуси?

Решение

15 − 7 = 8 (г.) - серых
Ответ: 8/15 от общего количества гусей.

Задание 1046

Из 18 верблюдов в караване 5 были одногорбыми, а остальные − двугорбыми. Какую часть всех верблюдов каравана составляли двугорбые верблюды?

Решение

18 − 5 = 13 (в.) - двугорбых
Ответ: 13/18.

Задание 1047

Площадь кухни 8 м², что составляет 1/5 площади всей квартиры. Какова площадь квартиры?

Решение

 8 : 1 * 5 = 40 (м²) - площадь всей квартиры
Ответ: 40 м².

Задание 1048

Выразите в метрах и дециметрах: 3 3/10 м ; 1 1/2 м ; 3 2/5 м.

Решение

3 3/10 м = 3 м 3 дм;
1 1/2 м = 1 м 5 дм;
3 2/5 м = 3 м 4 дм.

Задание 1049

Выразите в минутах: 1/5 ч; 3/4 ч; 2 1/2 ч; 5 2/3 ч.

Решение

1/5 ч 60 : 5 = 12 мин;
3/4 ч = 60 : 4 * 3 = 45 мин;
2 1/2 ч = 2 * 60 + 60 : 2 * 1 = 150 мин;
5 2/3 ч = 5 * 60 + 60 : 3 * 2 = 340 мин.

Задание 1050

В одни из суток года продолжительность ночи на 20 мин меньше продолжительности дня. Сколько времени длится день в эти сутки?

Решение

Пусть х − продолжительность дня,
тогда х − 40 − продолжительность ночи.
Составим уравнение:
х + (х − 40) = 24 * 60
2х = 1440 + 40
х = 1480 : 2
х = 740
Значит, продолжительность дня 740 мин.
740 мин = 12 ч 20 мин.

Задание 1051

Начертите координатный луч, приняв за единичный отрезок длину 10 клеток тетради.
Отметьте на этом луче точки: А (0) , В (0,3) , С (0,6) , D (1 1/2) , E (1,2) , М (1) , N (0,2) , K (4/5) , Р (0,8) , T (1 3/5).

Решение

Задание 1052

Сравните числа:
а) 3 001 257 и 3 010 256;
б) 2,57 и 1,837;
в) 0,0005 и 0,003;
г) 0,94 и 0,495;
д) 1 8/17 и 2 1/17;
е) 12/25 и 9/25.

Решение

а) 3 001 257 < 3 010 256

б) 2,57 > 1,837

в) 0,0005 < 0,003

г) 0,94 > 0,495

д) 1 8/17 < 2 1/17

е)12/25 > 9/25

Задание 1053

Из деревни вышел пешеход, а через 2 ч вслед за ним выехал велосипедист. Скорость велосипедиста 10 км/ч, а скорость пешехода 5 км/ч. Через сколько времени после своего выезда велосипедист догонит пешехода?

Решение

Пусть х часов ехал велосипедист,
тогда пешеход шел х + 2 часа:
Составим уравнение:
(х + 2) * 5 = х * 10
5х + 10 = 10x
5х = 10
х = 2
Ответ: через 2 часа.

Задание 1054

Расстояние между двумя поездами, идущими навстречу друг другу, равно 8500 км. Через сколько часов поезда встретятся, если они будут идти без остановок: один со скоростью 80 км/ч, другой − 90 км/ч?

Решение

1) v = 80 + 90 = 170 (км/ч) - скорость сближения двух поездов
2) 8500 : 170 = 50 (ч) - через столько времени встретятся поезда.
Ответ: через 50 часов.

Задание 1055

С одной станции одновременно в противоположных направлениях вышли два поезда. Скорость одного из них 54 км/ч, а скорость другого на 18 км/ч больше. Через сколько часов расстояние между ними будет равно 504 км?

Решение

1) 54 + 54 + 18 = 126 (км/ч) - скорость удаления поездов
2) 504 : 126 = 4 (ч) - через столько времени между поездами будет 504 км
Ответ: через 4 часа.

Задание 1056

Теплоход шёл 2,5 ч по течению реки и 3,2 ч против течения. Какой общий путь прошёл теплоход, если его собственная скорость 22 км/ч, а скорость течения 3 км/ч?

Решение

1) 22 + 3 = 25 (км/ч) - скорость теплохода по течению
2)  22 − 3 = 19 (км/ч) - скорость против течения 
3)  2,5 * 25 + 3,2 * 19 = 123,3 (км) - прошел теплоход
Ответ: 123,3 км.

Задание 1057

Выполните действия:
а) (5124 − 4267) * 23 − 5200 : 325;
б) (13 412 + 124 956) : 46 − 73 * 36;
в) 3,42 : 0,57 * (9,5 − 1,1) : ((4,8 − 1,6) * (3,1 + 0,05));
г) (6,9 − 5,52 : 0,69 * 0,85) * ((5 − 0,125) : (3,7 + 0,05));
д) 1,7 * (3,9658 + 16,0142) − 8,591 : (7,1 − 5,68);
е) 14,1414 : (89,413 − 75,413) + 0,808 * (0,9163 + 0,0837).

Решение

а) (5124 − 4267) * 23 − 5200 : 325 = 857 * 23 − 16 = 19695

б) (13412 + 124956) : 46 − 73 • 36 = 138 368 : 46 − 2628 = 380

в) 3,42 : 0,57 * (9,5 − 1,1) : ((4,8 − 1,6) * (3,1 + 0,05) = 6 * 8,4 : (3,2 * 3,15) = 50,4 : 10,08 = 5

г) (6,9 − 5,52 : 0,69 * 0,85) * ((5 − 0,125) : (3,7 + 0,05)) = (6,9 − 8 * 0,85) * (4,875 : 3,75) = 0,1 * 1,3 = 0,13

д) 1,7 * (3,9658 + 16,0142) − 8,591 : (7,1 − 5,68) = 1,7 * 19,98 − 8,591 : 1,42 = 33,966 − 6,05 = 27,916

е)14,1414 : (89,413 − 75,413) + 0,808 * (0,9163 + 0,0837) = 14,1414 : 14 + 0,808 * 1 = 1,8181

Задание 1058

Упростите выражение:
а) 5а + 12,4 + 2,6 + 3,14 + 1,4а + 0,4а + 2,4;
б) 13,4 + 6 + 5,6 + 8,2b + 7,28 + 1,7b + 2,3.

Решение

а) 5a + 12,4 + 2,6 + 3,14 + 1,4a + 0,4a + 2,4 = 6,8a + 20,54

б) 13,4 + 6 + 5,6 + 8,2b + 7,28 + 1,7b + 2,3 = 9,9b + 34,58

Задание 1059

Найдите значение выражения:
а) 19,1у + 121,4 + 0,9у при у = 48,5;
б) 5,6m + 8,4m + 186,4 при m = 35,5.

Решение

а) 19,1y + 121,4 + 0,9y = 20y + 121,4
при y = 48,5 => 20 * 48,5 + 121,4 = 970 + 121,4 = 1091,4

б) 5,6m + 8,4m + 186,4 = 14m + 186,4
при m = 35,5 => 14 * 35,5 + 186,4 = 497 + 186,4 = 683,4

Задание 1060

В пяти маленьких и двух больших коробках 54 цветных карандаша, а в трёх маленьких и двух больших коробках 42 карандаша. Сколько карандашей в одной маленькой и сколько в одной большой коробке?

Решение

Из условий задачи следует, что 2 маленькие коробки содержат
1) 54 − 42 = 12 (к.) - содержат 2 маленькие коробки
2) 12 : 2 = 6 (к.) - содержит 1 маленькая коробка
3) (42 − 6 * 3) : 2 = (42 − 18) : 2 = 12 (к.) - содержит одна большая коробка
Ответ: 6 и 12 карандашей.

Задание 1061

Длина прямоугольника в 5 раз больше его ширины. Найдите стороны прямоугольника, если его периметр 1212 см.

Решение

Пусть х − ширина прямоугольника,
тогда 5х − его длина.
Составим уравнение:
2 * (х + 5х) = 1212
6х = 1212 : 2 = 606
х = 606 : 6
х = 101
Значит, ширина прямоугольника 101 см,
5 * 101 = 505 (см) - длина прямоугольника 
Ответ: 101 см, 505 см.

Задание 1062

В одной бочке было в 3 раза больше бензина, чем в другой. Когда в первую налили ещё 46 л, а во вторую 18 л, то в двух бочках стало 184 л бензина. Сколько литров бензина было в каждой бочке первоначально?

Решение

Пусть х − количество бензина в первой бочке,
тогда 3х − количество бензина во второй бочке.
Составим уравнение:
(3x + 46) + (х + 18) = 184
4х = 184 − 46 − 18 = 120
х = 120 : 4
х = 30
Значит, объем первой бочки 30 л,
3 * 30 = 90 (л) − объем второй бочки.
Ответ: 30 л, 90 л.

Задание 1063

Площадь земли, засеянной пшеницей, в 6 раз больше площади, засеянной ячменём, а площадь, засеянная рожью, в 3 раза меньше площади, засеянной пшеницей. Сколько гектаров земли засеяно каждой культурой, если рожью засеяно на 120 га больше, чем ячменём?

Решение

Пусть засеяно ячменем − х,
тогда засеяно пшеницей − 6x,
а засеяно рожью − 6х : 3 = 2х.
Составим уравнение:
2х − х = 120
х = 120
Значит, 120 га засеяно ячменём,
2 * 120  = 240 (га) − засеяно рожью,
6 * 120 = 720 (га) − засеяно пшеницей.
Ответ: 120 га, 240 га, 720 га.

Задание 1064

В зрительном зале кинотеатра 16 рядов, и в каждом ряду 24 места. Сколько денег выручит кинотеатр за 3 сеанса, если цена билета m р. и на эти сеансы все билеты будут проданы?

Решение

3 * 16 * 24 * m

Задание 1065

Измерьте углы АОВ, ВОС, DMN, NME (рис. 201). Какие из этих углов равны?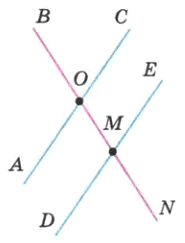

Решение

∠AOB = ∠NME
∠BOC = ∠DMN

Задание 1066

Постройте угол АОВ в 140° и проведите луч ОМ так, чтобы он разделил угол АОВ на два угла, один из которых на 40° больше другого.

Решение

∠AOM − ∠MOB = 40°
∠AOM + ∠MOB = 140°
∠MOB = (140° − 40°) : 2 = 50°
∠AOM = 50°+ 40° = 90°

Задание 1067

Найдите объём прямоугольного параллелепипеда, если его длина 2,3 см, ширина 1,4 см, а высота 0,5 см.

Решение

V = a b c = 2,3 * 1,4 * 0,5 = 1,61 (см³) - объём прямоугольного параллелепипеда
Ответ: 1,61 см³.

Задание 1068

Длина прямоугольного параллелепипеда равна а см, ширина − на 2 см меньше длины, а высота равна 5 см. Составьте выражение для нахождения объёма этого параллелепипеда.

Решение

V = abc = a(a − 2) * 50 = 50a * (a − 2).

Задание 1069

Вычислите в арах площадь участка, изображённого на рисунке 202.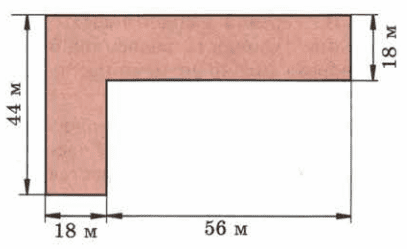

Решение

S = 44 * 18 + 56 * 18 = ( 44 + 56 ) * 18 = 1800 (м²) - площадь участка
1800 м² = 18 a
Ответ: 18 a.

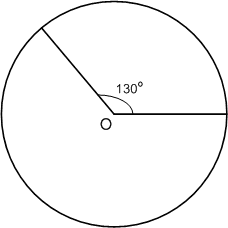
Задание 1070

Начертите окружность и постройте два радиуса этой окружности так, чтобы угол между ними был равен 130°.

Решение

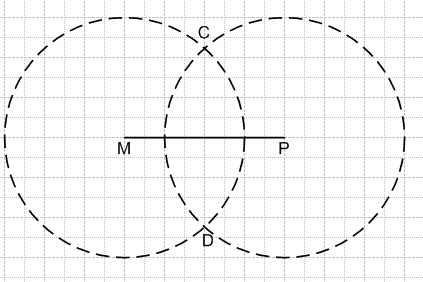
Задание 1071

Начертите отрезок МР, длина которого 4 см, и найдите две точки, удалённые от концов отрезка на 3 см.

Решение

Задание 1072

Расшифруйте надпись на крышке шкатулки, указывающую путь к тайнам математики:

Решение

Терпение и труд.