Ответы к стр. 16

2. На соревнованиях по конькобежному спорту первый спортсмен преодолел дистанцию за 75 с, а второй − на 5 с быстрее. За сколько секунд преодолел дистанцию второй спортсмен?

75 − 5 = 70 (с) − время преодоления дистанции вторым спортсменом.
Ответ: за 70 секунд.

3. Вырази в секундах: 3 мин; 10 мин; 8 мин; 2 мин 3 с; 15 мин 47 с.

3 мин = 3 * 60 с = 180 с
10 мин = 10 * 60 с = 600 с
8 мин = 8 * 60 с = 480 с
2 мин 3 с = 2 * 60 с + 3 с = 123 с
15 мин 47 с = 15 * 60 + 47 с = 947 с

4. За 50 с токарь изготавливает одну деталь. Сколько таких деталей он изготовит за 3 ч, если будет работать с такой же производительностью?

1) 3 ч = 3 * 60 мин = 180 мин = 180 * 60 с = 10800 (с);
х180
    60 
10800
2) 10800 : 50 = 216 (деталей) − изготовит токарь за 3 ч;
_10800 |50  
  100     |216
    _80
      50
    _300
      300
          0
Ответ: 216 деталей.

5. Выполни вычисления.
  45000 − 28529        528 : (800 : 100)    32 * 24 : 48
  21600 − 19054       100 * (534 : 89)     210 * 4 : 14
  420026 + 289870    19 * (780 : 15)       980 : 35 * 28
  108404 + 420296    648 : (816 : 34)       804 : 12 * 14

Решение

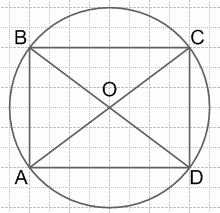
6. Начерти в тетради прямоугольник ABCD (размеры его выбери самостоятельно). Проведи в нем диагонали AC и BD и обозначь точку их пересечения буквой O. Начерти окружность с центром в точке O и радиусом OA. Какой вывод можно сделать?

Вывод: диагонали прямоугольника являются диаметрами окружности, и прямоугольник вписан в окружность.

7. В двух хранилищах было 1000 ц картофеля. Когда из этих хранилищ взяли картофеля поровну, в одном из них осталось 249 ц, а в другом − 187 ц. Сколько центнеров картофеля взяли из каждого хранилища?

1) 249 + 187 = 436 (ц) − картофеля осталось в двух хранилищах
+249
  187
  436

2) 1000 − 436 = 564 (ц) − картофеля всего взяли из хранилищ
_1000
    436
    564

3) 564 : 2 = 282 (ц) − картофеля взяли из каждого хранилища
_564 |2
  4     |282
_16
  16
   _4
     4
     0
Ответ: 282 ц

8. Запиши дроби:
1) одна пятая;
2) две седьмых;
3) четыре девятых;
4) одна шестидесятая;
5) три третьих.

1) 1 − одна пятая
    5
2) 2 − две седьмых
    7
3) 4 − четыре девятых
    9
4) 1 − одна шестидесятая
   60
5) 3 − три третьих
    3

9. Обозначь дробью:
1) закрашенную часть квадрата;
2) незакрашенную часть квадрата.

Закрашенные части
1) 6 − шесть девятых
    9
2) 5 − пять девятых
    9
3) 3 − три девятых
    9
4) 5 − пять девятых
    9

Незакрашенные части
1) 3 − три девятых
    9
2) 4 − четыре девятых
    9
3) 6 − шесть девятых
    9
4) 4 − четыре девятых
    9